Характеристики и критерии качества эконометрических моделей

Выявление лучшего варианта эконометрической модели обычно осуществляется путем сравнения соответствующих им качественных характеристик, которые можно рассчитать на основе исходной статистической информации, содержащейся в векторе у, матрице Х, и новой расчетной информации, появляющейся после построении каждого из вариантов модели. Логика в решении этого вопроса достаточно простая: лучшему варианту модели в общем случае должны соответствовать и лучшие значения характеристик его качества.

Здесь следует отметить, что основным условием высокого качества модели является обоснованность математической формы функционала f (a, x _t), как по составу включенных в него независимых переменных, так и по виду их взаимосвязей с зависимой переменной у_t, в совокупности определяющих причины ее изменчивости. В этой связи, новая информация, появившаяся после построения функционала f (a, x _t), позволяет установить, насколько удалось реализовать это условие на практике.

В общем случае качество эконометрической модели оценивается по двум группам характеристик. В первую из групп включим показатели, критерии, выражающие степень соответствия построенной модели основным закономерностям описываемого ею процесса. Во вторую – показатели и критерии, в большей степени оценивающие точность ее аппроксимации наблюдаемых значений процесса у_t .

В этой связи следует отметить, что к критериям первой группы могут быть отнесен и критерий Стьюдента, используемый для оценки значимости влияния каждого из факторов х_i, i =1,2,..., n, на зависимую переменную у_t .

Ведущая роль при определении характеристик качества эконометрической модели принадлежит ряду ее выборочной ошибки е_t, t =1,2,..., Т. Соответствие эконометрической модели описываемому ею процессу у_t в значительной степени может быть установлено на основе анализа свойств рассчитанного ряда ошибки e_t, t =1,2,..., Т. Если вариант модели верно отражает основные тенденции процесса у_t , то можно ожидать, что значения ошибки в определенной степени случайны, их свойства близки к свойствам процесса «белого шума». Если же тенденция, закономерности процесса у_t учитываются моделью не в полной мере (в модель не включены какие-либо существенные с содержательной точки зрения факторы, выбрана форма функционала f (a, x _t), неадекватная характеру взаимосвязей между рассматриваемыми переменными и т. п.), то в ряду ошибки обычно появляется некоторая закономерность, свидетельствующая об утрате свойства ее случайности. Заметим, что неслучайный характер фактической ошибки модели e_t может быть предопределен и неверно выбранным методом оценки параметров модели.

Среди методов оценки параметров линейных эконометрических моделей наибольшее распространение получили метод максимального правдоподобия, метод наименьших квадратов и метод моментов. Каждый из них используется при вполне определенных исходных предпосылках относительно свойств ошибки модели e_t. Например, классические варианты этих методов используются в предположении, что ошибки совпадают со свойствами процесса «белого шума» (нулевое среднее, конечная дисперсия, отсутствие автокорреляционных связей).

При этом метод максимального правдоподобия предполагает известным закон распределения ошибки. Чаще всего используется предположение о нормальности ее распределения. В этой связи построенная с использованием метода максимального правдоподобия модель будет считаться адекватной рассматриваемому процессу, если свойства фактической ошибки e_t будут не слишком сильно отличаться от предполагаемых свойств ошибки e_t («белого шума» с нормальным распределением).

Метод наименьших квадратов не выдвигает столь жестких требований к закону распределения ошибки. Согласно ему оценки параметров моделей определяются исходя из критерия минимума суммы квадратов ошибки. В такой ситуации модель, построенная с использованием данного метода, будет считаться адекватной рассматриваемым процессам, если ее ошибка по своим свойствам идентична «белому шуму».

Если в отношении ошибки эконометрической модели e_t выдвигаются предположения, что ее свойства отличны от свойств «белого шума», то для оценки параметров модели обычно используются так называемые обобщенные модификации данных методов.

Отличие ошибки модели от «белого шума» может выражаться, например, непостоянством ее дисперсии на различных участках интервала t =1,2,..., Т; наличием взаимосвязи между ее соседними значениями, выражаемыми, например, уравнением следующего вида e_t = b×e_{t– 1}+ x_t, где x_t – новая ошибка, по своим свойствам близкая к процессу «белого шума» и т. п.

Однако на практике для моделей многих типов такие свойства ошибки модели априорно предвидеть обычно не представляется возможным. Их можно установить, только анализируя свойства фактической ошибки e_t, полученной для моделей, оценки коэффициентов которых определены с использованием классических методов оценивания.

Таким образом, наличие или отсутствие свойства случайности в ряду выборочной ошибки модели e_t, t =1,2,..., Т в определенной мереуказывает на соответствие или несоответствие модели описываемому ею процессу у. В том случае, когда ошибка модели неслучайна, может быть рекомендовано уточнить рассматриваемый вариант модели, выбрать более подходящий для данной ситуации метод оценки ее параметров.

Как было отмечено выше, неслучайность ошибки может иметь различный характер. Наиболее часто она выражается наличием автокорреляционной связи между соседними ее значениями, тенденциями, характеризующими изменения их квадратов, т. е. тенденциями в ряду e_t ², t =1,2,..., Т и других ее производных.

Для выявления неслучайности в ряду ошибки модели обычно используют специфические тесты. В качестве примера опишем особенности использования для этих целей достаточно универсального теста (критерия) Дарбина-Уотсона. Он наиболее широко применяется в эконометрических исследованиях вследствие своей простоты, хотя и не обладает существенной эффективностью (достоверностью). Тест Дарбина-Уотсона обычно используется для установления факта наличия автокорреляционной зависимости первого порядка в ряду ошибки e_t, т. е. между соседними ее значениями, e_t и e_{t +1}, t =1,2,..., Т. Обычно соседние значения ошибки связаны более сильной зависимостью, чем значения e_t и e_{t +2}, e_t и e_{t +3} и т. д. Вследствие этого отсутствие автокорреляционной связи между рядами значений выборочной ошибки e_t и e_{t –1}, t =1,2,..., Т –1 позволяет с большой степенью уверенности утверждать, что в ряду истинной ошибки модели e_t отсутствуют вообще какие-либо автокорреляционные взаимосвязи.

Критерий Дарбина-Уотсона (d) находится в пределах 0 £ d £ 4. Значение d = 0 соответствует случаю, когда между рядами e_t и e_{t +1}существует строгая положительная линейная зависимость, т. е. r ₁ = +1, и значение d = 4 соответствует строгой отрицательной связи, r ₁= –1. Если ряды e_t и e_{t +1}независимы, то r ₁= 0 и d = 2.

Точки d = 0; 2; 4 и определяют границы критерия Дарбина-Уотсона, в пределах которых гипотеза о наличии автокорреляции первого порядка в последовательности ошибок либо принимается (в областях близких к 0 или 4), либо отвергается (в области d = 2), либо решение по данному критерию остается неопределенным (в промежутках между отмеченными областями). Иными словами, на отрезке [0,4] выделяются четыре промежуточные точки, таким образом, что 0 £ d ₁ £ d ₂ £ 2 £ d ₃ £ d ₄ £ 4. Если расчетное значение критерия Дарбина-Уотсона находится на отрезках [0, d ₁], [ d ₄,4], то гипотеза о наличии автокорреляции первого порядка в ряду ошибок модели принимается, если расчетное значение d находится в интервале [ d ₂, d ₃], – то отвергается. Значения d, приходящиеся на полуинтервалы [ d ₁, d ₂] и [ d ₃, d ₄], не позволяют сделать однозначного суждения по данной гипотезе. В последнем случае необходимо проводить более глубокий анализ зависимостей между значениями ошибки e_t, t =1,2,..., Т.

Другую группу критериев, в большей степени направленных на выявление степени точности аппроксимации функционалом f (a, x _t) наблюдаемых значений зависимой переменной у_t, образуют широко используемые в статистике и эконометрике коэффициент множественной корреляции R, коэффициент детерминации D, критерий Фишера F.

Общепринятой в статистике мерой точности аппроксимации является дисперсия (в нашем случае дисперсия модели). Однако значение дисперсии не отражает многих существенных аспектов качества модели и, кроме того, оно не очень пригодно для целей содержательного анализа.

Относительность ошибки может рассматриваться в двух аспектах. Во-первых, по отношению к уровню переменной у, а, во-вторых, – к некоторому уже установленному эталону точности. Как раз эти аспекты в большей степени и учитывают указанные критерии и коэффициенты.

Коэффициент множественной корреляции показывает степень приближения расчетных (по построенной модели) значений зависимой переменной 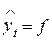(a, x _t) к действительным ее значениям у_t . Величина коэффициента множественной корреляции меняется в пределах от нуля до единицы (0 £ R £ 1). Значения R,близкие к нулю, свидетельствуют о том, что расчетные значения 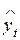плохо аппроксимируют значения у_t. Если R близок к единице, то это означает, что модель хорошо аппроксимирует исходный ряд значений у_t, t =1,2,..., T.

Значения коэффициента детерминации также находятся на отрезке [0,1], 0 £ D £ 1. Его конкретная величина показывает долю изменчивости переменной у, объясняемую включенными в модель факторами х_i, i =1,2,..., n. Например, если D = 0,81, то это означает, что включенные в модель переменные объясняют 81% изменчивости переменной у_t, а остальная ее изменчивость объясняется неучтенными в модели причинами.

Если модель абсолютно точно соответствует исходному ряду зависимой переменной у_t, т. е. расчетные значения 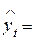f (a, x _t) равны у_t для всех t =1,2,..., T, то D = R = 1.

В тех случаях, когда модель не может ни в какой мере объяснить изменчивость переменной у_t, имеем R = D = 0. При линейной форме зависимости f (a, x _t) это происходит, например, в тех случаях, когда значения у_t равномерно распределяются вокруг линии параллельной оси Х (см. рис.3), что влечет за собой равенство , t =1,2,..., T.

	фактические значения у
		фактические значения у

у у

 

расчетные значения у

х х

а) б)

 

Рисунок. 3. Примеры распределения переменной у_t , при которых линейная эконометрическая модель 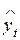= a₀ + a₁ х_1t имеет нулевые коэффициенты детерминации и корреляции

 

Из изложенного выше следует, что высокие значения переменных D и R ассоциируются с хорошей степенью аппроксимации построенной эконометрической моделью 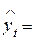f (a, x _t) исходного (заданного) ряда значений зависимой переменной у_t, t =1,2,..., T, а низкие значения – с плохой аппроксимацией.

Вместе с тем следует иметь в виду, что причины плохой аппроксимации могут быть разные. В одних случаях это происходит из-за неверного выбора объясняющих (независимых) переменных, в других – из-за неправильно подобранной формы уравнения модели.

Так, например, если для переменной у_t, фактические значения которой обозначены прерывистой линией на рис.3(а) в качестве эконометрической модели использовать уравнение эллипса 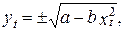а для переменной у_t на рис.3(б) – уравнение синусоиды 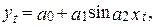то точность описания рассматриваемых процессов была бы значительно выше и характеристики D и R были бы близкими к единице.

Критерий Фишера (F -критерий) также используется для определения надежности всей модели путем сопоставления ее меры ошибки с величиной меры рассеяния переменной у_t относительно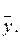

Критерий Фишера может рассматриваться и в качестве меры обоснованности включения в эконометрическую модель всей совокупности независимых переменных. В этом случае его можно отнести и к критериям первой группы, характеризующим степень соответствия построенной модели исследуемому процессу у_t.

Критерий Фишера в такой ситуации рассматривается как своего рода тест при проверке гипотезы, что ни один из независимых факторов не играет никакой роли в объяснении изменчивости переменной у_t или, что то же самое, все коэффициенты при независимых факторах модели равны нулю (a ₁=0, a ₂=0,..., a_п =0).

На практике проверка значимости коэффициентов модели с использованием критерия Фишера состоит в сопоставлении его расчетного значения с табличным значением F _*(п, Т – п –1), соответствующим заданному уровню доверительной вероятности р _* (вероятности ошибки первого рода 1– р _*) и известным степеням свободы п и Т – п –1.

Если оказывается, что F < F _*(п, Т – п –1), то гипотезу о незначимости совокупного влияния независимых факторов на переменную у_t целесообразно принять (вероятность ее осуществления равна р _*). В противном случае роль факторов в объяснении изменчивости переменной у_t следует признать существенной. С ростом F эта роль признается все более значимой.

Критерий Фишера можно использовать и при сравнении качества (точности описания исходного процесса у_t) двух различных альтернативных вариантов модели.

В заключение еще раз обратим внимание на определенные содержательные и количественные взаимосвязи между критериями и показателями качества эконометрической модели различных групп. Например, отметим, что появление автокорреляционных взаимосвязей у значений ошибки, вообще говоря, делает приведенные выше выражения критериев Фишера, коэффициента детерминации, множественных коэффициентов корреляции и т. п. некорректными. Это обусловлено тем, что используемая при расчете их значений сумма квадратов ошибки 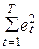не может рассматриваться как мера точности аппроксимации заданного ряда значений у_t, поскольку не учитывает, например, автокорреляционные связи между разновременными ошибками e_t и e_{t + i} , i =1, 2,...

Критерии Стьюдента и Фишера, коэффициенты детерминации и множественной корреляции, отнесенные к разным группам, часто используются совместно при обосновании выбора варианта эконометрической модели. Это связано с тем, что каждый из включенных в модель факторов, как правило, объясняет некоторую долю изменчивости зависимой переменной у_t, пусть даже и небольшую. Вследствие этого, когда независимых факторов не слишком много и между ними не наблюдается сильных взаимосвязей, то исключение из их состава даже малозначимого с точки зрения критерия Стьюдента фактора объективно уменьшает количество информации, объясняющей изменчивость у_t. Это, в свою очередь, влечет за собой уменьшение значений характеристик D, R и F. Может возникнуть такая ситуация, когда, удалив на очередном шаге незначимый фактор, исследователь получает менее удачный по этим показателям вариант модели. Если нет других альтернативных ее вариантов, то возникает проблема выбора между ненадежным вариантом модели со значимыми факторами и более надежным вариантом, у которого некоторые из независимых переменных незначимы. На практике обычно выбор делается в пользу более удачной модели, поскольку более точное описание процесса у_t в эконометрике является и более предпочтительным по сравнению с решением задачи установления перечня значимых по степени влияния на переменную у_t факторов.

Таким образом, этапы формирования модели (обоснование формы функционала, состава независимых переменных) и оценки ее качества в значительной степени взаимосвязаны между собой. Для них, как правило, нельзя установить жесткую очередность. Часто информация, полученная на более поздних этапах, заставляет пересматривать итоги предыдущих. Заметим также, что важную роль на всех этих этапах играет содержательная сторона проблемы. Не подкрепленные результатами содержательного анализа и основанные только на хороших количественных критериях варианты эконометрических моделей часто являются с практической точки зрения бесполезными, бессодержательными аппроксимациями.

Вместе с тем качество модели в значительной степени зависит от того, насколько удачны оценки коэффициентов модели a_i , i =0,1,... п. Они играют, пожалуй, основную роль при обосновании ее качества, поскольку на основе их значений непосредственно определяется одна из важнейших составляющих модели, характеризующих ее качество, – выборочная ошибка.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: