Охарактеризуйте причины изменчивости структуры модели и способы ее отображения в уравнении регрессии.

2. Каковы критерии постоянства и изменчивости структуры?

3. Какие специальные приемы используются для обнаружения изменчивости структуры модели и закономерностей этого процесса с использованием статической и динамической информации?

4. Перечислите типы моделей с переменной структурой.

5. Что собой представляют модели с переключениями?

6. Охарактеризуйте модели с эволюционирующими коэффициентами.

7. В чем состоят особенности оценки коэффициентов моделей с переменной структурой?

Упражнения

Задание 9.1

Компания А, крупный производитель спортивных автомобилей, заинтересована оценить следующую производственную функцию за период 1990–2009 гг.:

где у_t – логарифм среднего выпуска автомобилей в неделю (в тыс. $); х_t – логарифм среднего количества рабочих часов в неделю.

В 2002 г. компания произвела инвестиции в новую производственную технологию. Есть предположение, что это приведет к изменению свободного члена в уравнении (9.1).

Требуется:

1. Модифицировать модель (9.1)

а) с помощью введения фиктивной переменной;

б) с помощью представления ее в виде двух уравнений без фиктивной переменной.

2. Рассчитать вектор оценок параметров модели с фиктивной переменной, если

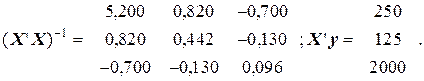
Определить ожидаемые оценки параметров для двух уравнений без фиктивной переменной.

Задание 9.2

Для объяснения переменной “заработная плата” была предложена следующая модель:

где у_t – логарифм совокупной заработной платы; х _{1 t} – количество лет обучения; х _{2 t} – опыт работы; e_t ~(0, s ²).

Выборка составлена таким образом, что номера от 1 до 100 соответствуют женщинам, а со 101 по 300 – мужчинам.

Требуется:

1. Предложить два способа представления нулевой гипотезы, что заработная плата мужчины для данного уровня образования и опыта работы выше, чем у женщины с такими же характеристиками.

2. Проверить гипотезу, что коэффициенты уравнений типа (9.2), построенных отдельно для подвыборок мужчин и женщин, совпадают. Известно, что в модели для женщин сумма квадратов остатков равна 0,13, а для мужчин – 0,33. Оценка МНК по всей выборке дает сумму квадратов остатков 0,6.

3. Предложить способ тестирования гипотезы, что заработная плата зависит от размера фирмы, причем от размеров фирмы линейно зависит коэффициент a _{1 t}:

a _{1 t} = b ₁₀+ b ₁₁ z_t -

4. Показать эквивалентность МНК-оценок коэффициентов a ₁ и a ₂ в модели

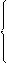где D_t =

и в модели, построенной отдельно для двух подвыборок t =1,..., Т ₁; t = Т ₁+1,..., Т.

 

Задание 9.3

Имеется линейная однофакторная регрессионная модель

в которой неизвестные параметры меняются в случайном порядке

где 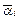– нестохастическая величина и

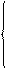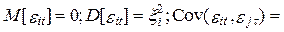
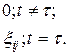
Требуется показать, что эту модель можно интерпретировать как линейную регрессионную модель с гетероскедастичным остаточным членом.

 

Задание 9.4

На основании квартальных данных с 2005 по 2009 гг. с помощью МНК было получено следующее уравнение регрессии:

Регрессионная сумма квадратов равна 112,44, а сумма квадратов остатков – 22,78.

Требуется:

1. Проверить гипотезу о наличии сезонности, если при добавлении в уравнение трех фиктивных переменных, соответствующих трем первым кварталам года, регрессионная сумма увеличилась до 120,75.

2. Проверить гипотезу о наличие структурного изменения между вторым и третьим кварталами 2007 года, если при раздельном проведении двух регрессий на основании данных с первого квартала 2005 г. по 2-й квартал 2007 г. и с 3-го квартала 2007 г. по 4-й квартал 2009 г. были получены суммы квадратов остатков соответственно 11,44 и 2,75.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №10

ТЕМА: ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ СО СПЕЦИФИЧЕСКИМИ ПЕРЕМЕННЫМИ

Краткое содержание темы

Измерение зависимой переменной в дихотомической шкале. Проблемы построения моделей с дискретными зависимыми переменными. Probit-, Logit-, Tobit-модели. Оценивание параметров. Использование нелинейной и линейной регрессионных моделей с гетероскедастичными остатками. Взвешенный МНК.

Примеры моделей с дискретными зависимыми переменными.

 

Вопросы, необходимые для подготовки к проведению занятия

1. Каковы последствия ошибок измерений зависимой переменной?

2. Каковы последствия ошибок измерений независимых переменных?

3. Каковы последствия ошибок измерений и зависимой и независимых переменных?

4. Охарактеризуйте модели с фиктивными независимыми переменными.

5. Дайте классификацию моделей с дискретными зависимыми переменными.

6. В чем состоит суть моделей бинарного выбора?

7. Какие законы распределений наиболее часто используются в моделях бинарного выбора?

8. В чем состоят недостатки линейной модели вероятности?

9. Охарактеризуйте модель бинарного выбора, исходящую из групповых данных?

10. Что собой представляет многомерная probit -модель?

11. Что собой представляют модели множественного выбора?

12. Какие типы моделей используются для описания выбора среди неупорядоченных альтернатив?

13. Каким образом моделируется выбор среди упорядоченных альтернатив?

14. Какие законы распределений используются в моделях счетных данных?

15. Охарактеризуйте последствия построения эконометрической модели на основе усеченной выборки?

16. Как изменяются математическое ожидание и дисперсия зависимой переменной, если при оценки параметров модели используется цензурированная выборка?

17. Охарактеризуйте модели случайно усеченных выборок.

18. Каковы особенности применения метода максимального правдоподобия для оценки параметров моделей с дискретными зависимыми переменными?

19. Как выглядят необходимые условия максимизации логарифма функции правдоподобия для моделей усеченных и цензурированных выборок?

20. Что собой представляет метод максимального счета?

21. В чем суть kernel -метода?

 

Упражнения

Задание 10.1

Logit-модель была применена к выборке, в которой y =1, если количество занятых в фирме выросло (y =0 – в противном случае), х ₁ – доход фирмы, в млн. $; х ₂=1, если фирма относится к области высоких технологий (х ₂=0 – в противном случае). Получена следующая модель:

Требуется определить оценку вероятности роста занятости для фирмы высокотехнологичной фирмы А с доходом в 5 млн. $ и для фирмы Б, не относящейся к сфере высоких технологий и имеющей доход 7 млн. $.

Задание 10.2

Имеется выборка, состоящая из 528 наблюдений, в которой y =1, если заработная плата работника ниже 5$ в час (y =0 – в противном случае). Предполагается, что уровень заработной платы зависит от следующих факторов: х ₁ – образование, лет; х ₂ – пол (1–женский, 0 – мужской); х ₃ – опыт работы, лет. В табл. 10.1 приведены коэффициенты, полученные при оценке линейной регрессии y от х ₁, х ₂ и х ₃ с помощью МНК, и при оценке Logit-модели с помощью нелинейного МНК.

Таблица 10.1

	Коэффициенты
	линейной регрессии	Logit-модели	Выборочные средние
	0,94	5,87
х 1	–0,05	–0,56	13,09
х 2	0,15	1,26	0,46
х 3	–0,01	–0,06	17,66

 

Требуется:

1. Определить на основе Logit-модели, оценку вероятности для мужчины и для женщины, имеющих 12 лет образования и 15 лет опыта работы, оказаться низкооплачиваемыми работниками.

2. Определить на основе Logit-модели, изменение оценки вероятности быть низко оплачиваемым работником для мужчины с характеристиками из п. 1, если он проучится на один год больше.

3. Ответить на вопросы п. 1–2 с использованием линейной регрессионной модели.

 

Задание 10.3

Имеется выборка, состоящая из 528 наблюдений, в которой y =1, если работник состоит в профсоюзе (y =0 – в противном случае). Предполагается, что членство в профсоюзе зависит от следующих факторов: х ₁ – образование, лет; х ₂ – пол (1–женский, 0 – мужской); х ₃ – опыт работы, лет; х ₄ – опыт работы в квадрате. Выборочные средние равны

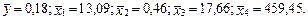
На основе выборочных данных была получена следующая Probit-модель:

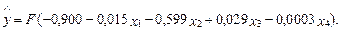
Требуется определить, насколько снижается вероятность быть членом профсоюза в расчете на год дополнительного образования.

 

Задание 10.4

Имеется набор данных, состоящий из 6 наблюдений.

y
x	–1	–2

Требуется:

1. Оценить линейную модель вероятности с помощью МНК. Рассчитать R ².

2. Использовать оцененную модель для разделения индивидуумов на 2 группы. Рассчитать количество случаев правильного отнесения к соответствующей группе, применяя следующее правило классификации:

группа I (y =1), если

группа II (y =0), если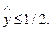

Сопоставьте долю правильного попадания и коэффициент детерминации.

 

Задание 10.5

Среди 48 респондентов был проведен опрос о среднемесячных затратах на табачные изделия. Полученные результаты представлены в табл. 10.2.

Таблица 10.2

 

Требуется:

1. Определить по цензурированным данным МНК-оценку параметра Tobit-модели где e_t ~ N (0, s ²), и у_t = у_t ^*, если у_t ^*>0, у_t =0, если у_t ^*£0.

2. Определить по усеченным на уровне 0 данным МНК-оценку параметра Tobit-модели.

Задание 10.6

В 1973 году в г. Трое (штат Мичиган) проводился референдум по вопросу о введении местного школьного налога. В ходе опроса выявлялись определенные характеристики участников референдума (см. табл. 10.3).

Таблица 10.3

Название характеристики	Значение
PUB1	Один ребенок посещает государственную школу	В противном случае
PUB2	Двое детей посещают государственную школу	В противном случае
PUB3	Трое детей посещают государственную школу	В противном случае
PUB4	Четверо детей посещают государственную школу	В противном случае
PUB5	Пятеро и более детей посещают государственную школу	В противном случае
PRIV	В семье есть дети (один или более), посещающие частную школу	В противном случае
SCHOOL	Респондент работает учителем (в государственной или частной школе)	В противном случае
YESVM	Респондент проголосовал «за» на референдуме по вопросу о введении местного «школьного» налога	В противном случае

 

Кроме того, YEARS = количество лет, прожитых в Трое; LogINC =

= натуральный логарифм годового дохода домашнего хозяйства, $; PTCON = = натуральный логарифм суммы годовых платежей по налогу на имущество, $. Информация о 95 респондентах представлена в табл. 10.4

Таблица 10.4

№	PUB1&2	PUB3&4	PUB5	PRIV	YEARS	SCHOOL	Log INC	PTCON	YESVM
							09.770	7.0475
							10.021	7.0475
							10.021	7.0475
							09.4335	6.3969
							10.021	7.2792
							10.463	7.0475
							10.021	7.0475
							10.021	7.2793
							10.222	7.0475
							09.4335	7.0475
							10.021	7.0475
							09.770	6.3969
							09.770	6.7452
							10.021	7.0475
							10.820	6.7452
							09.770	6.7452
							10.222	7.0475
							10.021	7.0475
							10.222	7.0475
							10.222	6.7452
							10.463	7.0475
							10.222	7.0475
							09.770	6.7452
							10.463	7.2793
							10.021	6.7452
							10.463	7.0475
							09.770	6.7452
							09.770	7.0475
							09.770	6.7452
							10.222	7.0475
							10.021	6.7452
							09.4335	6.7452
							08.294	7.0475
							10.463	7.0475
							10.021	7.0475
							10.222	7.2793
							10.222	7.0475
							10.222	7.4955
							10.021	7.0475
							10.222	7.0475
							10.021	7.0475
							10.820	7.4955
							10.021	7.0475
							10.021	7.0475
							10.021	6.7452
							10.021	7.0475
							09.770	6.7452

 

Продолжение табл. 10.4
							10.222	7.4955
							09.7700	6.7452
							10.021	7.0475
							10.021	6.7452
							09.4335	6.7452
							10.463	7.2793
							09.770	7.0475
							10.021	7.0475
							09.7700	5.9915
							09.4335	7.0475
							09.770	6.3969
							10.021	6.7452
							10.463	7.0475
							10.021	7.0475
							10.820	7.2793
							09.4335	6.7452
							09.770	5.9915
							08.9227	6.3969
							09.4335	7.4955
							09.4335	6.7452
							10.021	7.0475
							10.021	7.0475
							10.021	7.0475
							10.222	7.0475
							09.770	7.0475
							10.021	7.2793
							09.770	7.0475
							09.770	7.0475
							10.222	6.7452
							10.463	6.7452
							10.222	6.7452
							09.770	6.7452
							10.222	7.0475
							10.021	7.2793
							10.463	6.7452
							09.770	7.0475
							10.820	7.4955
							08.9227	5.9915
							09.770	7.0475
							09.4335	6.3969
							09.7700	6.7452
							10.021	7.0475
							10.021	6.7452
							10.222	7.2793
							10.021	7.0475
							10.021	7.0475
							08.9227	5.9915
							10.463	7.4955

Требуется:

1. Оценить параметры следующей модели:

Prob(YESVM=1)= F (PUB1&2, PUB3&4, PUB5, PRIV, YEARS, SCHOOL, LogINC, PTCON)

c использованием МНК, Probit- и Logit-процедур.

2. Рассчитать на основе модели, оцененной с помощью МНК, прогноз вероятности для каждого из респондентов проголосовать “за” введение местного школьного налога. Определить для скольких случаев прогнозное значение выходит за рамки интервала от 0 до 1.

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №11

ТЕМА: МЕТОДЫ ОЦЕНКИ ПАРАМЕТРОВ НЕЛИНЕЙНЫХ ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ

Краткое содержание темы

Причины нелинеаризуемости моделей. Классификация оценки параметров нелинейных моделей. Критерий оценки.

Методы с производными и методы без производных. Построение процедур прямого поиска. Методы Гаусса и представление целевой функции. Процедура оценки коэффициентов модели по методу Гаусса-Зайделя.

Градиентные методы оценки параметров нелинейной модели и представления целевой функции.

Процедуры оценки параметров градиентными методами.

Вопросы, необходимые для подготовки к проведению занятия

1. Каковы причины нелинеаризуемости моделей?

2. По каким признакам классифицируются методы оценки параметров нелинейных моделей?

3. Охарактеризуйте методы с производными и методы без производных?

4. Опишите процедуру прямого поиска.

5. В чем состоит суть методов Гаусса?

6. Опишите градиентные методы оценки параметров нелинейной модели и особенности представления целевой функции.

 

Упражнения

Задание 11.1

Имеется нелинейное однофакторное уравнение регрессии

y=f (x)+ e=a×e^bx + e.

Требуется разложить функцию f (x) в ряд Тейлора второго порядка в точке x ₀ = 0 и определить, чему равен предел разложения в ряд n -го порядка при n®¥?

 

Задание 11.2

Имеется нелинейное однофакторное уравнение регрессии

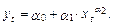
Требуется записать систему нормальных уравнений для определения оценок параметров a ₀, a ₁ и a ₂.

Задание 11.3

Имеется нелинейное уравнение регрессии

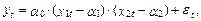
Требуется записать “псевдолинейную” модель.

 

Задание 11.4

Имеется нелинейная однофакторная регрессионная модель

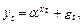
где e_t ~(0, s ²).

Требуется:

1. Вывести рекурсивные формулы для алгоритма Ньютона-Рафсона.

2. Показать, что выполняется следующее равенство:

где S – сумма квадратов остатков.

 

Задание 11.5

Имеется нелинейное однофакторное уравнение регрессии

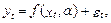
где e_t ~ N (0, s ²).

Требуется показать, что оценка параметра a по методу максимума правдоподобия совпадает с оценкой a, определенной с использованием нелинейного МНК в модели

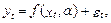
где e_t ~(0, s ²).

 

Задание 11.6

Имеется нелинейное уравнение регрессии

где e_t распределена по закону Коши с функцией плотности f (z)=1/ p (1+ z ²).

Требуется построить алгоритм метода максимального правдоподобия Ньютона-Рафcона.

 

Задание 11.7

В результате оценивания по методу наименьших квадратов получается следующая линейная регрессионная модель:

y_t= 4 x _{1 t}+ 0,5 x _{2 t}+е_t

с ковариационной матрицей

Сov (a)=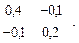

Требуется:

1. Рассчитать значение статистики Вальда для следующих нулевых гипотез:

а) H ₀ : a ₁× a ₂ = 1;

б) H ₀ : ln(a ₁) + ln(a ₂)=0.

Проанализировать взаимоотношения между двумя гипотезами и соответствующими тестами.

2. Написать псевдолинейную модель для оценки приведенной в условии модели в предположении, что верна гипотеза а) из п. 1. Описать, как можно вычислить значение критической статистики в тесте множителей Лагранжа применительно к полученному результату.

3. Вычислить значение статистики в тесте отношения правдоподобия для модели с ограничением, если сумма квадратов остатков в модели без ограничения равна 500, в модели с ограничением – 510, а величина выборки Т =40.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №12

ТЕМА: ИСПОЛЬЗОВАНИЕ ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ В ПРОГНОЗИРОВАНИИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ

Краткое содержание темы

Примеры моделей. Построение прогнозной процедуры и проблема верификации прогноза. Оценка точности прогноза. Доверительный интервал прогноза. Интерпретация параметров модели. Методы оценки доверительного интервала прогноза в моделях с детерминированными и случайными параметрами. Анализ реальных процессов с использованием коэффициентов эластичности.

 

Вопросы, необходимые для подготовки к проведению занятия

1. Что представляет собой “верификации прогноза”?

2. Как оценивается точность прогноза?

3. Что представляет собой “доверительный интервал прогноза”?

4. Охарактеризуйте методы оценки доверительного интервала прогноза в моделях с детерминированными и случайными параметрами.

5. Охарактеризуйте особенности прогнозирования на основе моделей временных рядов.

Упражнения

Задание 12.1

На основании выборки из 20 наблюдений оценено следующее уравнение зависимости затрат на рекламу у от годового оборота х в определенной отрасли (см. задание 2.2):

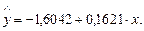
Известно, что ошибка уравнения распределена нормально с нулевым математическим ожиданием и постоянной дисперсией.

Требуется:

1. Определить 95%-й прогнозный интервал математического ожидания целевой переменной y ₀ при x ₀=30.

2. Определить 95%-е прогнозные интервалы математического ожидания целевой переменной при значениях объясняющей переменной 10, 15, 20, 25. Отобразить все прогнозные интервалы и линию регрессии на графике. Прокомментировать результат. Проверить правильность утверждения: “С доверительной вероятностью 95% все перечисленные прогнозные значения математического ожидания лежат в данном интервале ”.

3. Оценить 95%-й прогнозный интервал для отдельного значения целевой переменной при x ₀=30 и сравнить его с прогнозным интервалом в п. 1.

 

Задание 12.2

На основании выборки из 10 наблюдений оценено следующее уравнение зависимости спроса на некоторое благо у домохозяйств определенной структуры (у) от цены этого блага (х ₁) и дохода домохозяйства (х ₂) (см. задание 2.8):

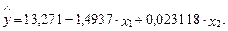
Известно, что ошибка уравнения распределена нормально с нулевым математическим ожиданием и постоянной дисперсией.

Требуется:

1. Рассчитать 95%-й прогнозный интервал математического ожидания целевой переменной y ₀ для значений объясняющих переменных (5,5; 1100) и (6,0; 1150).

2. Определить 95%-й прогнозный интервал для отдельного значения целевой переменной при таких же, как в п. 1, значениях объясняющих переменных.

Задание 12.3

Имеется информация о средних транспортных индексах в летний период 2009 г. (см. табл. 6.2).

Требуется на основе модели ARIMA (0,1,1), оцененной в задании 6.4, построить точечный прогноз исследуемого показателя на 3 периода вперед.

Задание 12.4

Имеются данные процесса контроля качества (см. табл. 6.3).

Требуется на основании модели ARIMA (1,1,1), оцененной в задании 6.5 п. 2, построить точечный прогноз исследуемого показателя на 3 периода вперед.

 

Задание 12.5

Имеется модель следующая модель GARCH(1,1):

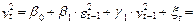
Требуется построить точечный прогноз условной дисперсии на 3 периода вперед, если последнее ее расчетное значение для базисного периода равно 0,7619, а остаток составляет 0,0707.

Задание 12.6

На основании информации, приведенной в табл. 12.1, оценены коэффициенты структурной формы системы взаимозависимых уравнений

С_t =41,4245+0,6216× Y_t + е_t;

Y_t = С_t + I_t.

Требуется:

1. Оценить коэффициенты прогнозной формы.

2. Рассчитать точечный прогноз валового национального продукта и потребления, если объем инвестиций равен 164,50.

3. Построить 95%-й совместный прогнозный интервал для эндогенных переменных.

4. Определить 95%-е прогнозные интервалы для отдельно взятых эндогенных переменных.

Таблица 12.1

Период	Потребление, Сt	Валовый национальный продукт, Yt	Инвестиции, It
	226,37	308,599	95,12
	239,93	327,563	101,29
	252,99	344,420	104,04
	260,37	352,998	102,85
	273,34	378,819	112,39
	292,11	401,523	118,77
	300,62	411,201	120,35
	303,63	406,023	112,61
	317,39	442,000	116,60
	342,41	477,637	129,28
	367,55	533,110	143,03
	386,80	562,388	154,18
	402,24	583,098	161,12
	412,48	609,915	161,64
	413,79	611,528	140,35
	425,93	600,410	133,98
	441,68	628,388	143,25
	445,50	643,152	151,46

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ТИПОВЫЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ОСНОВНЫМ РАЗДЕЛАМ КУРСА

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: