 |
Ошибки выборочного наблюдения
|
|
|
|
Между характеристиками выборочной совокупности и искомыми параметрами генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой.
Общая величина возможной ошибки выборки слагается из ошибок двоякого рода:
- ошибки регистрации;
- ошибки репрезентативности.
Ошибки регистрации свойственны всякому статистическому наблюдению и их появление может быть вызвано несовершенством измерительных приборов, недостаточной квалификацией наблюдателя, недостаточной точностью подсчетов и т.п. Можно полагать, что по сравнению со силошными наблюдениями опасность возникновения ошибок регистрации при выборочном наблюдении должна быть меньше, так как они проводятся более квалифицированными работниками.
Значительно уменьшается при выборочном наблюдении и опасность преднамеренных искажений данных, так как специально подобранные и обученные наблюдатели в них не заинтересованы.
Ошибками репрезентативности называют расхождения между средними величинами или долями признака выборочной и генеральной совокупности. Они присущи только несплошным наблюдениям. Ошибки репрезентативности могут быть:
- систематическими;
- случайными.
Систематическими называются ошибки, которые возникают из-за нарушения научного принципа отбора единиц в выборочную совокупность. Они возникают в тех случаях, когда в результате непрпавильного отбора в выборочную совокупность попали наилучшие или наихудшие единицы.
В результате такого отбора средние и относительные показатели, полученные по выборочной совокупности, будут искаженно характеризовать генеральную совокупность.
Случайные ошибки репрезентативности – это неточности, которые возникают из-за того, что выборочная совокупность не совсем правильно отражает средние величины и величины доли признака генеральной совокупности. Такие ошибки возникают даже при самом строгом соблюдении принципов и правил отбора единиц в выборочную совокупность.
|
|
|
Ошибки репрезентативности свойственны только выборочному наблюдению. Они не могут быть полностью устранены, но они могут быть доведены до незначительных размеров, если соответствующим образом организовать отбор единиц в выборочную совокупность.
Пределы ошибок репрезентативности можно определить с достаточной степенью точности на основании ряда теорем в теории вероятности и математической статистике.
Исключительно важную роль для обоснования и применения выборочного наблюдения играет закон больших чисел. Использование законы больших чисел состоит в том, что при определенных условиях и при достаточно большом объеме наблюдений сводные характеристики, полученные на основе выборочного наблюдения, будут мало отличаться от соответствующих характеристик генеральной доверенности. Основываясь на этом, можно, увеличивая объем выборочной совокупности, уменьшить пределы возможных ошибок репрезентативности, довести их до наименьших размеров. С другой стороны, зная пределы ошибок репрезентативности, можно определить необходимую численность выборочной совокупности.
В статистике особое внимание уделяют ошибке выборочной средней и ошибке выборочной доли.
Ошибка выборочной средней представляет собой расхождение (разность) между выборочной средней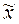 
и генеральной средней 
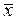, возникающее вследствие несплошного выборочного характера наблюдения. Величина ошибки выборочной средней определяется как предел отклонения 
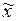от 
, гарантируемый с заданной вероятностью:
где t – гарантийный коэффициент (коэффициент доверия), зависящий от вероятности P, с которой гарантируется невыход разности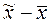 
за пределы 
;
|
|
|
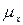– средняя ошибка выборочной средней.
Ошибка выборочной доли представляет собой расхождение (разность) между долей в выборочной совокупности (w) и долей в генеральной совокупности (W), возникающее вследствие несплошного характера наблюдения. Величина ошибки выборочной доли определяется как предел отклонения w от W, гарантируемый с заданной вероятностью:
где t – гарантийный коэффициент, зависящий от вероятности P, с которой гарантируется невыход разности w –W за пределы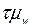 
;
– средняя ошибка выборочной доли.
Значения гарантийного коэффициента t и соответствующие им вероятности P приведены в табл.2. Обычно вероятность принимается равной 0,9545 или 0,9973, а t при этом равно соответственно 2 и 3.
Таблица 2 – Значения гарантийного коэффициента t
| t | P | t | P | t | P |
| 1,00 1,10 1,20 1,30 1,40 1,50 1,60 | 0,6827 0,7287 0,7699 0,8064 0,8385 0,8664 0,8904 | 1,70 1,80 1,90 2,00 2,10 2,20 2,30 | 0,9109 0,9281 0,9426 0,9545 0,9643 0,9722 0,9786 | 2,40 2,50 2,60 2,70 2,80 2,90 3,00 | 0,9836 0,9876 0,9907 0,9931 0,9949 0,9963 0,9973 |
Формулы расчета средней ошибки выборочной средней для различных, наиболее часто используемых способов отбора выборочной совокупности приведены в табл. 3.
Таблица 3 – Формулы расчета средних ошибок выборочной доли и выборочной средней
| Метод отбора выборки | Средняя ошибка | |
| выборочной доли | выборочной средней | |
| Механический или собственно–случайный повторный отбор | 
| 
|
| Механический или собственно–случайный бесповторный отбор | 
| 
|
| Серийный отбор при повторном отборе равновеликих серий | 
| 
|
| Серийный отбор при бесповторном отборе равновеликих серий | 
| 
|
| Типический отбор при повторном случайном отборе внутри групп, пропорциональном объему групп | 
| 
|
| Типический отбор при бесповторном случайном отборе внутри групп, пропорциональном объему групп |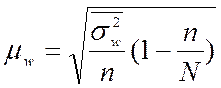 
| 
|
где N – численность генеральной совокупности;
– межсерийная дисперсия выборочной доли;
r – число отобранных серий;
R – число серий в генеральной совокупности;
– средняя из групповых дисперсий выборочной доли;
– дисперсия признака x в выборке;
– межсерийная дисперсия выборочных средних;
– средняя из групповых дисперсий выборочной средней.
|
|
|
|
|
|
