Главная | Обратная связь | Поможем написать вашу работу!

Распространение результатов выборочного наблюдения на генеральную совокупность

Характеристика генеральной совокупности на основе выборочных результатов – это конечная цель выборочного наблюдения.

Выборочный метод применяется для получения характеристик генеральной совокупности по определенным показателям выборки. В зависимости от целей исследования это осуществляется прямым пересчетом показателей выборки для генеральной совокупности или методом расчета поправочных коэффициентов.

Способ прямого пересчета в том, что при нем показатели выборочной доли W или средней х распространяются на генеральную совокупность с учетом ошибки выборки.

Возможная граница генеральной средней определяется по формуле:

где - выборочная средняя;

t – коэффициент доверия;

средняя ошибка выборочной средней.

Возможная граница генеральной доли определяется по формуле:

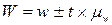
где w – выборочная доля (удельный вес единиц в выборке, обладающих исследуемым признаком; w = m/n);

средняя ошибка выборочной доли.

Способ поправочных коэффициентов применяется, когда целью выборочного метода является уточнение результатов сплошного учета. Данный способ используется при уточнении данных ежегодных переписей скота у населения.

Определение необходимой численности выборки

Одной из наиболее важных и ответственных задач при организации и проведении выборочного наблюдения является установление необходимой численности выборочной совокупности, т.е. такой ее численности, которая обеспечивала бы получение данных, достаточно правильно отражающих изучаемые свойства генеральной совокупности.

При этом должно быть учтено: 1) с какой степенью точности следует получить предельную ошибку выборки; 2) какова должна быть вероятность того, что будет обеспечена обусловленная точность результатов выборочного наблюдения; 3) степень колеблемости изучаемых свойств в исследуемой генеральной совокупности.

Это значит, что необходимая численность выборки (n) устанавливается в зависимости от размеров предельной ошибки выборки (D), от величины коэффициента доверия (t) и от размеров величины дисперсии (s²).

Сами формулы необходимой численности выборки выводятся из формул предельной ошибки выборки следующим образом:

При повторном отборе:

А) для средней

в формуле предельной ошибки выборки

D = t

обе ее стороны возводим в квадрат

D² = t²

Откуда

D² =

и затем

n = .

Таким образом, необходимая численность выборочной совокупности равна произведению квадрата коэффициента доверия и дисперсии признака, деленному на квадрат предельной ошибки выборки.

б) для доли:

в формуле предельной ошибки выборки:

D = t ;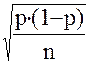

обе ее стороны возводим в квадрат и получим:

D² = t²

откуда

D² =

и затем

n = .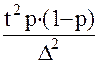

Таким образом, в этом случае необходимая численность выборочной совокупности равна произведению квадрата коэффициента доверия и дисперсии доли, деленному на квадрат предельной ошибки выборки.

При бесповторном отборе:

А) для средней

в формуле предельной ошибки выборки

D = t ,

после ряда преобразований получаем:

n = ;

б) для доли:

из формулы предельной ошибки выборки:

D = t ;

после ряда преобразований получаем:

n = .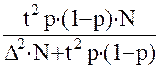

Аналогичным образом определяются объемы выборок при различных способах отбора выборочной совокупности. Для серийного отбора определяется число отобранных серий. Формулы расчета приведены в табл. 4.

Таблица 4 – Формулы расчета объема выборки

Метод отбора выборки	Объем выборки или число серий для определения
выборочной доли	выборочной средней
Механический и собственно-случайный повторный отбор
Механический и собственно-случайный бесповторный отбор
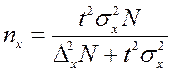
Серийный отбор при повторном отборе равновеликих серий
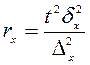
Серийный отбор при бесповторном отборе равновеликих серий
Типический отбор при повторном случайном отборе внутри групп, пропорциональном объему групп
Типический отбор при бесповторном случайном отборе внутри групп, пропорциональ-ном объему групп

где n_w, n_x – объемы выборок соответственно для определения ошибок выборочной доли и выборочной средней;

r_w, r_x – число отобранных серий соответственно для определения ошибок выборочной доли и выборочной средней;

– предельные ошибки соответственно выборочной доли и выборочной средней.

Примеры решения заданий

Задача 1

Был произведен 20%-й механический отбор вагонов с целью определения доли полувагонов в общей численности вагонного парка и cредней массы отправки нетто.

Порядковый номер	Род вагона	Принадлежность собственнику	Масса отправки, кг
	платформа	РЖД
	полувагон	ПГК
	платформа	РЖД
	крытый	РЖД
	полувагон	РЖД
	полувагон	РЖД
	изотермический	Рефсервис
	крытый	РЖД
	платформа	РЖД
	платформа	РЖД

Рассчитайте:

- ошибку выборки с вероятностью 0,683 для доли полувагонов и 0,954 для средней массы отправки нетто (массу отправки выразите в тоннах);

- определите пределы генеральной доли и генеральной средней.

Произведите расчет необходимой численности выборки для определения средней массы отправки, чтобы можно было гарантировать ошибку выборки, не превышающую 5,8 т.

Решение: Доля полувагонов в выборке:

3 полувагонов / 10 вагонов * 100 = 30%

Cредняя массы отправки нетто:

(53100 + 69200 + 50900 + 53650 + 62700 + 67500 + 32500 + 53800 + 47200 + 51300) / 10 = 54185 кг

Расчет предельной ошибки бесповторной случайной выборки:

1) предельная ошибка для средней:

2) предельная ошибка для доли

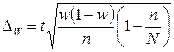
N – объем генеральной совокупности (50);

n – объем выборочной совокупности (10);

- средняя в генеральной совокупности;

- средняя в выборочной совокупности (54185 кг);

р – доля единиц в генеральной совокупности;

w – доля единиц в выборочной совокупности (30%);

S² - выборочная дисперсия.

Определим предельную ошибку для доли с вероятностью 0,683 (т.е. t = 1):

Доверительные интервалы для генеральной доли устанавливаются на основе соотношений:

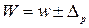
30 – 12,96 ≤ р ≤ 30 + 12,96

17,04% ≤ р ≤ 42,96%

Таким образом, доля полувагонов в генеральной совокупности будет изменяться от 17,04% до 42,96%. В генеральной совокупности доля полувагонов составляет 28%. Таким образом, полученные результаты достоверны.

Определим предельную ошибку для средней отправки нетто (с вероятностью 0,954, т.е.t = 2). Но на начальном этапе рассчитаем выборочную дисперсию:

Порядковый номер	Масса отправки, кг (xi)	(xi – xcp)²










Итого

Xcp = 54185 кг

Дисперсия будет равна:

кг или 5,699 тонн

Доверительные интервалы для генеральной средней можно установить на основе соотношений

где 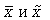– генеральная и выборочная средние соответственно;

– предельная ошибка выборочной средней.

54185 – 5699 ≤ ≤ 54185 + 5699

48486 ≤ ≤ 59884

Средняя масса погрузки нетто в генеральной совокупности изменяется в пределах от 48486 кг до 59884 кг с вероятностью 95,4%.

Средняя масса погрузки нетто в генеральной совокупности составила 53442 кг.

Чтобы рассчитать численность бесповторной простой случайной выборки, можно использовать следующие формулы (для средней при бесповторном способе):

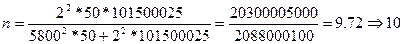
Численности выборки для определения средней массы отправки, чтобы можно было гарантировать ошибку выборки, не превышающую 5,8 т, должна составлять 10 единиц.

Задача 2

Определить ошибку выборки (типический способ отбора) и определить необходимый объем выборки при заданной t.

В цехе работает 450 человек. Для обследования работников по производительности труда взято 84 человека. Результаты представлены в таблице.

Производительность труда, деталей в час	Количество работников, ед.
Смена №1	Смена №2
До 20
20-25
25-30
30-35
35-40
Более 40

Заданная вероятность Р=0,9935, относительная ошибка выборки 2,1%.

Решение:

Типическая (стратифицированная) выборка предполагает разделение неоднородной генеральной совокупности на типологические или районированные группы по какому-либо существенному признаку, после чего из каждой группы производится случайный отбор единиц. Для типической выборки величина стандартной ошибки зависит от точности определения групповых средних.

Если место повторный отбор, то предельная ошибка типической выборки рассчитывается по следующей формуле:

где t – коэффициент доверия (при Р=0,9935 коэффициент доверия равен 2,75).

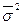- средняя из групповых дисперсий;

n – объем выборочной совокупности.

Объем выборки при типическом способе отбора (повторный) определяется по формуле:

Если место бесповторный отбор, то предельная ошибка типической выборки рассчитывается по следующей формуле:

где N – объем генеральной совокупности.

Объем выборки при типическом способе отбора (бесповторный) определяется по формуле:

Относительная ошибка выборки определяется по формуле:

где - относительная предельная ошибка выборки;

- предельная ошибка для среднего значения;

- генеральная средняя.

Пусть в данном случае речь идет о бесповторном типическом отборе.

На начальном этапе определим среднюю из групповых дисперсий:

где f_i – частота;

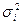- групповая дисперсия.

Групповая дисперсия определяется по следующей формуле:

где x_i – значение признака;

- среднее значение признака в группе.

В данном случае необходимо вычислить среднюю интервального ряда. Поэтому в качестве значения признаков в группах принимаются середины интервалов (простая средняя между верхней и нижней границей каждого интервала), в результате чего образуется дискретный ряд.

Если имеются интервалы с открытыми границами (в данной задаче это первый и последний интервал), то для расчета средней в этих условиях условно определяют неизвестную границу интервала. Обычно в этих условиях берут значение последующего интервала (для первого) или предыдущего (для последнего).

С учетом этих замечаний рассчитаем среднюю оценку по формуле средней арифметической взвешенной (т.к. каждое значение признака в исследуемой совокупности встречается неодинаковое число раз)

, где

Для расчета средней величины производительности труда по сменам и дисперсии в вспомогательной таблице.

Производительность труда, деталей в час	Х_i	Количество работников, ед.
Смена №1	Смена №2
f_i	x_i*f_i	(x_i-x_ср)²*f_i	f_i	x_i*f_i	(x_i-x_ср)²*f_i
До 20	17,5		17,5	172,266			268,698
20-25	22,5		112,5	330,078		157,5	304,081
25-30	27,5		412,5	146,484			45,558
30-35	32,5			35,156			116,219
35-40	37,5		187,5	236,328			424,277
Более 40	42,5			564,063		42,5	179,804
ИТОГО	-			1484,375			1338,636
Среднее	-	1225 / 40 = 30,625	1280 / 44 = 29,091
Дисперсия	-	1484,375 / 40 = 37,109	1338,636 / 44 = 30,424

Средняя из групповых дисперсий составит

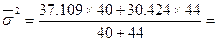33,607.

Тогда предельная ошибка типической выборки составит:

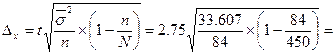1,569.

Определим необходимый объем выборки, чтобы относительная ошибка выборки была равна 2,1%.

При точечной оценке генеральная средняя будет совпадать с выборочной средней и составит:

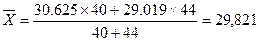
Тогда предельная ошибка составит:

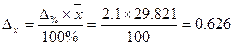
Объем выборки при типическом способе отбора (бесповторный) составит:

Вывод: ошибка выборки (типический способ отбора, бесповторный) составит 1,596.

Чтобы относительная ошибка выборки составляла только 2,1% необходимо обследовать 266 работников.

Задача 3

Методом собственно-случайного бесповторного отбора из общей численности заемщиков банка (5 тыс. чел.) было отобрано 500. Установлено, что 20% заемщиков в выборке старше 60 лет.

Определить с вероятностью 0,683 пределы, в которых находится доля заемщиков банка в возрасте старше 60 лет.

Решение:

Средняя ошибка выборочной доли заемщиков старше 60 лет определяется следующим образом:

С вероятностью 0,683 (гарантийный коэффициент t=1) предельная ошибка выборочной доли работников старше 60-ти лет составит

Верхняя граница генеральной доли

Нижняя граница генеральной доли

С вероятностью 0,683 можно утверждать, что доля заемщиков в возрасте старше 60 лет на предприятии колеблется от 18,3% до 21,7%.

Задача 4

В районе проживает 2000 семей. Предполагается определить средний размер семьи в районе по выборке, взятой методом механического (или собственно-случайного) бесповторного отбора. При этом с вероятностью 0,997 ошибка среднего размера семьи в выборке (выборочной средней) не должна превышать 0,8 человека при среднем квадратическом отклонении в размере семьи 2 человека.

Определить необходимую численность выборки для определения среднего размера семьи в районе.

Решение:

Необходимая численность выборки при вероятности 0,997 (гарантийный коэффициент t=3) определяется следующим образом:

семей.

Задача 5

В трех районах 30 тыс. семей. В первом районе - 15 тыс.; во втором - 12 тыс. и в третьем - 3 тыс. семей. Для определения числа детей в семье была проведена 10%-я типическая выборка с отбором единиц пропорционально численности единиц типических групп. Внутри групп применялся метод случайного бесповторного отбора. Результаты выборочного обследования семей в трех районах представлены в таблице

Номер района	Число семей в районе	Среднее число детей в семье	Среднее квадратическое отклонение
		1,3 1,8 0,8	1,2 2,5 0,5

С вероятностью 0,997 определить предел, в котором находится среднее число детей в семье в трех районах.

Решение:

Средняя ошибка выборочной средней при типическом бесповторном отборе определяется следующим образом:

где – средняя из групповых дисперсий выборочной средней;

n – численность выборочной совокупности по всем типическим группам (районам);

N – численность генеральной совокупности (число семей всего).

Объем выборки в каждой типической группе (районе) n_j

где N_j - число семей в j - м районе;

Число семей, выбранных для обследования в каждом районе при условии, что численность выборочной совокупности n по трем районам равна 3000 семей

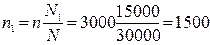семей;

семей.

Среднее число детей в семье по трем районам в выборочной совокупности (выборочная средняя) с учетом численности отобранных групп

чел.

Средняя из групповых дисперсий (внутригрупповая дисперсия)

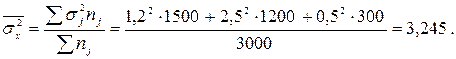
Средняя ошибка выборочной средней при типической выборке (средняя ошибка среднего числа детей в семье)

чел.

Предельная ошибка средней с вероятностью 0,997 (гарантийный коэффициент3) составит

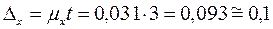чел.

С вероятностью 0,997 можно утверждать, что в трех районах среднее число детей в семье находится в пределах

Вопросы для самопроверки

1. Охарактеризуйте выборочное наблюдение: его достоинства и недостатки.

2. В чем заключается закон больших чисел?

3. Перечислите этапы выборочного наблюдения.

2. Перечислите основные виды отбора и дайте их характеристику.

3. Почему в результате выборочного наблюдения возникают ошибки? Назовите основные виды ошибок.

4. Что такое ошибка выборочной доли и выборочной средней?

5. Охарактеризуйте методику расчета ошибок выборочного наблюдения.

6. Как определить необходимый объем выборки?

7. Как перенести результаты выборочного наблюдения на генеральную совокупность?

⇐ Предыдущая 1 23

Воспользуйтесь поиском по сайту: