 |
Запись действий с отрицательными числами:
|
|
|
|
пр: 
расставляем порядок действий
остались знаки «-», не занятые под действия, они относятся к отрицательным числам;
при выполнении действий, сначала записываем знак результата, потом вычисляем его абсол. величину
1) 
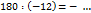
| действие записывается «в строчку», а ниже столбик с положительными числами |
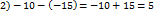
(p – целое, q - натуральное)
десятичная дробь − запись числа в десятичной системе с дробной частью после запятой
пр: 
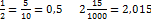действия с десятичными дробями:
| запятая под запятой |
| количество цифр после запятой складывается |
| сдвигаем запятые, чтобы получить целый делитель; при переходе через запятую в делимом -ставим запятую в результат; дописываем нужное количество нулей после запятой |
сдвинуть запятую на n позиций вправо
сдвинуть запятую на n позиций влево
пр: 
перевод обыкновенной дроби в десятичную:
привести знаменатель дроби к круглому числу
пр: 
или разделить числитель на знаменатель «столбиком», получится конечная или бесконечная периодическая десятичная дробь
| пр: | 
| 
«ноль целых сорок пять в периоде»
|
перевод десятичной дроби в обыкновенную:
знаменатель определяется количеством цифр после запятой
пр: 
способ для периодических дробей:
пр: 
пусть 
, тогда
чтобы перенести запятую в конец периода, нужно  , а чтобы перенести запятую в начало периода, нужно  ; вычтем из первого второе
| 
|
, то подчеркнутую цифру увеличиваем на 1 (если была подчеркнута цифра 9, то заменяем ее на 0, а 1 добавляем в разряд слева); все цифры справа заменяем нулями
пр: округлить 195,(18)
| до десятых | 195, 1 818… ≈ 195,2 |
| до десятков | 1 9 5,1818… ≈ 200 |
| до 5-ти значащих цифр | 195,18 18… ≈ 195,18 |
приближенные вычисления:
|
|
|
округляем все числа до заданной точности; выполняем действие; результат округляем
иррациональные числа - числа, которые невозможно представить в виде обыкновенной дроби (это бесконечные непериодические десятичные дроби)
пр: число “пи” 
(это отношение длины окружности к ее диаметру - одинаково для всех окружностей) 
длина окружности: 
площадь круга: 
расстояние между точками равно разнице между координатами правой и левой точки
пр: 
координатная плоскость состоит из двух координатных осей, расположенных под прямым углом, с общим началом отсчета
| ось x - ось абсцисс ось y - ось ординат оси делят плоскость на четыре «четверти» координаты точки - в скобках (сначала по оси x, потом по оси y) |
пр: разделить отрезок в отношении 2: 3: 1
разделим отрезок на 2+3+1=6 частей
и распределим их на три «порции» - из 2 частей, из 3 частей, из 1 части
получим
пр: разделить число 450 в отношении 4: 5
обозначим за x одну часть; нужно разделить число 450 на две «порции» - из 4 частей 
и из 5 частей 
свойство пропорции: 
Две величины прямо пропорциональны, если при увеличении одной величины, вторая величина увеличивается во столько же раз.
пр: на 6 м забора нужно 3 банки краски, сколько краски нужно на 5 м забора?
| ↓↓ |
составим пропорцию (прямую):
|
|
|
Две величины обратно пропорциональны, если при увеличении одной величины, вторая величина уменьшается во столько же раз.
пр: 6 рабочих покрасят забор за 3 ч, за сколько часов покрасят забор 5 рабочих?
| ↓↑ |
составим пропорцию (обратную):
» перед буквой или скобкой можно пропустить
пр: 
упрощение выражений:
- раскрытие скобок
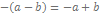
от y
(отнимем 3 слева и справа)
т.е. «слагаемое» можно перенести из одной части уравнения в другую, изменив знак на противоположный
- левую и правую части уравнения можно умножить или разделить на одно число
пр: 
(разделим на 3 слева и справа)
чтобы решить уравнение, нужно привести его к виду: 
уравнение не имеет корней, т.е. не может быть верным равенством «ни при каком x»
уравнение имеет бесконечно много корней, т.е. «верно при любом x»
p % от 
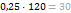
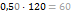
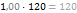
умножить на 1,1
(р)
задачи на части