 |
Порядок выполнения лабораторной работы
|
|
|
|
Описание лабораторной установки
В лабораторной работе используется одноканальный электрокардиограф с тепловой записью. Внешний вид прибора изображен на рис.1, а структурная схема на рис.2.



Биоэлектрические сигналы через кабель отведений и переключатель отведений (ПО) подаются на вход усилителя напряжения (УН). Ко входу усилителя напряжения подключается также источник калибровочного напряжения (ИК). Усиленный сигнал с выхода усилителя напряжения подается на вход усилителя мощности (УМ), после которого сигнал поступает на электромеханический преобразователь (ПЭМ), осуществляющий преобразование электрического сигнала в перемещение теплового пера. Теплочувствительная бумага движется равномерно относительно пера с помощью лентопротяжного механизма (ЛПМ). Для питания усилителя биопотенциалов, электродвигателя лентопротяжного механизма, теплового пера в приборе имеется блок питания (БП).
Органы управления прибором даны на рис.1: сетевой выключатель 1, переключатель чувствительности 2, кнопки переключателя скорости движения ленты 3, кнопка калибровки «1мВ» 4, кнопка успокоения «0» 5, кнопки переключателя отведений 6, разъем для подключения кабеля отведений 7, регулятор смещения пера 8.
Для снятия электрокардиограммы электроды накладываются на пациента по системе стандартных отведений на внутренние поверхности предплечий и голеней. Для лучшего контакта электрода с кожей между ними помещаются марлевые салфетки, смоченные 10%-м водным раствором поваренной соли. Провода кабеля отведений соединяются с электродами в порядке, соответствующем рисунку на лицевой панели кардиографа 9.
Выполнение измерений
|
|
|
1. Закрепите электроды на конечностях студента при помощи резиновых лент и кнопок.
2. Соедините провода отведений с электродами, наложенными на студента.
3. Заземлите электрокардиограф.
4. Включите электрокардиограф, нажав на кнопку включения питания. При этом должны светиться: индикатор включения успокоения, один из индикаторов чувствительности (20, 10, 5 мм/мВ) и индикатор переключателя отведений, указывающий включение калибровочного отведения «1mV».
5. Установите чувствительность электрокардиографа в положение 10 мм/мВ, нажимая кнопку переключателя чувствительности.
6. Установите тепловое перо на середину поля записи регулятором смещения пера.
7. Включите протяжку ленты, кратковременно нажав на кнопку включения скорости «25».
8. Запишите 2 – 3 калибровочных сигнала, кратковременно нажав на кнопку калибровки «1mV». (При этом индикатор рода работ должен находиться в позиции «1mV»).
9. Выключите протяжку ленты, кратковременно нажав на кнопку скорости «25».
10. Установите переключатель отведений в положение «1», кратковременно нажав на кнопку переключателя отведений.
11. Включите протяжку ленты с необходимой скоростью (25 или 50 мм/с) и запишите требуемое число циклов электрокардиограмм (по два для каждого студента).
12. Обозначьте зубцы электрокардиограммы сообразно рисунку 3.
13. Зная результат калибровки и скорость движения ленты, рассчитайте длительность сердечного цикла (R – R), интервала Q – T и амплитуды зубцов P,Q,R,S,T (в мВ).
РЕЗУЛЬТАТЫ
 Полученный фрагмент ЭКГ:
Полученный фрагмент ЭКГ:
Выводы:
| Дата (дд.мм.гг) | Преподаватель | Отметка о зачете лабораторной работы | Подпись преподавателя |
Контрольные вопросы:
1. Что называется электрокардиографией?
2. В чем суть теории Эйнтховена?
3. Как, пользуясь электрокардиограммой, определить величину биопотенциалов сердца в различные моменты сердечного цикла и частоту пульса?
|
|
|
4. Перечислите возможные помехи, искажающие ЭКГ.
ЗАНЯТИЕ № 22
| Тема раздела: | Электрические и магнитные явления в организме, электрические воздействия и методы исследования |
| Тема занятия: | Цепи переменного электрического тока |
| Цель занятия: | Изучить зависимость индуктивного и емкостного сопротивлений от частоты переменного электрического тока. |
Теоретические вопросы:
1. Переменный электрический ток и его физические характеристики.
2. Цепь переменного электрического тока с активным сопротивлением.
3. Цепь переменного электрического тока с индуктивным сопротивлением.
4. Цепь переменного электрического тока с емкостным сопротивлением.
5. Полное сопротивление цепи переменного электрического тока. Импеданс.
Литература
- Антонов В.Ф. и др. Биофизика. –М.: Владос, -2000.
- Ремизов А. Н. и др. Медицинская и биологическая физика. –М.: Дрофа, -2003.
- Ремизов А. Н. и др. Медицинская и биологическая физика. –М.: Высшая школа, -1996.
- Губанов Н.И., Утепбергенов А.А. - Медицинская биофизика, -М.: Медицина, 1978.
- Владимиров Ю. А. и др. Биофизика. –М.: Медицина, 1983.
- Конспект лекций.
Краткое содержание теории
Переменным током называют ток, периодически изменяющийся по величине и по направлению.
Переменный ток можно рассматривать как вынужденные электромагнитные (электрические колебания).
Наиболее распространенным является синусоидальный переменный ток, мгновенные значения которого изменяются во времени по закону синуса (косинуса) или по закону простого (гармонического) колебания.
ф = B S0,
где ф - магнитный поток; В - магнитная индукция.
 (закон Фарадея или закон электромагнитной индукции);
(закон Фарадея или закон электромагнитной индукции);

где  .
.
Соответственно, мгновенные значения напряжения " U " или тока " I " во внешней цепи генератора:
U = Um sinwt или I = Im sinwt,
где Um и Im - максимальные (амплитудные) значения, соответственно, напряжения и тока, w = 2pn - круговая частота переменного напряжения или тока.
Кроме мгновенных и амплитудных значений, для характеристики переменного тока пользуются эффективными или действующими (средними квадратичными за период) значениями напряжения и тока, которые обычно и указываются на шкале измерительных приборов. Для синусоидального переменного тока:
|
|
|


Назовем действующей или эффективной силой переменного тока Iэф такой постоянный ток, который выделяет в цепи с сопротивлением R количество теплоты, одинаковое с переменным током:
Pср = P,  ;
;
средняя мощность Pср = UэфIэф cosj.
Переменный ток - это также упорядоченное (направленное) движение носителей заряда, однако оно имеет колебательный характер. Электрическое поле изменяет свое направление на противоположное каждую половину периода.
Соответственно изменяется и направление перемещения зарядов в проводниках. Величина перемещения весьма мала и зависит от частоты переменного тока. Например, при средней скорости дрейфа электронов в металлическом проводнике порядка 0,1 см/сек и при частоте тока 50 Гц смещение электронов имеет порядок 0,001 см. Для ионов в растворе электролита эта величина еще меньше.
При достаточно высокой частоте это смещение становится такого же порядка, как и смещение зарядов в тепловом движении. Однако колебания зарядов, образующих ток, от последнего отличаются упорядоченным (направленным) характером.
Переменный ток частотой 4:-5 кГц применяется, подобно импульсным токам, для цепей электростимуляции, а частотой 20-30кГц (при малых силах тока) - при измерении, например, полного сопротивления тканей организма. Переменный ток 200 кГц и выше даже при значительных силах тока раздражающего действия на ткани организма не оказывает, но тепловой эффект тока при этом сохраняется, поэтому высокочастотные токи применяются для тепловых лечебных процедур - прогревания глубоко лежащих тканей организма.
Колебательное движение зарядов вносит ряд отличий в явления, происходящие в цепях переменного тока, по сравнению с постоянным. Например, конденсатор является проводником в цепи переменного тока; в цепи, содержащей индуктивность, постоянно действует э.д.с. самоиндукции, которая имеет также переменный характер; в цепи с раствором электролита не происходит электрической поляризации и потому сопротивление такой цепи (а следовательно и тканей организма) при прочих равных условиях значительно меньше, чем при постоянном токе, и т.д.
|
|
|
Цепь переменного тока, содержащая омическое сопротивление R, не представляет особенностей. В ней выполняется закон Ома, который может быть применен как к мгновенным, так и эффективным значениям напряжения и тока:  .
.



Сопротивление R в цепи переменного тока называется активным, так как при прохождении тока в нем происходит необратимая потеря энергии, которая переходит в теплоту.
Колебания напряжения и тока в цепи с чисто активным сопротивлением находятся в фазе.
Рассмотрим явления, происходящие в цепи переменного тока с индуктивностью. Подключим к переменному напряжению U = Um sinwt катушку с индуктивностью " L ", активным сопротивлением которой за малостью можно пренебречь.



В цепи образуется переменный ток и в катушке возникает э.д.с. самоиндукции, равная 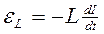 . Сила тока " I " в цепи определяется из условия:
. Сила тока " I " в цепи определяется из условия:  ,(так как сопротивлением " R " пренебрегаем) или
,(так как сопротивлением " R " пренебрегаем) или  .
.
Преобразуем 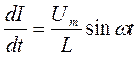 или
или 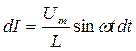 .
.
Интегрируем это уравнение
 , где
, где  .
.
Постоянная интегрирования принимается С = 0, так как не имеет постоянной составляющей. Уравнение показывает, что ток в цепи, подобно напряжению, имеет синусоидальный характер, но по фазе запаздывает на угол  .
.
Сопоставляя максимальное значение тока  с формулой закона Ома, видим, что в цепи с индуктивностью значение сопротивления имеет величина " wL ", которая обозначается XL..
с формулой закона Ома, видим, что в цепи с индуктивностью значение сопротивления имеет величина " wL ", которая обозначается XL..
Величина XL = wL = 2pnL называется индуктивным сопротивлением цепи и измеряется в Омах, при подстановке L - в Генри и n - в Герцах.
Физический смысл индуктивного сопротивления состоит в том, что оно учитывает влияние на силу тока в цепи э.д.с. самоиндукции, противодействующей приложенному напряжению, и поэтому зависит от тех же величин, что и э.д.с. самоиндукции: индуктивности " L " и частоты w = 2pn, обусловливающей скорость изменения мгновенных значений тока.
Э.д.с. самоиндукции, противодействующая изменению тока в цепи, вызывает запаздывание колебаний тока, по отношению к колебаниям напряжения. При чисто индуктивной цепи запаздывание происходит на угол, равный  .
.
Графики напряжения и тока в цепи с индуктивностью показаны на рисунке. На векторной диаграмме показано фазовое соотношение векторов амплитуд тока IL и напряжения UL: ток отстает на угол 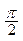 (углы отсчитываются по направлению против часовой стрелки).
(углы отсчитываются по направлению против часовой стрелки).
В цепи, содержащей индуктивное и активное сопротивление, угол запаздывания тока по фазе будет меньше и в зависимости от соотношения между ними может иметь значения в пределах от 0 до  .
.
В чисто индуктивном сопротивлении потерь энергии не происходит, в связи с чем оно называется реактивным.
|
|
|
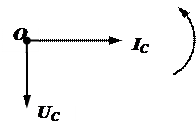
Определим характер переменного тока " I " в цепи с конденсатором, к которой приложено переменное напряжение U = Um sinwt.


Мгновенные значения заряда " q" на пластинах конденсатора
q = cU = cUm sin wt.
Дифференцируем

где Im = wcUm. Это уравнение показывает, что ток в цепи, подобно напряжению, имеет синусоидальный характер (смотри рисунок), причем упреждает напряжение по фазе на угол  .
.
Сопоставляя максимальное значение тока Im = wcUm с формулой закона Ома, видим, что в цепи с емкостью значение сопротивления имеет величина  , которая обозначается Xc.
, которая обозначается Xc.
Величина  называется емкостным сопротивлением цепи и измеряется в Омах, если с - в Фарадах и n - в Герцах.
называется емкостным сопротивлением цепи и измеряется в Омах, если с - в Фарадах и n - в Герцах.
Физический смысл емкостного сопротивления можно объяснить так: ток " I " в цепи конденсатора пропорционален заряду " q " и частоте " n " смены процессов заряда и разряда конденсатора. Заряд " q " при данном приложенном напряжении " U " пропорционален емкости " с " конденсатора, а w = 2pn. Поэтому ток " I " в цепи пропорционален произведению " wc ", которое, следовательно, имеет значение проводимости цепи. Величина, ей обратная, то есть 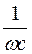 , имеет значение сопротивления цепи.
, имеет значение сопротивления цепи.
В цепи, содержащей емкость и активное сопротивление, угол сдвига фазы тока будет меньше и в зависимости от соотношения между ними может иметь значения от 0 до 900.
В чисто емкостном сопротивлении потерь энергии не происходит, в связи с чем оно называется реактивным.
Имеется цепь из включенных последовательно сопротивлений: активного " R", индуктивного " XL " и емкостного " Xc ", к которой приложено переменное напряжение " U ". В цепи образуется общий ток " I ", а приложенное напряжение " U " распределяется между участками цепи:
UR = IR; UL = IXL и Uc = Ixc.



Вследствие наличия разности фаз между напряжениями UL и Uc и током I (UR находится в фазе с током) эти напряжения должны складываться между собой векторно (геометрически), образуя в сумме приложенное напряжение " U ".
Напряжения UL и Uc имеют разность фаз с током I, равную  , но противоположную по знаку, то есть они находятся между собой в противофазе и, следовательно, могут складываться алгебраически:
, но противоположную по знаку, то есть они находятся между собой в противофазе и, следовательно, могут складываться алгебраически:
Ux = UL - Uc (обычно UL > Uc).
Напряжение UR находится в фазе с током I и, следовательно, имеет разность фаз  с напряжением Ux = UL - Uc. Тогда напряжение U как гипотеза прямоугольного треугольника, катетами которого являются UR и Ux, и вычисляются по формуле:
с напряжением Ux = UL - Uc. Тогда напряжение U как гипотеза прямоугольного треугольника, катетами которого являются UR и Ux, и вычисляются по формуле:
 ,
,
где 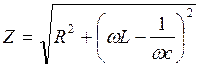 ,
,
называется полным сопротивлением (или импедансом) цепи.
Соотношение  называется обобщенным законом Ома для цепи переменного тока.
называется обобщенным законом Ома для цепи переменного тока.
Разность фаз между приложенным напряжением U и током I определяется углом y между векторами U и UR.
Аналогично можно построить и треугольник сопротивлений. В нём
 .
.
Из треугольника имеем  .
.
Путем аналогичных рассуждений для цепи из параллельно включенных активного, индуктивного и емкостного сопротивлений можно получить следующее соотношение:

Резонанс в цепи переменного тока
Из формулы для полного сопротивления " Z " контура, в котором последовательно включены R,L, и C, следует, что чем ближе по величине XL и Xc ( то есть wL и 1¤wc), тем меньше полное сопротивление " Z " и, следовательно, тем больше ток в цепи при том же приложенном напряжении " U ".
При XL = Xc или wL = 1¤wc полное сопротивление Z = R и ток достигает наибольшего значения, обусловленного только активным сопротивлением цепи:
 .
.
Это явление называют электрическим резонансом. Условие резонанса может быть обеспечено путем подбора соответствующих L и C при заданной частоте w или, наоборот, при заданных L и C путем соответствующей частоты " w ", которая называется резонансной (или собственной частотой электрической цепи. Из условия  c следует
c следует  и
и  , соответственно,
, соответственно, 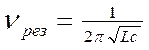 .
.
 На рисунке приведен график резонансной кривой, показывающей характер изменения тока при изменении частоты питающего напряжения вблизи от резонансной. Чем меньше активное сопротивление R цепи, тем острее резонанс (кривая А при малом R, кривая Б при значительном R).
На рисунке приведен график резонансной кривой, показывающей характер изменения тока при изменении частоты питающего напряжения вблизи от резонансной. Чем меньше активное сопротивление R цепи, тем острее резонанс (кривая А при малом R, кривая Б при значительном R).
Резонанс в последовательной цепи называют резонансом напряжений, так как при этом происходит взаимная компенсация напряжений UL и Uc, каждое из которых порознь может значительно превышать по величине приложенное напряжение " U " к цепи.
Резонанс может иметь место также в цепи из параллельно включенных активного, индуктивного и емкостного сопротивлений, к которой приложено переменное напряжение " U ". Это явление называется резонансом токов и представляет особый интерес, так как имеет место в генераторе электрических колебаний.
Самостоятельно решить задачи:
№№ 4.70, 4.71, 4.72, 4.73.
(А.Н.Ремизов и др. Сборник задач по медицинской и биологической физике. –М.: Высшая школа, -1987)
Практически выполнить:
| Лабораторная работа: | Определение зависимости индуктивного и емкостного сопротивлений от частоты |
| Цель работы: | Изучить зависимость емкостного и индуктивного сопротивлений от частоты переменного тока, построить графики |
| Оборудование и принадлежности: | усилитель постоянного тока с включенными на выходе тремя фильтрами, вольтметр переменного тока В3-38, вольтметр В7-40/3, генератор низкочастотный Г3-131 |
Описание установки
На столе собрана электрическая схема, состоящая из генератора переменного тока, с выхода которого электрический сигнал подается через миллиамперметр посредством ключа или на индуктивность, или на емкость. Выходное напряжение генератора контролируется по вольтметру переменного тока В3-38. Сила тока через индуктивность или емкость определяется с помощью миллиамперметра.
Содержание работы
| 1. | Определение зависимости индуктивного сопротивления от частоты. | ||||||||||||||||||||||
| А. | Включить генератор низкочастотный Г3-131 и вольтметр переменного тока В3-38 (тумблер «Сеть») 1) установить частоту выходного сигнала генератора n=200 Гц, используя кнопку «Частота» «2 kHz», ручки «Частота» «Грубо», «Плавно», переключатель «Аттенюатор» в положении 0 дб; 2) установить ручкой “АМПЛ” генератора по шкале вольтметра (В3-38) необходимое выходное напряжение генератора 5 В. | ||||||||||||||||||||||
| Б. | Включить вольтметр В7/40 (тумблер «Сеть»). Переключатель «ПРЕДЕЛЫ» пределов измерения тока установить в положение «АВП» (нажать кнопку «АВП»), что означает автоматический выбор пределов шкалы. Перевести вольтметр в режим измерения силы переменного тока (см. кнопки «РОД РАБОТЫ»), для чего нажать кнопку «I~». Единица измерения отображается на светодиодном индикаторе справа от цифрового индикатора (для тока «мА»). | ||||||||||||||||||||||
| В. | Установить ключ на лабораторной панели в положение «L». | ||||||||||||||||||||||
| Г. | Вращением ручек «Частота» «Грубо», «Плавно» устанавливаем необходимые значения частот (200 ¸ 1100 Гц). | ||||||||||||||||||||||
| n (Гц) | |||||||||||||||||||||||
| IL (мА) | |||||||||||||||||||||||
| ZL (кОм) | |||||||||||||||||||||||
| XL(кОм) | |||||||||||||||||||||||
| Д. | Для каждого значения частоты снимаем показания силы тока IL (мА) с вольтметра В7/40. | ||||||||||||||||||||||
| Е. | Производим вычисления  , где U=5 В и так как , где U=5 В и так как  , где R = 1,3 кОм – омическое сопротивление катушки (указано на катушке), то , где R = 1,3 кОм – омическое сопротивление катушки (указано на катушке), то  . .
| ||||||||||||||||||||||
| Ж. | Для частоты n=400 Гц вычислить  , где XL- индуктивное сопротивление на этой частоте. , где XL- индуктивное сопротивление на этой частоте.
| ||||||||||||||||||||||
| З. | Данные занести в таблицу, построить график зависимости XL=f(n).
Графическая зависимость
индуктивного сопротивления от частоты.

| ||||||||||||||||||||||
| 2. | Определение зависимости емкостного сопротивления от частоты. | ||||||||||||||||||||||
| А. | Установить ключ на лабораторной панели в положение «С». | ||||||||||||||||||||||
| Б. | установить частоту выходного сигнала генератора n=2000 Гц, используя кнопку “ЧАСТОТА” «20 kHz», ручки «ЧАСТОТА», «Грубо», «Плавно», переключатель «АТТЕНЮАТОР» в положении 0 дб. Вращением ручек “ЧАСТОТА“ «Грубо», «Плавно» устанавливаем необходимые значения частот (2000 ¸ 10000 Гц через 1000 Гц). | ||||||||||||||||||||||
| В. | Производим вычисления  , где U=5 В. , где U=5 В.
| ||||||||||||||||||||||
| Г. | Для частоты n=2000 Гц вычислить 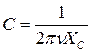 , где XС- емкостное сопротивление на этой частоте. , где XС- емкостное сопротивление на этой частоте.
| ||||||||||||||||||||||
| Д. | Данные занести в таблицу, построить график зависимости XС=f(n).
Графическая зависимость
емкостного сопротивления от частоты.

| ||||||||||||||||||||||
| n (Гц) | |||||||||||||||||||||||
| Iс (мА) | |||||||||||||||||||||||
| Е. | Нарисуйте в отчете по лабораторной работе электрическую схему измерения индуктивного и емкостного сопротивлений, представляя генератор, как источник переменного тока с подключенным к выходу вольтметром. | ||||||||||||||||||||||
| Ж. | Сделайте вывод о частотной зависимости индуктивного и емкостного сопротивлений. | ||||||||||||||||||||||
Электрическая схема измерения индуктивного и емкостного сопротивлений
Выводы:
| Дата (дд.мм.гг) | Преподаватель | Отметка о зачете лабораторной работы | Подпись преподавателя |
ЗАНЯТИЕ № 23
| Тема раздела: | Электрические и магнитные явления в организме, электрические воздействия и методы исследования |
| Тема занятия: | Электропроводность биологических тканей для постоянного и переменного тока. Физические основы реографии |
| Цель занятия: | Изучить особенности электропроводности биологических тканей для постоянного и переменного токам. Знать физические основы оценки жизнеспособности тканей и органов по частотной зависимости импеданса. |
Теоретические вопросы:
- Электропроводность электролитов.
- Первичное действие постоянного тока на ткани организма. Гальванизация. Лекарственный электрофорез.
- Электропроводность биотканей для переменного тока. Зависимость импеданса биологических объектов от частоты электрического тока.
- Реография как диагностический метод.
- Оценка жизнеспособности тканей путем измерения импеданса ткани при различных частотах переменного тока.
- Основы импедансной плетизмографии.
Литература
- Антонов В.Ф. и др. Биофизика. –М.: Владос, -2000.
- Ремизов А. Н. и др. Медицинская и биологическая физика. –М.: Дрофа, -2003.
- Ремизов А. Н. и др. Медицинская и биологическая физика. –М.: Высшая школа, -1996.
- Губанов Н.И., Утепбергенов А.А. - Медицинская биофизика, -М.: Медицина, 1978.
- Владимиров Ю. А. и др. Биофизика. –М.: Медицина, 1983.
- Конспект лекций.
Краткое содержание теории
Для описания как активных, так и реактивных свойств биологической ткани используется показатель импеданса Z – полного сопротивления ткани:
 ,
,
где R – активное сопротивление ткани, Х – реактивное сопротивление ткани, зависящее от ее емкостных свойств; 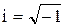 – мнимая единица. Использование мнимой единицы для записи величины импеданса позволяет не смешивать при расчетах омические и емкостные показатели.
– мнимая единица. Использование мнимой единицы для записи величины импеданса позволяет не смешивать при расчетах омические и емкостные показатели.
Кроме величин активной и реактивной составляющих импеданса, электрические свойства биологических тканей можно описать с помощью двух других показателей – модуля импеданса  и фазы импеданса j:
и фазы импеданса j: 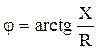 .
.
От показателей модуля и фазы импеданса всегда можно перейти к величинам активного и реактивного сопротивления тканей, и наоборот. Таким образом, две пары показателей, используемых для описания пассивных электрических свойств биологических тканей, эквивалентны.
При пропускании переменного электрического тока через биологические объекты в них возникают поляризационные процессы. Установлено, что при этом происходит изменение как активной, так и реактивной его составляющих импеданса. При исследовании электрических характеристик живых тканей в широком диапазоне частот переменного тока проявляется эффект дисперсии - модуль импеданса биологических объектов с увеличением частоты уменьшается до некоторой постоянной величины (рис. 23.1).
 Зависимость, подобная показанной на рис. 1, свойственна только живым тканям.
Зависимость, подобная показанной на рис. 1, свойственна только живым тканям.
Это подтверждает динамика кривых дисперсии, показывающих зависимость модуля импеданса ôZô растительной ткани от частоты в норме (рис. 23.2а), при нагревании ее в течение 2-х минут (рис. 23.2б) и при полном отмирании ткани (рис. 23.2в).
 Следует отметить ряд особенностей, характеризующих величину модуля импеданса живой ткани:
Следует отметить ряд особенностей, характеризующих величину модуля импеданса живой ткани:
1) значение ôZôдля живой ткани при измерениях в переменном токе ниже, чем при измерениях на постоянном токе;
2) значение ôZô не зависит от величины тока, если величина тока не превышает физиологическую норму;
3) ôZô на данной частоте постоянно, если не изменяется физиологическое состояние ткани;
4) ôZô изменяется при изменении физиологического состояния объекта.
Наличие в биологических системах емкостных сопротивлений подтверждается сдвигом фаз между силой тока и напряжением. Величина сдвига фаз определяется соотношением емкостного и омического сопротивлений. Для биологических систем характерна большая величина сдвига фаз. Это показывает, что доля емкостного сопротивления в биологических объектах велика. Например, величины сдвига фаз, полученных на биологических объектах при частоте 1000 Гц:
· для кожи человека 55°,
· для нерва лягушки 84°,
· для мышцы кролика 65°.
Для изучения закономерностей прохождения переменного тока через биологические ткани используют эквивалентные схемы, т.е. такие комбинации соединения омического сопротивления и емкости, которые в первом приближении могут моделировать электрические параметры клеток.
Рассмотрим примеры несложных эквивалентных схем.
1. Схема состоит из последовательно включенных омического сопротивления R и конденсатора С (рис. 23.3а).

Рис. 23.3. Схема с последовательно включенными омическим R и емкостным С сопротивлениями (а) и график изменения модуля импеданса ôZô от частоты n (б)
На рис. 23.3б видно, что при малых частотах значения модуля импеданса для данной схемы будет большим, т.к. емкостное сопротивление при этом резко увеличивается (ôZô® ¥ при n®0), что не согласуется с характеристикой модуля импеданса для живой ткани. Живые ткани имеют определенные значения ôZô при постоянном токе (рис. 23.1).
2. Схема состоит из параллельно включенных омического сопротивления и конденсатора (рис. 23.4а).

Рис. 4. Схема с параллельно включенными омическим R и емкостным С сопротивлениями (а) и график изменения модуля импеданса ôZô от частоты n (б)
Из рис. 4б видно, что при больших частотах значение модуля импеданса данной эквивалентной схемы стремится к нулю (ôZô® 0 при n® ¥). У живых объектов ôZô с увеличением частоты снижается только до определенных значений (рис.1).
Сравнивая графики, изображенные на рис. 3б и 4б, с зависимостью для живой ткани (рис. 23.1), легко заметить, что приведенные схемы не удовлетворяют всему диапазону частот исследования.
Приблизить свойства схемы к живой ткани позволяет электрическая схема, состоящая из нескольких элементов, соединенных последовательно и параллельно (рис. 5а). Зависимость модуля импеданса ôZô от частоты n для данной схемы представлена на рис.23.5б.

Рис. 23.5. Эквивалентная схема (а) и график зависимости модуля импеданса ôZ ôот частоты n (б)
Реография – метод исследования кровенаполнения органов и тканей или отдельных участков тела на основе регистрации их сопротивления переменному току высокой частоты.
Одна из причин изменения электрического сопротивления живых тканей – колебания их кровенаполнения. Использование высокочастотных токов необходимо для сведения к минимуму явлений поляризации в системе «электрод – кожа».
При применяемых в реографии частотах имеет место преимущественно ионная проводимость, так как проводниками служат жидкие среды организма, являющиеся слабыми электролитами. Ток при этом распространяется в основном по магистральным сосудам.
Изменения кровенаполнения и колебания электрического сопротивления тканей, расположенных между электродами, через которые пропускается ток высокой частоты, связаны формулой А.А. Кедрова:
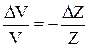 , (1)
, (1)
где  – относительное изменение объема ткани в исследуемом участке, практически равное изменению объема крови в этом участке;
– относительное изменение объема ткани в исследуемом участке, практически равное изменению объема крови в этом участке;  - относительное изменение полного сопротивленя этого участка. В течение сердечного цикла DZ изменяется в соответствии с изменением кровенаполнения исследуемого участка ткани: уменьшается при систоле и возрастает при диастоле. Графическая запись DZ во времени называется реограммой (рис.23.6).
- относительное изменение полного сопротивленя этого участка. В течение сердечного цикла DZ изменяется в соответствии с изменением кровенаполнения исследуемого участка ткани: уменьшается при систоле и возрастает при диастоле. Графическая запись DZ во времени называется реограммой (рис.23.6).

Рис. 23.6. Основные характеристики реограммы (h–амплитуда реограммы, h1 – амплитуда для расчета ударного объема крови, а – длительность восходящей части реограммы, Т–период реограммы, hк–высота калибровочного импульса)
В каждой реографической волне выделяют начало, вершину и конец, восходящую (анакротическую) и нисходящую (катокротическую) части. На нисходящей части могут наблюдаться 1 – 2 дополнительные волны.
Кривая в норме достаточно регулярна. Нарушения регулярности зависят от изменения ритма сердечных сокращений и дыхания. Регулярность может существенно нарушаться при патологии, например, при выраженной сосудистой дистонии.
Анализ реограмм производится по оценке её временных и амплитудных показателей.
Реограф – электронное устройство, предназначенное для преобразования колебаний импеданса живой ткани или его составляющих, обусловленных пульсовыми изменениями кровенаполнения в пропорциональный электрический сигнал.
Принцип работы реографа заключается в следующем: от генератора высокой частоты реографа с помощью электродов через исследуемый орган пропускается ток высокой частоты. При этом на исследуемом участке (органе) возникает падение напряжения. Изменения кровенаполнения в исследуемом органе приводят к изменениям его импеданса и пропорциональным изменениям амплитуды высокочастотного напряжения. После усиления с помощью детектора и фильтров выделяется низкочастотная составляющая, представляющая собой реографический сигнал (реограмму) – рис.23.7.

Используется переменный ток с частотами 30-300 кГц, величина тока составляет 1-5 мА.
Реоэнцефалография - метод исследования мозгового кровообращения, основанный на измерении и записи пульсовых колебаний полного электрического сопротивления (импеданса) головного мозга при пропускании через него тока высокой частоты, слабого по силе и напряжению.
ü Самостоятельно решить задачи:
№№ 4.19, 4.26, 4.27. (А.Н.Ремизов и др. Сборник задач по медицинской и биологической физике. –М.: Высшая школа, -1987)
Практически выполнить:
| Лабораторная работа: | Определение сопротивления живой ткани человека постоянному и переменному токам | ||||
| Цель работы: | · определить сопротивление кожи постоянному току; · определить сопротивление ткани организма переменному току; · найти угол сдвига фазы между током, протекающим через ткани, и приложенным к ней напряжением | ||||
| Оборудование и принадлежности: | А. Источник постоянного тока (аппарат гальванизации Поток-1 М), два неполяризующихся электрода, микроамперметр постоянного тока на 100 мкА, вольтметр постоянного тока на 6-12
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|

