 |
Распространение потенциала действия по миелиновым и безмиелиновым нервным волокнам
|
|
|
|
Впервые скорость распространения потенциала действия (возбуждения) по нервному волокну была измерена профессором физиологии Кенигсбергского университета Германом Гельмгольцем в 1850 году – спустя год после того как ученый И. Физо измерил скорость распространения света. Оказалось, что скорость распространения возбуждения составляет всего порядка 30 м/с. Значения скорости распространения ПД было примерно в 10 000 000 меньше скорости распространения электрического тока по металлическому проводнику и даже в 10 раз медленнее скорости распространения звука в воздухе.
Полученные результаты, с одной стороны, нанесли удар по сторонникам теории мгновенного распространения возбуждения, но одновременно и поставили исследователей перед необходимостью более детально изучить различия механизмов проведения электрического потенциала в проводниках и нервном волокне. Прежде всего, следовало дать ответ на вопросы: почему возбуждение способно распространяться по нервному волокну и от чего зависит скорость распространения нервного импульса.
Для того чтобы ответить на эти вопросы, рассмотрим электрические свойства нервного волокна. Оно представляет собой цилиндр, боковую поверхность которого образует мембрана, отделяющая внутренний раствор электролита от наружного. Это придает волокну свойства коаксиального кабеля, изоляцией которого служит клеточная мембрана. Но нервное волокно — очень плохой кабель. Сопротивление изоляции этого живого кабеля примерно в 105 раз меньше, чем у обычного кабеля, так как в первом случае ее толщина составляет 10 ~6 см, а во втором — около 10 см. Кроме того, внутренняя жила живого кабеля — это раствор электролита, удельное сопротивление которого в миллионы раз больше сопротивления металла. Поэтому невозбужденное нервное волокно плохо приспособлено для передачи электрических сигналов на большие расстояния. Было установлено, что уменьшение электрического потенциала на мембране нервного волокна по мере удаления от источника возбуждения убывает по экспоненциальному закону
|
|
|
 ,
,
где j0 – значение потенциала в точке возбуждения, jl –значение потенциала в точке, расположенной на расстоянии l от источника возбуждения, l - константа длины нервного волокна, равная расстоянию, на котором величина потенциала убывает в e (е =2,718281828…) раз.
Константа l зависит от удельного электрического сопротивления оболочки нервного волокна rm, удельного электрического сопротивления цитоплазмы ri, радиуса нервного волокна r:

 Чем больше l, тем больше скорость распространения нервного возбуждения. Как следует из приведенной выше формулы, l тем больше, чем больше радиус нервного волокна и чем больше удельное электрическое сопротивление мембраны нервного волокна.
Чем больше l, тем больше скорость распространения нервного возбуждения. Как следует из приведенной выше формулы, l тем больше, чем больше радиус нервного волокна и чем больше удельное электрическое сопротивление мембраны нервного волокна.
Для повышения скорости Природа использовала обе возможности. Для простейших организмов она создала нервные волокна большого диаметра – можно вспомнить гигантский аксон кальмара, диаметр которого достигает 0,5 мм.
Для более развитых животных такой путь был совершенно неприемлем – слишком много места в тканях занимали бы гигантские нервные волокна. Природа пошла по другому пути: создала «бронированные» нервные волокна, покрытые миелиновой изоляцией. Миелин представляет собой жироподобное вещество, которое повышает электроизоляцию нервных волокон (увеличивает удельное электрическое сопротивление клеточной мембраны). Причем миелин покрывает нервное волокно сегментами, длиной около 1 мм, а между сегментами имеются оголенные участки нервного волокна длиной около 1 мкм. Участки волокна, не покрытые миелином, получили название перехватов Ранвье. В области перехватов Ранвье мембрана имеет непосредственный контакт с внешним раствором. Наличие миелиновой оболочки позволяет увеличить скорость распространения возбуждения примерно в 25 раз по сравнению с немиелинизированным волокном, уменьшает энергозатраты организма, так как уменьшается общее количество ионов, пересекающих мембрану – ионы перемещаются только в области перехватов Ранвье.
|
|
|
Рассмотрим процесс распространения возбуждения по безмиелиновым нервным волокнам.
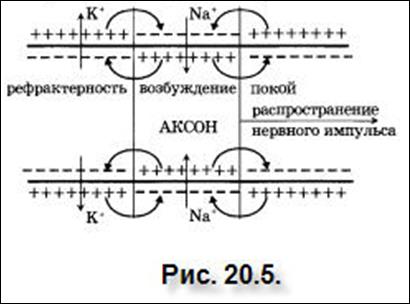 При возбуждении участка нервного волокна (см. рис. 20.5) происходит деполяризация данного участка. При деполяризации с наружной стороны мембран возникает отрицательный электрический потенциал, а с внутренней стороны – положительный потенциал. Между возбужденным и невозбужденным участками нервного волокна возникнут локальные электрические токи, так у возбужденного участка внутренняя поверхность имеет положительный заряд, а у невозбужденного участка – отрицательный электрический заряд и между ними возникает разность потенциалов. По поверхности нервного волокна локальный электрический ток течет от невозбужденного участка к возбужденному, внутри волокна электрический ток течет в обратном направлении – от возбужденного участка к невозбужденному.
При возбуждении участка нервного волокна (см. рис. 20.5) происходит деполяризация данного участка. При деполяризации с наружной стороны мембран возникает отрицательный электрический потенциал, а с внутренней стороны – положительный потенциал. Между возбужденным и невозбужденным участками нервного волокна возникнут локальные электрические токи, так у возбужденного участка внутренняя поверхность имеет положительный заряд, а у невозбужденного участка – отрицательный электрический заряд и между ними возникает разность потенциалов. По поверхности нервного волокна локальный электрический ток течет от невозбужденного участка к возбужденному, внутри волокна электрический ток течет в обратном направлении – от возбужденного участка к невозбужденному.
Эти локальные токи являются раздражителями для невозбужденных участков, непосредственно примыкающих к возбужденному участку. В них также возникает возбуждение (потенциал действия). В то же время локальные токи приводят к тому, что возбужденные участки приходят в состояние покоя – в них ПД сменяется ПП.
Возбужденные участки, в свою очередь, предают сигнал дальше, и процесс распространяется вдоль аксона. (Существует внешняя аналогия между распространением нервного импульса и распространением огня по бикфордову шнуру).
В миелинизированном волокне распространение импульса возбуждение происходит за счет локальных токов, которые вынуждены циркулировать между соседними перехватами Ранвье (см. рис. 20.6). Передача возбуждения происходит быстрее, чем в немиелинизированном волокне.

Калиевые и натриевые каналы открываются только в перехватах Ранвье, так как миелин является хорошим изолятором, таким образом импульс «перескакивает» с одного перехвата на другой – такое поведение называется сальтаторным. Миелинизация аксона позволяет достигать высокой скорости передачи импульса при очень малом диаметре волокна. Это дало позвоночным важное эволюционное преимущество, и во многом обусловило их дальнейшее развитие.
|
|
|
ü Практически выполнить:
| Лабораторная работа: | Компьютерное моделирование электрогенеза в клетках |
| Цель работы: | На основании математической модели Ходжкина-Хаксли, реализованной в среде пакета MathCad, исследовать особенности генерации потенциала действия. |
| Аппаратное и программное обеспечение: | ПК на основе МП Intel Celeron или AMD. Операционная система MS Windows XP. Пакет программ MathСad |
I. Теоретическая часть
С электрической точки зрения, клеточную мембрану можно представить как параллельно включенные конденсатор емкости и два источника натриевого и калиевого токов, имеющих Э.Д.С, направленных друг против друга, и внутренние сопротивления RK и RNa. Эти сопротивления являются переменными и зависят от калиевой GK и натриевой GNa проводимости (см. рис. 20.7).

Для полноты картины на рис. 20.7 изображено электрическое сопротивление R, которое учитывает проникновение через мембрану не только ионов калия и натрия, но и других ионов. Для мембраны аксона кальмара, которая практически не пропускает других ионов, сопротивлением R можно пренебречь. 
Ионы калия проходят в обе стороны через мембрану всегда. Когда потенциал на мембране V равен равновесному значению нернстовского потенциала VK, то на мембране сохраняется динамическое равновесие, суммарный поток ионов калия равен нулю, и калиевый ток равен нулю. При отклонении мембранного потенциала от равновесного значения возникает калиевый ток, величина которого определяется выражением:
 (1)
(1)
Аналогичную формулу можно записать и для натриевого тока:
 (2)
(2)
Суммарный ток, который протекает через конденсатор С (см. рис.1)
равен сумме натриевого, калиевого токов и тока I(t), подающегося на мембрану извне (например, тока возбуждения, если мы задались целью моделировать процесс генерации потенциала действия ПД):
|
|
|

 (3)
(3)
Силу тока, проходящего через конденсатор, можно определить, зная скорость изменения заряда на конденсаторе:
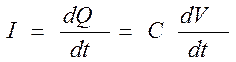 (4)
(4)
Объединяя уравнения (1) – (4), получим:
 (5)
(5)
На основании многочисленных экспериментов Ходжкин и Хаксли, с учетом уравнения (5), получили следующую систему уравнений, которая описывает все многообразие взаимосвязанных изменений во времени электрических характеристик мембраны:
 , (6)
, (6)
 , (7)
, (7)
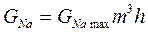 , (8)
, (8)
 , (9)
, (9)
 , (10)
, (10)
 , (11)
, (11)
 , (12)
, (12)
 , (13)
, (13)
 , (14)
, (14)
 , (15)
, (15)
 , (16)
, (16)
 . (17)
. (17)
Система уравнений (6) - (17) была создана Ходжкиным и Хаксли в 1952 г. и называется математической моделью Ходжкина–Хаксли (Х-Х). Для расчетов модели в те годы компьютеры недоступны (из-из их экзотичности – первая ЭВМ была создана в США в 1946 г. и использовалась почти исключительно для военных нужд) и Ходжкин с Хаксли вручную рассчитали, как меняется мембранный потенциал с течением времени, если на мембране создать возбуждение.
Сегодня при наличии персональных компьютеров (ПК) и современного программного обеспечения, реализация модели Х-Х (численные расчеты) не составит труда даже студенту-первокурснику.
Из программных сред, используемых для моделирования в области медицины и биологи на сегодняшний день, наиболее адекватным является пакет MathCad, в котором реализована идея «автоматизированного математического проектирования. Идея математического автоматизированного проектирования (МАП) позволяет специалисту-медику, который не имеет фундаментальных познаний в области численных методов и программирования, изучать и моделировать физиологические процессы, протекающие в живых организмах.
II. Практическая часть
q Исходное состояние – включен ПК, загружена операционная система Windows XP и имеется доступ к ресурсам локальной компьютерной сети (для получения доступа в сеть необходимо при загрузке Windows XP ввести имя пользователя Worker и парольWork).
1. С помощью созданного на Рабочем столе ярлыка загрузить пакет Mathcad.
2. Через команду “Файл” из меню команд загрузить файл c:\Мои документы\stud\ModelXX.mcd, содержащий модель ХХ, реализованную в среде пакета Mathcad.
3. В качестве исходных данных ввести следующие значения:
· VK:=-80
· VNa:=40
· GKO:=95
· GnaO:=180
· C:=0.9
· i:=0..50
· dt:=0.06
4. Проанализировать полученные графики, отражающие изменение потенциала на клеточной мембране, натриевой, калиевой проницаемости, проводимости мембраны с течением времени. Зарисовать в отчет по лабораторной работе графики (см. раздел «Отчет по лабораторной работе»), отражающие изменение во времени потенциала на клеточной мембране, натриевой, калиевой проницаемости, проводимости мембраны.
|
|
|
5. Закрыть окно с рабочим документом (файлом ModelXX.mcd), выбрав при закрытии (в обязательном порядке) «не сохранять изменения».
6. Закрыть Windows- приложение (пакет Mathcad).
7. Удалить ярлык, указывающий на Mathcad, очистив затем «Корзину».
8. Выключить ПК (если дана на то команда преподавателя) в соответствии с приведенной ниже инструкцией.
|
|
|


