Пузырьковая сортировка вставками.

Это модификация обменного варианта сортировки. В этом методе входное и выходное множества находятся в одной последовательности, причем выходное - в начальной ее части. В исходном состоянии можно считать, что первый элемент последовательности уже принадлежит упорядоченному выходному множеству, остальная часть последовательности - неупорядоченное входное. Первый элемент входного множества примыкает к концу выходного множества. На каждом шаге сортировки происходит перераспределение последовательности: выходное множество увеличивается на один элемент, а входное - уменьшается. Это происходит за счет того, что первый элемент входного множества теперь считается последним элементом выходного. Затем выполняется просмотр выходного множества от конца к началу с перестановкой соседних элементов, которые не соответствуют критерию упорядоченности. Просмотр прекращается, когда прекращаются перестановки. Это приводит к тому, что последний элемент выходного множества "выплывает" на свое место в множестве. Поскольку при этом перестановка приводит к сдвигу нового в выходном множестве элемента на одну позицию влево, нет смысла всякий раз производить полный обмен между соседними элементами - достаточно сдвигать старый элемент вправо, а новый элемент записать в выходное множество, когда его место будет установлено. Именно так и построен программный пример пузырьковой сортировки вставками - 3.12.

{===== Программный пример 3.12 =====} Procedure Sort (var a: Seq); Var i, j, k, t: integer; begin for i:=2 to N do begin { перебор входного массива } {*** вх.множество - [i..N], вых.множество - [1..i] } t:=a[i]; { запоминается значение нового эл-та } j:=i-1; {поиск места для эл-та в вых. множестве со сдвигом} { цикл закончится при достижении начала или, когда будет встречен эл-т, меньший нового } while (j >= 1) and (a[j] > t) do begin a[j+1]:=a[j]; { все эл-ты, большие нового сдвигаются } j:=j-1; { цикл от конца к началу выходного множества } end; a[j+1]:=t; { новый эл-т ставится на свое место } end; end;

Результаты трассировки программного примера 3.11 представлены в таблице 3.8.

Шаг	Содержимое массива a
Исходный	48:43 90 39_ 9 56 40 41 75 72
	43 48:90 39_ 9 56 40 41 75 72
	43 48 90:39_ 9 56 40 41 75 72
	39 43 48 90:_9 56 40 41 75 72
	_9 39 43 48 90:56 40 41 75 72
	_9 39 43 48 56 90:40 41 75 72
	_9 39 40 43 48 56 90:41 75 72
	_9 39 40 41 43 48 56 90:75 72
	_9 39 40 41 43 48 56 75 90:72
Результат	_9 39 40 41 43 48 56 72 75 90:

Таблица 3.8

Хотя обменные алгоритмы стратегии включения и позволяют сократить число сравнений при наличии некоторой исходной упорядоченности входного множества, значительное число пересылок существенно снижает эффективность этих алгоритмов. Поэтому алгоритмы включения целесообразно применять к связным структурам данных, когда операция перестановки элементов структуры требует не пересылки данных в памяти, а выполняется способом коррекции указателей (см. главу 5).

Еще одна группа включающих алгоритмов сортировки использует структуру дерева. Мы рекомендуем читателю повторно вернуться к рассмотрению этих алгоритмов после ознакомления с главой 6.

Сортировка упорядоченным двоичным деревом.

Алгоритм складывается из построения упорядоченного двоичного дерева и последующего его обхода. Если нет необходимости в построении всего линейного упорядоченного списка значений, то нет необходимости и в обходе дерева, в этом случае применяется поиск в упорядоченном двоичном дереве. Алгоритмы работы с упорядоченными двоичными деревьями подробно рассмотрены в главе 6. Отметим, что порядок алгоритма - O(N*log2(N)), но в конкретных случаях все зависит от упорядоченности исходной последовательности, который влияет на степень сбалансированности дерева и в конечном счете - на эффективность поиска.

Турнирная сортировка.

Этот метод сортировки получил свое название из-за сходства с кубковой системой проведения спортивных соревнований: участники соревнований разбиваются на пары, в которых разыгрывается первый тур; из победителей первого тура составляются пары для розыгрыша второго тура и т.д. Алгоритм сортировки состоит из двух этапов. На первом этапе строится дерево: аналогичное схеме розыгрыша кубка.

Например, для последовательности чисел a:

16 21 8 14 26 94 30 1

такое дерево будет иметь вид пирамиды, показанной на рис.3.13.

Рис.3.13. Пирамида турнирной сортировки

В примере 3.12 приведена программная иллюстрация алгоритма турнирной сортировки. Она нуждается в некоторых пояснениях. Построение пирамиды выполняется функцией Create_Heap. Пирамида строится от основания к вершине. Элементы, составляющие каждый уровень, связываются в линейный список, поэтому каждый узел дерева помимо обычных указателей на потомков - left и right - содержит и указатель на "брата" - next. При работе с каждым уровнем указатель содержит начальный адрес списка элементов в данном уровне. В первой фазе строится линейный список для нижнего уровня пирамиды, в элементы которого заносятся ключи из исходной последовательности. Следующий цикл while в каждой своей итерации надстраивает следующий уровень пирамиды. Условием завершения этого цикла является получение списка, состоящего из единственного элемента, то есть, вершины пирамиды. Построение очередного уровня состоит в попарном переборе элементов списка, составляющего предыдущий (нижний) уровень. В новый уровень переносится наименьшее значение ключа из каждой пары.

Следующий этап состоит в выборке значений из пирамиды и формирования из них упорядоченной последовательности (процедура Heap_Sort и функция Competit). В каждой итерации цикла процедуры Heap_Sort выбирается значение из вершины пирамиды - это наименьшее из имеющихся в пирамиде значений ключа. Узел-вершина при этом освобождается, освобождаются также и все узлы, занимаемые выбранным значением на более низких уровнях пирамиды. За освободившиеся узлы устраивается (снизу вверх) состязание между их потомками. Так, для пирамиды, исходное состояние которой было показано на рис 3., при выборке первых трех ключей (1, 8, 14) пирамида будет последовательно принимать вид, показанный на рис.3.14 (символом x помечены пустые места в пирамиде).

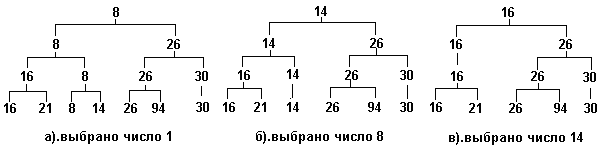
Рис.3.14. Пирамида после последовательных выборок

Процедура Heap_Sort получает входной параметр ph - указатель на вершину пирамиды. и формирует выходной параметр a - упорядоченный массив чисел. Вся процедура Heap_Sort состоит из цикла, в каждой итерации которого значение из вершины переносится в массив a, а затем вызывается функция Competit, которая обеспечивает реорганизацию пирамиды в связи с удалением значения из вершины.

Функция Competet рекурсивная, ее параметром является указатель на вершину того поддерева, которое подлежит реорганизации. В первой фазе функции устанавливается, есть ли у узла, составляющего вершину заданного поддерева, потомок, значение данных в котором совпадает со значением данных в вершине. Если такой потомок есть, то функция Competit вызывает сама себя для реорганизации того поддерева, вершиной которого является обнаруженный потомок. После реорганизации адрес потомка в узле заменяется тем адресом, который вернул рекурсивный вызов Competit. Если после реорганизации оказывается, что у узла нет потомков (или он не имел потомков с самого начала), то узел уничтожается и функция возвращает пустой указатель. Если же у узла еще остаются потомки, то в поле данных узла заносится значение данных из того потомка, в котором это значение наименьшее, и функция возвращает прежний адрес узла.

{===== Программный пример 3.12 =====} { Турнирная сортировка } type nptr = ^node; { указатель на узел } node = record { узел дерева } key: integer; { данные } left, right: nptr; { указатели на потомков } next: nptr; { указатель на "брата" } end; { Создание дерева - функция возвращает указатель на вершину созданного дерева } Function Heap_Create(a: Seq): nptr; var i: integer; ph2: nptr; { адрес начала списка уровня } p1: nptr; { адрес нового элемента } p2: nptr; { адрес предыдущего элемента } pp1, pp2: nptr; { адреса соревнующейся пары } begin { Фаза 1 - построение самого нижнего уровня пирамиды } ph2:=nil; for i:=1 to n do begin New(p1); { выделение памяти для нового эл-та } p1^.key:=a[i]; { запись данных из массива } p1^.left:=nil; p1^.right:=nil; { потомков нет } { связывание в линейный список по уровню } if ph2=nil then ph2:=p1 else p2^.next:=p1; p2:=p1; end; { for } p1^.next:=nil; { Фаза 2 - построение других уровней } while ph2^.next<>nil do begin { цикл до вершины пирамиды } pp1:=ph2; ph2:=nil; { начало нового уровня } while pp1<>nil do begin { цикл по очередному уровню } pp2:=pp1^.next; New(p1); { адреса потомков из предыдущего уровня } p1^.left:=pp1; p1^.right:=pp2; p1^.next:=nil; { связывание в линейный список по уровню } if ph2=nil then ph2:=p1 else p2^.next:=p1; p2:=p1; { состязание данных за выход на уровень } if (pp2=nil)or(pp2^.key > pp1^.key) then p1^.key:=pp1^.key else p1^.key:=pp2^.key; { переход к следующей паре } if pp2<>nil then pp1:=pp2^.next else pp1:=nil; end; { while pp1<>nil } end; { while ph2^.next<>nil } Heap_Create:=ph2; end; { Реорганизация поддерева - функция возвращает указатель на вершину реорганизованного дерева } Function Competit(ph: nptr): nptr; begin { определение наличия потомков, выбор потомка для реорганизации, реорганизация его } if (ph^.left<>nil)and(ph^.left^.key=ph^.key) then ph^.left:=Competit(ph^.left) else if (ph^.right<>nil) then ph^.right:=Competit(ph^.right); if (ph^.left=nil)and(ph^.right=nil) then begin { освобождение пустого узла } Dispose(ph); ph:=nil; end; else { состязание данных потомков } if (ph^.left=nil) or ((ph^.right<>nil)and(ph^.left^.key > ph^.right^.key)) then ph^.key:=ph^.right^.key else ph^.key:=ph^.left^.key; Competit:=ph; end; { Сортировка } Procedure Heap_Sort(var a: Seq); var ph: nptr; { адрес вершины дерева } i: integer; begin ph:=Heap_Create(a); { создание дерева } { выборка из дерева } for i:=1 to N do begin { перенос данных из вершины в массив } a[i]:=ph^.key; { реорганизация дерева } ph:=Competit(ph); end; end;

Построение дерева требует N-1 сравнений, выборка - N*log2(N) сравнений. Порядок алгоритма, таким образом, O(N*log2(N)). Сложность операций над связными структурами данных, однако, значительно выше, чем над статическими структурами. Кроме того, алгоритм неэкономичен в отношении памяти: дублирование данных на разных уровнях пирамиды приводит к тому, что рабочая область памяти содержит примерно 2*N узлов.

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: