Общие методические указания к решению задач

Решение задачи №1 требует знаний основных законов цепей постоянного тока; закона Ома, законов Кирхгофа, а также методики расчета эквивалентного сопротивления, вычисления мощности и работы электрического тока, составления баланса мощностей/ Рассмотрим несколько примеров:

Пример 1. Для схемы, приведенной на рисунке 1, а, определить эквивалентное сопротивление цепи R _ABи токи в каждом резисторе, а также расход электроэнергии цепью за 8 ч работы.

Решение. Задача относится к теме «Электрические цепи по­стоянного тока». Проводим поэтапное решение, предварительно обозна­чив стрелкой ток в каждом резисторе; индекс тока должен соответство­вать номеру резистора, по которому он проходит.

1.Определяем общее сопротивление разветвления R _CD, учитывая, что резисторы R₃ и R ₄соединены последовательно между собой, а с резистором R₅- параллельно:

R_CD= (R₃+ R₄) R₅ /(R₃+ R₄+ R₅ ) = (10+5) · 10/(10+ 5+ 10) = 6 Ом

схема принимает вид:(рисунок 1,б).

2. Определяем общее сопротивление цепи относительно вводов СЕ.

Резисторы R _CDи R₂ включены параллельно, поэтому

R_CE= R_CDR₂ / (R_CD+ R₂) = 6×3/(6 + 3) = 2 Ом

схема принимает вид:(рисунок 1, в).

3. Находим эквивалентное сопротивление всей цепи:

R_AB= R₁+ R_CE= 8 + 2 = 10 Ом (рисунок 1, г).

4. Определяем токи в резисторах цепи. Так как напряжение U_AB приложено ко всей цепи, а R_AB = 10 Ом, то согласно закону Ома I ₁= U_AB / R_AB= 150/ 10= 15 А.

Внимание! Нельзя последнюю формулу писать в виде I ₁= U_AB / R_1, так как U_AB приложено ко всей цепи, а не к участку R₁.

Для определения тока I ₂ находим напряжение на резисторе R₂, т. е. U_{CE .}

Очевидно, U_CE меньше U_AB на потерю напряжения в ре­зисторе R₁, т. е.

U_CE= U_AB- I₁R₁= 150 - 15 × 8 = 30 В.

 

Рисунок 1

 

Тогда I ₂= U_CE/ R₂= 30 / 3 = 10 A. Так как U_CE= U_CD, то можно определить токи I₃,₄и I₅,:

I₃,₄ = U_CD/ (R₃+ R₄) = =30/(10 + 5) = 2 A, I₅= U_CD/R₅= 30/10 = 3 A.

На основании первого закона Кирхгофа, записанного для узла С, проверим правильность определения токов:

I₁= I₂+ I₃,₄+ I₅, или 15 =10 + 2 + 3 = 15 А.

5. Расход энергии цепью за восемь часов работ:

W = Pt = U_ABI1t = 150 · 15 · 8 = 18000 Вт · ч = 18 кВт·ч.

Пусть в схеме примера 1 известны сопротивления всех резисторов, а вместо напряжения UAB задан один из токов, например I 2 = 2 А. Найти остальные токи и напряжение UAB. Зная I2, определяем U_CE = I₂R₂ = 2 · 3 = 6 В. Так как U_CE = U_CD, то

I ₃₄ = U_CD / (R ₃ + R ₄) = 6/ (10 + 5) = 0,4 A;

I ₅ = U_CD / R ₅ = 6/10 = 0,6 A.

На основании первого закона Кирхгофа I ₁ = I ₂ + I ₃₄ + I ₅ =2 + 0,4 + 0,6 = 3 A.

Тогда U_AB = U_CE + I ₁R₁ = 6 + 3 × 8 = 30 В.

При расплавлении предохранителя Пр5 резистор R₅ выключается и схема принимает вид, показанный на рисунке 1. д. Вычисляем эквивалентное сопротивление схемы:

R’_AB= R₁+ (R₃ + R₄). Так как напряжение U_AB остается неизменным, находим ток

I ₁ = U_AB / R’_AB = 150/10,5 = 14,28 A. Напряжение U _CE = U_AB – I ₁ R₁ = 150 - 14,28 · 8 =

= 35,75 В. Тогда токи I ₁ = U_CE / R₂= 35,75/3 = 11,9 A; I ₃₄ = U_CE / R₃₄ = 35,75/ (10 + 5) = 2,38 А.

Сумма этих токов равна току I= I₁ + I₃₄ = 11,9 + 2,38 = 14,28 A.

Ответ: выписать все полученные результаты.

 

Решение задачи 3 требует знания учебного материала об особенностях цепей переменного тока с активным, индуктивным и емкостным сопротивлениями, а также об особенностях соединения источников и потребителей в «звезду» и «треугольник».

 

Пример 2. Неразветвленная цепь переменного тока содержит катушку с активным сопротивлением R_к= 3 Ом и индуктивным Х_L = 12 Ом, активное сопротивление

R = 5 Ом и конденсатор с сопротивлением Хс = 6 Ом. К цепи приложено напряжение U = 100В (действующее значение).

Определить:

1) полное сопротивление цепи;

2) ток;

3) коэффициент мощности;

4) активную реактивную и полную мощности;

5) напряжение на каждом сопротивлении.

Начертить в масштабе векторную диаграмму цепи.

Решение 1. Определяем полное сопротивление цепи:

 

Z = √(Rк +R)² + (Х_L - Хс) ² = √(3 + 5)² + (12 – 6)² = 10 Ом

2. Определяем токи цепи: I = U/Z = 100/10 = 10А.

3. Находим коэффициент мощности цепи. Во избежание потери знака угла (косинус –функция четная) определяем sin φ: sin φ = (Х_L- Хс)/ Z = (12 – 6)/10 = 0,6; φ = 36˚50'. По таблице Брадиса определяем коэффициент мощности cos 36˚50' = 0,8.

 

 

а) б) Рисунок 2

4. Определяем активную реактивную и полную мощности цепи:

Р = U I cos φ = 100 * 10 * 0,8 = 800 Bт или Р = I² (Rк + R) = 10² (3+5) = 800 Bт;

Q = I² * (Х_L - Хс) =10² (12 - 6)= 600 вар или Q = U I sin φ = 1000*10*0,6 = 600 ВАр;

S = U I = 100*10 = 1000 B*A или S = I²Z = 10²*10= 1000 BA

 

или S = = √800² + 600² = 1000 BA

5. Определяем падения напряжения на сопротивлениях цепи: U_RК =10 * 3 = 30В;

U_L = Ix_L = 10 * 12 = 120В; U_R = IR = 10 * 5 =50В; Uc = Ix_c 10 * 6 =60В

Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом потоку: в 1см –2,0А и масштабом по напряжению в 1см –20В. Построение векторной диаграммы (рисунок 2, б) начинаем с вектора тока, который откладываем по горизонтали в масштабе 10А/2А/см = 5см.

Вдоль вектора тока откладываем векторы падений напряжения на активных сопротивлениях U_Rк и U_R: 30 В/20 В/см = 1,5см; 50 В/20 В/см = 2,5см

Из конца вектора U_R откладываем в сторону опережения вектора тока на 90° вектор падения напряжения U_L на индуктивном сопротивлении длиной 120В/20 В/см = 6см. Из конца вектора U_L откладываем в сторону отставания от вектора тока на 90° вектор падения напряжения на конденсаторе U_С длиной

60 В/20 В/см = 3 см. Геометрическая сумма векторов U_Rк, U_R, U_L, U_С равна полному напряжению, приложенному к цепи.

Ответ: выписываем все результаты вычислений.

Пример 3. Цепь переменного тока состоит из двух ветвей, соеди­ненных параллельно. Первая ветвь содержит катушку с активным R1 = 12 Ом и индуктивным xL= 16 Ом сопротивлениями; во вторую

 

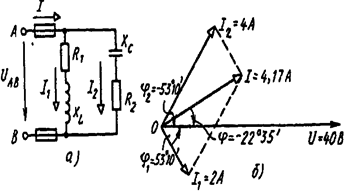
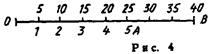
Рисунок 3

ветвь включен конденсатор с емкостным сопротивлением xC = 8 Ом и последовательно с ним активное сопротивление R 2 = 6 Ом. Активная мощность, потребляемая первой ветвью. P1 = 48 Вт (рисунок 3, а). Опре­делить: 1) токи в ветвях и в неразветвленной части цепи; 2) активные и реактивные мощности цепи; 3) напряжение, приложенное к цепи; 4) угол сдвига фаз между током в неразветвленной частя цепи и напряжением. Начертить в масштабе векторную диаграмму цепи.

Решение. 1. Активная мощность P₁теряется в активном cпротивлении R₁.

Поэтому P₁= I₁² R1₂.

Отсюда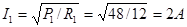

1. Определяем напряжение, приложенное к цепи:

U_AB=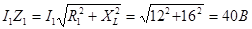

3. Определяем ток:

I₂ = U_AB / Z₂ = U_AB / R ₂ ² + Xc² = 40 / 12² + 16² = 4 А.

4. Находим активную и реактивную мощности, потребляемые цепью:

P = I₁ ² R₁ + I₂ ² R₂ = 2² · 12 + 4² · 6 = 154 Вт;

Q = I₁ ² Х_L _ I₂ ² Х_C = 2² · 16 _4² · 8 = _64 вар.

Знак «_» показывает, что преобладает реактивная мощность емкостного характера.

Полная мощность, потребляемая цепью,

S = R ² + Q ² = 154² + 64² = 166,8 В · А.

5. Определяем ток в неразветвленной части цепи:

I = S / UAB == 166,8 / 40 = 4,17 А.

6. Угол, сдвига фаз во всей цепи находим через sin φ во избежание потери знака угла:

sin φ = Q / S = _ 64/166,8 = _ 0,384; φ = _22°35'.

Знак «_» подчеркивает, что ток цепи опережает напряжение UAB.

Для построения векторной диаграммы определяем углы сдвига фаз в ветвях:

sin φ 1 = xL/Z1 = 16 / 12² + 16² = 0.8; φ 1 = 53° 10’;

sin φ 2 = xC/Z2 = _ 8 / 6² + 8² = _ 0.8; φ 2 = _53° 10’.

Задаемся масштабом по току: в 1 см — 1 А; по напряжению: в 1 см — 5 В. Построение начинаем с вектора напряжения (рисунок 3, б). Под углом φ 1 к нему в сторону отставания откладываем в масштабе вектор тока I_1: под углом φ 2 в сторону опережения — вектор тока I₂. Геометрическая сумма этих токов равна току в неразветвленной части цепи.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: