Расчет по прочности нормальных сечений на основе нелинейной деформационной модели

3.1.4.1 При расчете по прочности усилия и деформации в сечении, нормальном к продольной оси элемента, определяют на основе нелинейной деформационной модели, использующей уравнения равновесия внешних сил и внутренних усилий в сечении элемента, а также следующие положения:

распределение относительных деформаций бетона и арматуры по высоте сечения элемента от внешней нагрузки принимают по линейному закону (гипотеза плоских сечений);

связь между осевыми напряжениями и относительными деформациями бетона и арматуры принимают в виде диаграмм состояния (деформирования) бетона и арматуры (пп. 2.1.2.10, 2.2.2.7);

сопротивление бетона растянутой зоны допускается не учитывать, принимая при ε_bi ≥ 0 напряжения σ_bi = 0.

3.1.4.2 Переход от эпюры напряжений в бетоне к обобщенным внутренним усилиям определяют с помощью процедуры численного интегрирования напряжений по нормальному сечению. Для этого нормальное сечение условно разделяют на малые участки: при косом изгибе - по высоте и ширине сечения; при изгибе в плоскости оси симметрии поперечного сечения элемента - только по высоте сечения. Напряжения в пределах малых участков принимают равномерно распределенными (усредненными).

3.1.4.3 При расчете элементов с использованием нелинейной деформационной модели принимают:

значения сжимающей продольной силы, а также сжимающих напряжений и деформаций укорочения бетона и арматуры со знаком «-»;

значения растягивающей продольной силы, а также растягивающих напряжений и деформаций удлинения бетона и арматуры со знаком «+».

Знаки координат центров тяжести арматурных стержней и выделенных участков бетона, а также точки приложения продольной силы принимают в соответствии с назначенной системой координат Х0Y. В общем случае начало координат этой системы (точка 0 на рисунке 6) располагают в произвольном месте в пределах поперечного сечения элемента.

Рисунок 6 – Расчетная схема нормального сечения железобетонного элемента

3.1.4.4 При расчете нормальных сечений по прочности (см. рисунок 6) в общем случае используют:

уравнения равновесия внешних сил и внутренних усилий в нормальном сечении элемента

; (49)

; (50)

; (51)

уравнения, определяющие распределение деформаций от действия внешней нагрузки по сечению элемента

; (52)

; (53)

зависимости, связывающие напряжения и относительные деформации бетона и арматуры:

бетона

σ_bi = E_b ν_bi ε_bi; (54)

ненапрягаемой арматуры

σ_sj = E_sj ν_sj ε_sj; (55)

напрягаемой арматуры

σ_sj = E_sj ν_sj (ε_sj + ε_spj). (56)

В уравнениях (49)-(56):

М_х, М_у - изгибающие моменты от внешней нагрузки относительно выбранных и располагаемых в пределах поперечного сечения элемента координатных осей (соответственно действующих в плоскостях X0Z и У0Z или параллельно им), определяемые по формулам:

M_x = M_xd + N e_x; (57)

M_y = M_yd + N e_y, (58)

где	Mxd, Myd	- изгибающие моменты в соответствующих плоскостях от внешней нагрузки, определяемые из статического расчета конструкции;
	N	- продольная сила от внешней нагрузки; для изгибаемых предварительно напряженных элементов N = 0;
	ех, ey	- расстояния от точки приложения силы N до соответствующих выбранных осей;
	Аbi, Zbxi, Zbyi, σbi	- площадь, координаты центра тяжести i -го участка бетона и напряжение на уровне его центра тяжести;
	Asj, Zsxj, Zsyj, σsj	- площадь, координаты центра тяжести j- гостержня арматуры и напряжение в нем;
	ε0	- относительная деформация волокна, расположенного на пересечении выбранных осей (в точке 0);
	εbi	- относительная деформация бетона от действия внешней нагрузки;
	εsj	- относительная деформация арматуры от действия внешней нагрузки;
	εspj	- относительная деформация предварительного напряжения арматуры с учетом относительных деформаций потерь предварительного напряжения, отвечающих рассматриваемой расчетной стадии;
		- кривизна продольной оси в рассматриваемом поперечном сечении элемента в плоскостях действия изгибающих моментов Мx и My;
	Eb	- начальный модуль упругости бетона;
	Esj	- модуль упругости j- го стержня арматуры;
	νbi	- коэффициент упругости бетона i -го участка;
	νsj	- коэффициент упругости j -го стержня арматуры

Коэффициенты v_bi и ν_sj принимают по соответствующим диаграммам состояния бетона и арматуры, указанным в пп. 2.1.2.10, 2.2.2.7.

Значения коэффициентов v_bl и ν_sj определяют как соотношение значений напряжений и деформаций для рассматриваемых точек соответствующих диаграмм состояния бетона и арматуры, принятых в расчете, деленное на модуль упругости бетона Е_b (при двухлинейной диаграмме состояния бетона - на приведенный модуль деформации Е_b,_red)и арматуры E_s. При этом используют зависимости «напряжение - деформация» (4) - (8), (13) и (16) на рассматриваемых участках диаграмм.

; (58)

. (59)

3.1.4.5 Расчет нормальных сечений железобетонных элементов по прочности производят из условий

; (60)

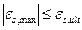, (61)

где ε_b,max - относительная деформация наиболее сжатого волокна бетона в нормальном сечении;

ε_s,max - относительная деформация наиболее растянутого стержня арматуры в нормальном сечении;

ε_b,ult - предельное значение относительной деформации бетона при сжатии, принимаемое согласно указаниям п. 3.1.4.6;

ε_s,ult - предельное значение относительной деформации удлинения арматуры, принимаемое согласно указаниям п. 3.1.4.6.

3.1.4.6 Предельные значения относительных деформаций бетона ε_b,ult (ε_bt,ult)принимают при двузначной эпюре деформаций (сжатие и растяжение) в поперечном сечении бетона элемента (изгиб, внецентренное сжатие или растяжение с большими эксцентриситетами), равными ε_b2 (ε_bt2).

При внецентренном сжатии или растяжении элементов и распределении в поперечном сечении бетона элемента деформаций только одного знака предельные значения относительных деформаций бетона ε_b,ult (ε_bt,ult)определяют в зависимости от соотношения деформаций бетона на противоположных гранях сечения элемента ε₁ и ε₂ (| ε₂ | ≥ | ε₁ |) по формулам:

; (62)

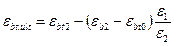, (63)

где ε_b0, ε_bt0, ε_b2, ε_bt2 - деформационные параметры расчетных диаграмм состояния бетона (пп. 2.1.2.5, 2.1.2.11, 2.1.2.13, 2.1.2.14).

Предельное значение относительной деформации арматуры ε_s,ult принимают равным:

0,025 - для арматуры с физическим пределом текучести;

0,015 - для арматуры с условным пределом текучести.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: