 |
Расчет ширины раскрытия трещин, нормальных к продольной оси элемента
|
|
|
|
4.2.3.1 Ширину раскрытия нормальных трещин определяют по формуле
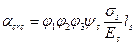, (88)
где σs - напряжение в продольной растянутой арматуре в нормальном сечении с трещиной от соответствующей внешней нагрузки, определяемое согласно п. 4.2.3.2;
l s - базовое (без учета влияния вида поверхности арматуры) расстояние между смежными нормальными трещинами;
ψs - коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами; допускается принимать коэффициент ψs = 1; если при этом условие (77) не удовлетворяется, значение ψs следует определять по формуле (96);
φ1 - коэффициент, учитывающий продолжительность действия нагрузки, принимаемый равным:
1,0 - при непродолжительном действии нагрузки;
1,4 - при продолжительном действии нагрузки;
φ2 - коэффициент, учитывающий профиль продольной арматуры, принимаемый равным:
0,5 - для арматуры периодического профиля и канатной;
0,8 - для гладкой арматуры (класса А240);
φ3 - коэффициент, учитывающий характер нагружения, принимаемый равным:
1,0 - для элементов изгибаемых и внецентренно сжатых;
1,2 - для растянутых элементов.
4.2.3.2 Значения напряжений σs в растянутой арматуре изгибаемых предварительно напряженных элементов от внешней нагрузки определяют по формуле
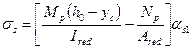, (89)
где Ired,Ared,yc - момент инерции, площадь приведенного поперечного сечения элемента и расстояние от наиболее сжатого волокна до центра тяжести приведенного сечения, определяемые с учетом площади сечения только сжатой зоны бетона, площадей сечения растянутой и сжатой арматуры согласно п. 4.3.3.5, принимая в соответствующих формулах значения коэффициента приведения арматуры к бетону αs2 = αs1;
|
|
|
Np - усилие предварительного обжатия (п. 4.1.4);
Мp - изгибающий момент от внешней нагрузки и усилия предварительного обжатия, определяемый по формуле
Mp = M ± Npe0p, (90)
где е0p - расстояние от точки приложения усилия предварительного обжатия Np до центра тяжести приведенного сечения.
Знак «-» в формуле (90) принимают, когда направления вращений моментов М и Npе0p не совпадают, и «+» - когда совпадают.
Значение коэффициента приведения арматуры к бетону αsl определяют по формуле
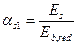, (91)
где Eb,red - приведенный модуль деформации сжатого бетона, учитывающий неупругие деформации сжатого бетона и определяемый по формуле
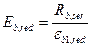. (92)
Относительную деформацию бетона εb1,red принимают равной 0,0015.
Допускается напряжение σs определять по формуле
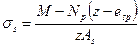, (93)
где z - расстояние от центра тяжести арматуры, расположенной в растянутой зоне сечения, до точки приложения равнодействующей усилий в сжатой зоне элемента;
еsp - расстояние от центра тяжести той же арматуры до точки приложения усилия Np.
Для элементов прямоугольного поперечного сечения при отсутствии (или без учета) сжатой арматуры значение z определяют по формуле
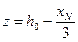, (94)
где xN - высота сжатой зоны, определяемая согласно п. 4.3.3.6 с учетом влияния усилия предварительного обжатия Np.
Для элементов прямоугольного, таврового (с полкой в сжатой зоне) и двутаврового поперечного сечения допускается значение z принимать равным 0,7 h0.
Напряжения σs, определяемые по формулам (89) и (93), не должны превышать (Rs,ser - σsp).
4.2.3.3 Значения базового расстояния между трещинами ls определяют по формуле
(95)
и принимают не менее 10 ds и 10 см и не более 40 ds и 40 см (для элементов с рабочей высотой поперечного сечения не более 1 м).
Здесь Аbt - площадь сечения растянутого бетона;
As - площадь сечения растянутой арматуры;
ds - номинальный диаметр арматуры.
Значения Аbt вычисляют согласно указаниям п. 4.2.2 из расчета по образованию трещин.
|
|
|
В любом случае значение Аbt принимают равным площади сечения при ее высоте в пределах не менее 2а и не более 0,5 h.
4.2.3.4 Значения коэффициента ψs определяют по формуле
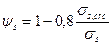, (96)
где σs,crc - напряжение в продольной растянутой арматуре в сечении с трещиной сразу после образования нормальных трещин, определяемое по указаниям п. 4.2.3.2, принимая в соответствующих формулах значения М = Мсrс;
σs - то же, при действии рассматриваемой нагрузки.
|
|
|
