 |
Внутренняя энергия идеального газа
|
|
|
|
МОЛЕКУЛЯРНАЯ ФИЗИКА
ГЛАВА 6. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
Уравнение состояния идеального газа
Согласно кинетической теории, газ представляет собой большое число молекул, находящихся в непрерывном хаотическом тепловом движении. Свойства газов (например, давление и температура) являются суммарным результатом действия молекул.
Рассмотрим модель идеального газа. Согласно этой модели молекулы газа — это маленькие шарики, суммарный объем которых всегда пренебрежимо мал по сравнению с объемом сосуда, в котором они находятся. Шарики не взаимодействуют между собой на расстоянии, а только непрерывно упруго сталкиваются друг с другом, двигаясь до соудорения прямолинейно и равномерно.
Получим уравнение состояния идеального газа — уравнение, связывающее параметры состояния газа — давление P, объем  и температуру
и температуру 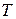 (в кельвинах).
(в кельвинах).
Опыт показывает, что при небольших давлениях легкие газы, такие как водород и гелий, с хорошей точностью подчиняются уравнению
 (15.1)
(15.1)
называемому уравнением Клапейрона. Следовательно, уравнение (15.1) можно считать уравнением состояния идеального газа. Постоянная 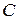 зависит от химического состава и количества газа.
зависит от химического состава и количества газа.
Обозначим через 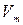 объема одного моля газа. Подставляя
объема одного моля газа. Подставляя  где
где  — число молей газа, в уравнение (15.1), имеем
— число молей газа, в уравнение (15.1), имеем

откуда

(15.2)
где постоянная  не зависит от количества газа. Кроме того, так как, согласно закону Авогадро, моли различных газов при одинаковых давлениях и температурах имеют одинаковый объем, постоянная
не зависит от количества газа. Кроме того, так как, согласно закону Авогадро, моли различных газов при одинаковых давлениях и температурах имеют одинаковый объем, постоянная

(15.3)
не зависит от химического состава газа, т. е. одинакова для всех газов. Поэтому ее принято называть универсальной газовой постоянной.
|
|
|
Найдем численное значение  . Известно, что при нормальных условиях
. Известно, что при нормальных условиях  1 атм =
1 атм =  Па,
Па, 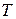 =273 К) объем моля газа
=273 К) объем моля газа  Согласно соотношению (15.3)
Согласно соотношению (15.3)

Подставляя  в уравнение (15.1), получаем уравнение состояния идеального газа
в уравнение (15.1), получаем уравнение состояния идеального газа

 (15.4)
(15.4)
называемое уравнением Клапейрона–Менделеева.
Пример 15.1. В баллоне вместимостью  находится аргон под давлением
находится аргон под давлением  и при температуре
и при температуре  Когда из баллона было взято некоторое количество газа, давление в баллоне понизилось до
Когда из баллона было взято некоторое количество газа, давление в баллоне понизилось до  а температура установилась
а температура установилась  Определить массу
Определить массу 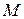 аргона, взятого из баллона.
аргона, взятого из баллона.
Дано:




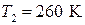
| Решение
 (Масса газа
(Масса газа  , где μ — масса моля
газа, , где μ — масса моля
газа,  — число молей газа). — число молей газа).
 . .


| ||

|

(см. Приложение 2).
Ответ: M = 33,2 г.
Пример 15.2. В баллонах объемом  и
и  содержится газ. Давление в первом баллоне
содержится газ. Давление в первом баллоне  во втором —
во втором —  Определить давление
Определить давление 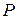 после соединение баллонов, если температура газа осталась прежней.
после соединение баллонов, если температура газа осталась прежней.
Дано:




| Решение
 




|

|

= 1,85·106 Па.
Ответ: P =1,85·МПа.
Внутренняя энергия идеального газа
Внутреннюю энергию  газа определяют как сумму кинетической энергии теплового движения молекул и потенциальной энергии межмолекулярного взаимодействия.
газа определяют как сумму кинетической энергии теплового движения молекул и потенциальной энергии межмолекулярного взаимодействия.
Получим выражение для внутренней энергии идеального газа. В идеальном газе пренебрегают силами межмолекулярного взаимодействия. Поэтому внутренняя энергия идеального газа равна кинетической энергии его молекул.
Расчет дает, что средняя кинетическая энергия молекул

(16.1)
где 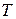 — температура газа,
— температура газа,  — постоянная Больцмана (
— постоянная Больцмана ( где NA — число Авогадро — число молекул в одном моле газа),
где NA — число Авогадро — число молекул в одном моле газа),  — число степеней свободы — число независимых координат, с помощью которых может быть задано положение молекул в пространстве. Для определения положения в пространстве одноатомной молекулы достаточно трех координат
— число степеней свободы — число независимых координат, с помощью которых может быть задано положение молекул в пространстве. Для определения положения в пространстве одноатомной молекулы достаточно трех координат  . Следовательно, для одноатомной молекулы
. Следовательно, для одноатомной молекулы  . Для определения положения в пространстве двухатомной молекулы достаточно трех координат
. Для определения положения в пространстве двухатомной молекулы достаточно трех координат  центра молекулы и двух значений углов φ и υ, фиксирующих направление оси молекулы. Следовательно, для двухатомной молекулы
центра молекулы и двух значений углов φ и υ, фиксирующих направление оси молекулы. Следовательно, для двухатомной молекулы  . Для определения положения трехатомной и более молекулы в пространстве достаточно трех координат
. Для определения положения трехатомной и более молекулы в пространстве достаточно трех координат  центра молекулы и трех значений углов φ, υ и ψ, фиксирующих направление оси молекулы. Следовательно, для трехатомной и многоатомной молекулы
центра молекулы и трех значений углов φ, υ и ψ, фиксирующих направление оси молекулы. Следовательно, для трехатомной и многоатомной молекулы  .
.
|
|
|
Пусть в сосуде находится N молекул идеального газа. Тогда с учетом выражения (16.1) внутренняя энергия идеального газа
 |
(16.2)
Учитывая, что

можем написать
 |
(16.3)
Отметим, что внутренняя энергия является функцией состояния. Это означает, например, что при переходе газа из состояния 1 (с температурой  ) в состояние 2 (с температурой
) в состояние 2 (с температурой  ) приращение внутренней энергии
) приращение внутренней энергии  , т. е. не зависит от способа перехода газа из состояния 1 в состояния 2, а определяется только разностью значений внутренней энергии газа в состояния 1 и 2.
, т. е. не зависит от способа перехода газа из состояния 1 в состояния 2, а определяется только разностью значений внутренней энергии газа в состояния 1 и 2.
Пример 16.1 Водород, находящийся при нормальных условиях в закрытом сосуде объемом V = 5 л охладили на  . Найти приращение внутренней энергии газа.
. Найти приращение внутренней энергии газа.
Дано:
 V = 5 л
V = 5 л

| Решение

 > >  . .

 . .
|

|
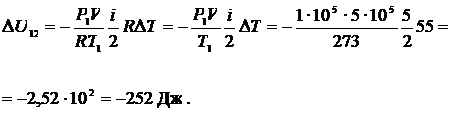
Ответ: 
Пример 16.2. Водород занимает объем  при давлении
при давлении  Его нагрели при постоянном объеме до давления
Его нагрели при постоянном объеме до давления  Определить приращение
Определить приращение  внутренней энергии газа.
внутренней энергии газа.
Дано:


 
| Решение

|
 
|
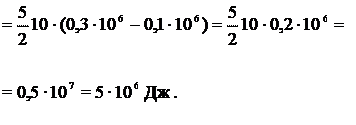
Ответ: 
Распределение Максвелла
Назовем состояние газа равновесным,если параметры состояния газа при отсутствии внешних воздействий остаются неизменными во времени.
Пусть газ находится в равновесном состоянии при температуре 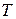 . Молекулы газа, непрерывно сталкиваясь между собой, меняют свои скорости как по направлению, так и по величине. Мы не можем сказать, с какой скоростью станет двигаться произвольно выбранная молекула в тот или иной момент времени. В то же самое время мы можем говорить о некотором стационарном (устойчивом) распределении молекул по скоростям: одни молекулы движутся быстро, другие медленно. Но на всякий интервал скоростей, например, от 10 до 20 м/с или от 20 до 30 м/с, будет приходиться в среднем (по времени) некоторое определенное число молекул. При отсутствии внешних воздействий установившееся при данной температуре распределение молекул по скоростям в дальнейшем не изменяется.
. Молекулы газа, непрерывно сталкиваясь между собой, меняют свои скорости как по направлению, так и по величине. Мы не можем сказать, с какой скоростью станет двигаться произвольно выбранная молекула в тот или иной момент времени. В то же самое время мы можем говорить о некотором стационарном (устойчивом) распределении молекул по скоростям: одни молекулы движутся быстро, другие медленно. Но на всякий интервал скоростей, например, от 10 до 20 м/с или от 20 до 30 м/с, будет приходиться в среднем (по времени) некоторое определенное число молекул. При отсутствии внешних воздействий установившееся при данной температуре распределение молекул по скоростям в дальнейшем не изменяется.
|
|
|
Определим вероятность того, что модуль скорости молекулы лежит между v и v + dv. Пусть 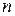 — общее число молекул в единице объема газа, а
— общее число молекул в единице объема газа, а  — число молекул в единице объема газа, скорости которых лежат между v и v + dv. Тогда искомая вероятность
— число молекул в единице объема газа, скорости которых лежат между v и v + dv. Тогда искомая вероятность

(17.1)
Введем величину
 |
(17.2)
— плотность вероятности, которая является функцией модуля скорости молекулы, в связи с чем ее называют функцией распределения вероятности молекул по скорости или просто функцией распределения молекул по скоростям.
Комбинируя формулы (17.1) и (17.2), получаем
 |
(17.3)
откуда
 (17.4)
(17.4)
Зная вид функции f (v), можно, интегрируя выражение (17.4), определить количество молекул в единице объема газа, скорости которых лежат в любом интервале скоростей.
Максвелл теоретически получил вид функции распределения молекул по скоростям:
 |
(17.5)
где  и
и 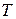 — масса молекулы и температура газа,
— масса молекулы и температура газа,  — постоянная Больцмана.
— постоянная Больцмана.

|
Изобразим график функции (17.5) (рис. 17.1).
Рис. 17.1
Из графика видно, что вероятность обнаружения в газе молекулы со скоростью, лежащей в интервале от v 1 до v 2 (см. формулу (17.2)).

равна заштрихованной площади под кривой f (v).
Вероятность обнаружения в газе молекул с любой скоростью от 0 до 
 |
(17.6)
т. е. площадь под всей кривой f (v) равна единице. Выражение (17.6) называют условием нормировки вероятности.
Скорость, соответствующая максимуму функции распределения f (v), будет наиболее вероятной v вер скоростью молекул. Найдем эту скорость.
Для  очевидно
очевидно

Продифференцируем выражение (17.5) по v и приравняем к нулю.

При v = 0 и v = ∞ функция f (v) минимальна. Следовательно, эти значения отбрасываем. Остается

откуда

Откуда получаем
 |
(17.7)
|
|
|
Используя функцию распределения (17. 5), можно найти среднюю  и среднюю квадратичную v кв скорости молекул:
и среднюю квадратичную v кв скорости молекул:
 |
(17.8)
 (17.9)
(17.9)
Барометрическая формула
До сих пор мы считали, что молекулы газа равномерно распределены по объему сосуда. Однако это не так. На молекулы газа действуют силы гравитационного притяжения Земли. Если бы не было теплового движения молекул атмосферного воздуха, то все они упали бы на землю. С другой стороны, если бы не было сил притяжения Земли, то атмосферный воздух рассеялся бы по всей Вселенной. Совместные действия гравитационного поля Земли и теплового движения молекул приводят к такому состоянию атмосферы, при котором число молекул 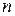 в единице объема и давление
в единице объема и давление 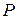 воздуха убывают с возрастанием высоты
воздуха убывают с возрастанием высоты 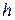 над земной поверхностью.
над земной поверхностью.
Найдем закон изменения давления газа с высотой в однородном гравитационном поле (ускорение свободного падения 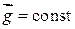 ). Будем считать, что газ находится в равновесном состоянии при температуре
). Будем считать, что газ находится в равновесном состоянии при температуре 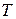 .
.
Согласно закону гидростатики, запишем выражение для давления газа на высотах 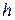 и
и  :
:


откуда

или
 |
(18.1)
где r — плотность газа.
Из уравнения Клапейрона–Менделеева

где 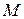 — масса газа в объемe V, μ — масса моля газа, следует
— масса газа в объемe V, μ — масса моля газа, следует

(18.2)
Подставляя выражение (18.2) в соотношение (18.1), получаем


или

(18.3)
Проинтегрируем выражение (18.3):

откуда
 |
(18.4)
где  — давление газа
— давление газа 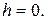
Представим зависимость (18.4) графически для двух газов с разными μ (рис. 18.1)

|
Рис.18.1
Из рис 18.1 видно, что давление газа убывает с высотой быстрее, чем тяжелее газ (чем больше μ). Следовательно, в верхних слоях атмосферы должны преобладать легкие газы.
Выражение (18.4) можно применять и для атмосферного воздуха, считая его газовой смесью с  Измеряя давление
Измеряя давление 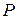 и
и  воздуха с помощью барометра, можно определить высоту
воздуха с помощью барометра, можно определить высоту

Поэтому выражение (18.4) называют барометрической формулой. Барометр, специально проградуированный для отсчета высоты над уровнем моря, называют альтиметром. Он широко применяется в авиации, в альпинизме и т. д.
Пример 18.1. Считая, что температура и молярная масса воздуха, а также ускорение свободного падения не зависят от высоты, найти разность высот, на которых плотности воздуха при температуре 0 °С отличаются в  раз.
раз.
Дано:

| Решение





|

|
 .
.

 .
.
 .
.
 .
.
 .
.


Ответ: 
Распределение Больцмана
Барометрическая формула (18.4) позволяет найти зависимость числа молекул 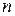 в единице объема газа от высоты
в единице объема газа от высоты 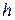 над земной поверхностью. По-прежнему будем считать, что газ находится в равновесном состоянии при температуре
над земной поверхностью. По-прежнему будем считать, что газ находится в равновесном состоянии при температуре 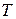 в однородном гравитационном поле (
в однородном гравитационном поле (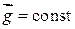 ).
).
|
|
|
Из уравнения Клапейрона–Менделеева следует
 |
(19.1)
где  — число молекул газа в единице объема.
— число молекул газа в единице объема.
Подставим выражение (19.1) в барометрическую формулу, имеем

(19.2)
где  — число молекул в единице объема газа при
— число молекул в единице объема газа при  .
.
Можем написать
 (19.3)
(19.3)
где  — масса молекулы,
— масса молекулы,  — постоянная Больцмана.
— постоянная Больцмана.
Подставляем формулу (19.3) в соотношение (19.2), получаем

(19.4)
или

 (19.5)
(19.5)
где  — потенциальная энергия молекулы газа в гравитационном поле Земли.
— потенциальная энергия молекулы газа в гравитационном поле Земли.
Следовательно, найденная зависимость (19.4) 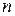 от
от 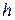 переходит в зависимость (19.5)
переходит в зависимость (19.5) 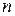 от
от  (рис. 19.1), согласно которой в объеме газа молекул будет больше там, где их потенциальная энергия меньше.
(рис. 19.1), согласно которой в объеме газа молекул будет больше там, где их потенциальная энергия меньше.

|
Рис. 19.1
Больцман доказал, что распределение (19.5) справедливо не только для молекул газа в потенциальном гравитационном поле Земли, но и для совокупности любых одинаковых хаотически движущихся частиц в любом потенциальном силовом поле. Поэтому распределение (19.5) называют распределение Больцмана.
Пример 19.1. Пусть η0 — отношение концентрации молекул водорода к концентрации молекул азота вблизи поверхности Земли, а η — соответствующее отношение на высоте h = 3 км. Найти отношение η/η0 при  , полагая, что температура и ускорение свободного падения не зависят от высоты.
, полагая, что температура и ускорение свободного падения не зависят от высоты.
Дано:

| Решение

|
| η/η0 –? |

Ответ: η/η0 = 1,39.
Явления переноса
Назовем состояние газа неравновесным, если параметры газа при отсутствии внешних воздействий изменяются с течением времени. Изменение параметров состояния может происходить, например, из-за различия плотности и температуры газа в разных частях объема сосуда, в котором газ находится. Вследствие этого различия в газе наряду с хаотическим движением молекул происходит их упорядоченное движение из одной части объема газа в другую. Если не поддерживать внешним воздействием различий плотности и температуры, то с течением времени в результате упорядоченного движения молекул происходит выравнивание этих различий. Другими словами, газ при отсутствии внешних воздействий переходит из неравновесного состояния в равновесное.
В результате упорядоченного движения молекул в газе происходит перенос таких физических величин, как массы, внутренней энергии, импульса. Процессы, связанные с переносом физических величин в объеме вещества, называют явлениями переноса. К явлениям переноса относятся диффузия (перенос массы), теплопроводность (перенос внутренней энергии), внутреннее трение (перенос импульса).
Диффузия возникает вследствие неодинаковой плотности в различных частях объема газа.
Диффузией называют перенос массы газа из мест, где плотность его больше, в места, где плотность его меньше.
Допустим, что перенос массы происходит по оси 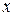 , т. е. плотность ρ газа есть функция только координаты
, т. е. плотность ρ газа есть функция только координаты 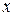 . Из опыта следует
. Из опыта следует
 |
(20.1)
где  — плотность потока массы (масса, переносимая в единицу времени через единицу площади
— плотность потока массы (масса, переносимая в единицу времени через единицу площади  , перпендикулярной оси
, перпендикулярной оси 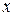 ),
), 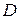 — коэффициент диффузии.
— коэффициент диффузии.
Знак минус показывает, что перенос массы происходит в направлении убывания плотности, т. е. по направлению оси 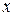 при
при  <
< 
 >
>  ) и в обратном направлении при
) и в обратном направлении при  >
>  (
( <
<  ).
).
Выражение (20.1) называют уравнением диффузии или законом Фика.
Теплопроводность возникает вследствие неодинаковой температуры в различных частях объема газа. Быстрые молекулы, попадая из теплых частей объема газа в холодные, отдают при столкновениях часть своей энергии медленным молекулам. Наоборот, медленные молекулы, попадая из холодных частей объема газа в теплые, отбирают при столкновениях часть энергии у быстрых молекул.
Теплопроводностью называют перенос внутренней энергии газа от теплых частей объема газа в холодные части объема.
Допустим, что перенос внутренней энергии происходит по оси 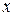 , т. е. температура
, т. е. температура 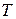 газа есть функция только координаты
газа есть функция только координаты 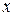 . Из опыта следует
. Из опыта следует
 æ
æ  (20.2)
(20.2)
где  — плотность потока тепла (количество тепла, переносимого в единицу времени через единицу площади
— плотность потока тепла (количество тепла, переносимого в единицу времени через единицу площади  , перпендикулярной оси
, перпендикулярной оси 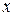 ), æ — коэффициент теплопроводности.
), æ — коэффициент теплопроводности.
Знак минус показывает, что перенос внутренней энергии происходит в направлении убывания температуры, т. е. по направлению оси 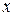 при
при  < <
< < 
 >
>  ) и в обратном направлении при
) и в обратном направлении при  >
> 
 <
< 
Выражение (20.2) называют уравнением теплопроводности или законом Фурье.
Внутреннее трение (вязкость) связано с возникновением сил трения между слоями газа, перемещающимися относительно друг друга с различными по модулю скоростями  . Молекулы, попадая из медленного слоя газа в быстрый, ускоряют при столкновениях свое упорядоченное движение. Наоборот, молекулы, попадая из быстрого слоя газа в медленный, замедляют при столкновениях свое упорядоченное движение.
. Молекулы, попадая из медленного слоя газа в быстрый, ускоряют при столкновениях свое упорядоченное движение. Наоборот, молекулы, попадая из быстрого слоя газа в медленный, замедляют при столкновениях свое упорядоченное движение.
Внутренним трением называют перенос молекулами результирующего импульса своего упорядоченного движения от быстрого слоя к медленному. В результате чего между слоями возникают силы трения, направленные по касательной к поверхности соприкосновения слоев.
Из опыта следует
 |
(20.3)
где τ — напряжение трения (сила трения, действующая на единицу площади поверхности слоя), η — коэффициент внутреннего трения (вязкости).
В выражениях (20.3)  — приращение модуля скорости течения газа при перемещении
— приращение модуля скорости течения газа при перемещении 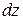 по оси
по оси  , перпендикулярной слоям и направленной в сторону более быстрого слоя. Так как
, перпендикулярной слоям и направленной в сторону более быстрого слоя. Так как 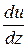 >
>  , то τ <
, то τ <  , т. е. направление силы трения противоположно направлению скорости течения газа.
, т. е. направление силы трения противоположно направлению скорости течения газа.
Выражение (20.3) называют уравнением внутреннего трения или законом Ньютона.
ГЛАВА 7. ТЕРМОДИНАМИКА
|
|
|


