 |
Второй и третий законы термодинамики
|
|
|
|
Назовем термодинамическую систему изолированной, если она не обменивается с внешней средой ни энергией, ни веществом. Из определения энтропии по Больцману (25.2) видно, что энтропия изолированной системы при равновесных обратимых процессах остается постоянной и равна максимальному значению:
Это видно и из определения энтропии по Клаузиусу (25.7). При 
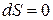, т. е. S = const.
При необратимом процессе, когда изолированная система переходит из неравновесного состояния в равновесное, энтропия системы возрастает. Действительно, так как
то из неравенства
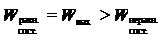
видно, что
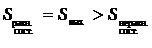
Возрастание энтропии при необратимом процессе видно и из выражения (25.8). При 
Из вышесказанного следует, что энтропии изолированной системы может только возрастать:
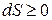(26.1)
Это утверждение называют законом возрастания энтропии или вторым законом термодинамики.
При температуре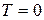 
любая система находится в основном состоянии, термодинамическая вероятность которого 
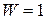. При этом
Отсюда можно сказать, что энтропия всякой системы стремится к нулю при стремлении к нулю температуры:
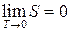(26.2)
Это утверждение называют теоремой Нериста или третьим законом термодинамики.
ГЛАВА 8. РЕАЛЬНЫЕ ГАЗЫ
Силы межмолекулярного взаимодействия в газах
Поведение молекул реальных газов отлично от поведения молекул газа. В реальных газах молекулы взаимодействуют друг с другом. Между молекулами одновременно существуют силы взаимного притяжения и силы взаимного отталкивания.
Различают три типа сил взаимного притяжения молекул: ориентационные, индукционные и дисперсионные. Все они имеют электрическую природу. Ориентационные силы притяжения действуют между полярными молекулами, индукционные — между полярной и неполярной молекулами, а дисперсионные — между неполярными молекулами, а также между любыми другими парами молекул.
|
|
|
Силы взаимного отталкивания молекул проявляются на очень малых расстояниях, когда перекрываются электронные оболочки молекул. Существование этих сил объясняется в квантовой механике на основании принципа Паули.
Силы межмолекулярного взаимодействия в сильной степени зависят от расстояния между молекулами. Рассмотрим две молекулы газа. Одну из них будем условно считать неподвижной. Поместим ее в точку 
, являющейся началом декартовых координат. Положение другой движущейся молекулы будем задавать с помощью радиус-вектора 
, проведенного из точки . На движущуюся молекулу со стороны неподвижной молекулы будут действовать одновременно две силы: сила отталкивания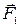 
и сила притяжения 
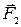, причем
, 
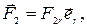(27.1)
где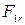 
и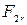 
— проекции сил 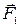и 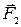на направление радиус-вектора 
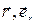— единичный вектор радиус-вектора .
Проекции сил 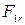и 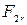зависят от расстояния 
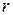между взаимодействующими молекулами. Расчет дает
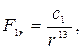
(27.2)
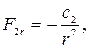(27.3)
где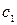 
и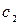 
— постоянные положительные коэффициенты, зависящие от химического состава молекул газа.
Результирующая сила межмолекулярного взаимодействия
где
(27.4)
— проекция силы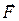 
на направление радиус-вектора .
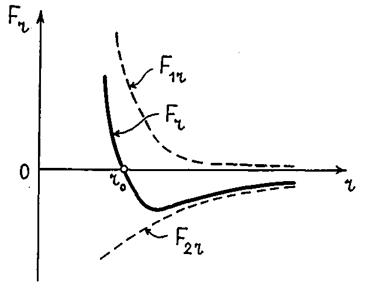
Изобразим графически зависимости (27.2)–(27.4) (рис 27.1).
|
Рис. 27.1
Из рис. 27.1 видно, что при 
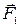силы и 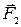взаимно уравновешиваются и результирующая сила 
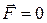. Если 
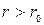, то преобладают силы взаимного притяжения, если 
— преобладают силы отталкивания. Таким образом,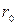 
— это то равновесие расстояние между молекулами, на котором они находились бы при отсутствии теплового движения, нарушающего это равновесие.
|
|
|
