 |
Теплоемкость идеального газа
|
|
|
|
Различные тела, обладающие одной и той же массой, нагреваются по-разному при сообщении им одного и того же количества тепла. Говорят, что они различаются теплоемкостями.
Теплоемкостью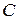 
тела называют величину, равную количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на один кельвин. Можем написать
(23.1)
где 
— количество тепла, которое нужно сообщить телу, чтобы увеличить его температуру на 
.
Теплоемкость одного килограмма тела называют удельной теплоемкостью. Можем написать
(23.2)
где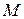 
— масса тела.
Теплоемкость одного моля тела называют молярной теплоемкостью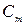 
. Можем написать
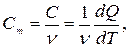(23.3)
где 
— число молей тела.
Теплоемкость зависит от условий, при которых происходит нагревание тела. Например, нагревание тела можно проводить при постоянном объеме или при постоянном давлении. В первом случае имеем теплоемкость 
при постоянном объеме, во втором — теплоемкость CP при постоянном давлении.
Получим выражение для теплоемкостей и CP идеального газа.
Пусть нагревание газа происходит при постоянном объеме (V = const) В этом случае газ не совершает работу над внешними телами 
. Первый закон термодинамики (23.3) имеет вид
(23.4)
С учетом соотношения (23.4) имеем
(23.5)
Внутренняя энергия идеального газа (см. § 16)
откуда, дифференцируя, получаем
(23.6)
Подставляя выражение (23.6) в соотношение (23.5), получаем теплоемкость идеального газа при постоянном объеме
(23.7)
Молярная теплоемкость идеального газа при постоянном объеме
(23.8)
Теперь рассмотрим нагревание газа при постоянном давлении (P = const). Разделим соотношение (22.3) на :
|
|
|
(23.9)
С учетом формулы (23.5)
(23.10)
Продифференцируем уравнение Клапейрона–Менделеева
при P = const:
откуда
 |
(23.11)
По определению теплоемкости (16.1)
 |
(23.12)
Подставляя выражения (23.10)–(23.12) в соотношение (23.9), получаем теплоемкость идеального газа при постоянном давлении
 |
(23.13)
Из соотношения (23.13) видно, что теплоемкость газа при постоянном давлении больше теплоемкости газа при постоянном объеме. Это объясняется тем, что при нагревании газа при постоянном объеме все подведенное к газу количество тепла идет только на увеличение внутренней энергии, а при нагревании газа при постоянном давлении подведенное к газу количество тепла расходуется не только на увеличение внутренней энергии, но и на работу, совершаемую газом при расширении.
Молярная теплоемкость идеального газа при постоянном давлении
(23.14)
Соотношение (23.14) называют уравнением Майера. С учетом выражения (23.8) имеем
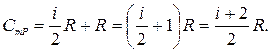
(23.15)
Пример 23.1. При изотермическом расширении ν молей идеального газа при температуре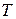 
его объем увеличился от 
до 
. Определить количество тепла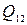 
. полученное газом.
Дано:
| Решение
|
|
Ответ: 
Пример 23.2. Какое количество тепла 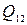надо сообщить водороду массой M = 100 г для изохорного нагревания на 
?
| Дано:
M = 100 г
| Решение
|
|
|
Ответ: 
Адиабатический процесс
Адиабатическим называют процесс, в котором система не обменивается теплотой с внешней средой 
.
Найдем связь между давлением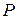 
и объемом 
идеального газа в адиабатическом процессе.
Дифференцируя уравнение Клапейрона–Менделеева
 |
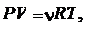получаем
 |
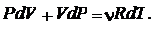(24.1)
Из первого закона термодинамики (22.3) при 
следует с учетом выражений (22.6), (23.6) и (23.8)
откуда
 |
|
|
|
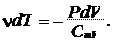(24.2)
Подставляя выражение (24.2) в соотношение (24.1), имеем
откуда с учетом уравнения Майера (23.14)
(24.3)
Разделим уравнение (24.3) на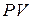 
и проинтегрируем:
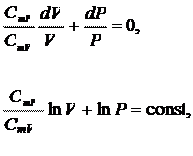
откуда
или
 |
(24.4)
где 
Уравнение (24.4) называют уравнением Пуассона,а безразмерную величину γ — коэффициентом Пуассона или показателем адиабаты. С учетом выражений (23.8) и (23.15)
 |
(24.5)
Кривую, изображающую адиабатический процесс, называют адиабатой (рис. 24.1).
|
Рис. 24.1
Практически адиабатический процесс осуществляется при быстром расширении или сжатии газа.
Пример 24.1. Один моль кислорода, находившегося при температуре 
адиабатически сжали так, что его давление возросло в 
раз. Найти работу 
, которая была совершена над газом.
Дано:
| Решение
|
|
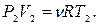
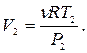
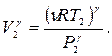
Ответ: 
Энтропия
Набором макроскопичесих параметров, например, 
и 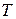, задается состояние системы в целом или макросостояние системы. Набор параметров и 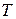выражает осредненное суммарное состояние большого числа молекул, из которых состоит система. Назовем микросостоянием системы состояние всех молекул, образующих систему. Состояние каждой молекулы определяется заданием ее координат и скорости в данный момент времени. Очевидно, что микросостояние системы непрерывно меняется. Однако набор макроскопических параметров и 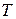, а, следовательно, и макросостояние системы при этом может не меняться. Назовем термодинамической вероятностью 
число различных микросостояний, соответствующих данному макросостоянию.
Вероятность макросостояния пропорциональна его термодинамической вероятности. Для равновесного состояния системы, при котором параметры 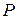, , и 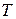остаются неизменными, имеет максимальное значение по сравнению с любым неравновесным состоянием. Поэтому равновесное состояние наиболее вероятно. Если система переходит из неравновесного состояния в равновесное, то такой процесс необратим.
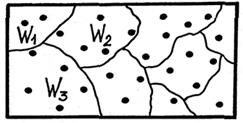
Определить вероятность состояния через термодинамическую вероятность неудобно, так как не обладает свойством аддитивности (нельзя складывать). Действительно, если мысленно разбить термодинамическую систему на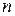 
подсистем с термодинамическими вероятностями 
(рис 25.1), то
|
|
|
|
Рис. 25.1
термодинамическая вероятность системы
(25.1)
откуда видно, что не является аддитивной величиной.
Взяв логарифм от соотношения (25.1), получим
откуда видно, что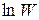 
— аддитивная величина (можно складывать).
Введем физическую величину
(25.2)
где 
— постоянная Больцмана. Величину 
называют энтропией системы. Она характеризует вероятность макросостояния системы. Определение энтропии (25.2) было сделано Больцманом.
Дадим еще одно определение энтропии. Рассмотрим расширение газа в пустоту (рис. 25.2).
|
Рис. 25.2
Расчет дает
где 
— число молекул газа в объеме , или
,
где 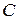— коэффициент пропорциональности.
Очевидно, в нашем случае 
, так как 
. С учетом выражения (25.2) можем написать
откуда приращение энтропии
(25.3)
Учитывая, что 
и 
, перепишем выражение (25.3) в виде
 |
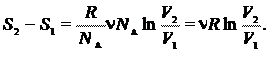(25.4)
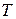При изотермическом увеличении объема газа от до при температуре количество тепла, полученное газом,
 |
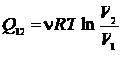(25.5)
(см. пример 23.1). Сравнивая выражение (25.4) и (25.5), получаем
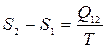
(25.6)
или для элементарного приращения энтропии
(25.7)
Формула (25.7) верна не только для изотермического процесса, но и для любого равновесного обратимого процесса
(25.8)
Определение энтропии (25.7) было сделано Клаузиусом.
Из выражений (25.2) и (25.6) следует, что энтропия является функцией состояния системы.
Пример 25.1. Определить приращение энтропии 
при изотермическом кислорода массой M = 10 г от объема V 1 = 25 л до объема V 2 = 100 л.
| Дано: M = 10 г V 1 = 25 л V 2 = 100 л | Решение
|
|
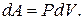
Ответ: 
Пример 25.2. Пять молей гелия изохорически переводят из состояния, в котором его давление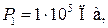 
в состояние, в котором его давление 
Определить приращение энтропии 
гелия.
Дано:
| Решение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 
|
|
|
