 |
Плоскость и прямая в пространстве
|
|
|
|
Л.Г.Корсакова
ВЫСШАЯ МАТЕМАТИКА
ДЛЯ МЕНЕДЖЕРОВ
Калининград
Г.
Л.Г.Корсакова
ВЫСШАЯ МАТЕМАТИКА
ДЛЯ МЕНЕДЖЕРОВ
Учебное пособие
Калининград
2004 г.
УДК 512.64: 514.12: (517.2 + 517.3)
Л.Г.Корсакова. Высшая математика для менеджеров: Учебное пособие. - Калинингр. ун-т. - Калининград,2004 г.. - 04 с. - ISBN 5-88874-044-6.
Рассматриваются основные понятия высшей математики, которые являются базой математического инструментария современного менеджмента.
Приводятся краткие теоретические сведения по аналитической геометрии, линейной алгебре и математическому анализу и их применение при решении прикладных задач в экономике и управлении. Рассмотрены решения типовых задач, отражающих специфику экономических расчетов.
Пособие предназначено для студентов-менеджеров заочного обучения. Может быть также полезно и для студентов дневного отделения.
Печатается по решению редакционно-издательского Совета Калининградского государственного университета.
Рецензенты: профессор Афинского университета экономики и бизнеса, доктор экономики Т.Скурас; профессор Афинского университета экономики и бизнеса, доктор экономики А.Харламбиду.
ISBN 5-88874-044-6 Ó Калининградский государственный университет, 2004 г.
ПРЕДИСЛОВИЕ
Учебное пособие “Высшая математика для менеджеров” включает такие разделы высшей математики, изучение которых дает математический аппарат, наиболее активно применяемый для решения прикладных экономических и управленческих задач. Это аналитическая геометрия, линейная алгебра и математический анализ.
Знание аналитической геометрии необходимо современному менеджеру, чтобы грамотно толковать экономическую информацию, представляемую в виде различных графиков - это кривые и поверхности безразличия, кривые потребительского бюджета, инвестиционного спроса, кривые Филлипса, Лаффера, Лоренца и т. д.; выводить интерполяционные формулы по методу наименьших квадратов; находить наилучший план производства при заданных ресурсах.
|
|
|
В разделе “Линейная алгебра” основное внимание уделяется матрицам, определителям и системам линейных уравнений, поскольку в экономических исследованиях широко используются различные матричные модели - межотраслевого баланса, в плановых расчетах, при расчетах фонда заработной платы и т.д. Линейные модели, сводящиеся к системам алгебраических линейных уравнений или неравенств, c достаточно высокой точностью соответствуют описываемым ими явлениям; с их помощью решаются многие управленческие задачи.
Математический анализ дает ряд фундаментальных понятий, которыми оперирует экономист, - это функция, предел, производная, интеграл, дифференциальное уравнение. Например, второй замечательный предел применяется при решении задач о росте банковского вклада по закону сложных процентов; использование понятия производной приводит к такой специальной дисциплине, как предельный анализ в экономике и т.д.
В начале каждого параграфа приводятся краткие сведения из теории, носящие справочный характер. Основное внимание уделяется практическому освоению студентами изучаемого материала. Для достижения этой цели приводится большое число упражнений. Их выполнение будет способствовать выработке навыков рационального решения типовых примеров и задач, а также задач экономического и производственного содержания, развивающих навыки применения изученного математического инструментария. Задания для самостоятельных индивидуальных работ предлагаются в книге: Корсакова Л.Г. Математика для экономистов в примерах и задачах: Учеб.пособие/ Калинингр. ун-т. - Калининград, 1994.
|
|
|
В конце пособия приводится список литературы, в который вошли все источники, использованные в той или иной мере при его написании.
Автор выражает глубокую благодарность рецензентам - профессорам Афинского университета экономики и бизнеса Танасу Скурасу и Анике Харламбиду, а также доценту кафедры вычислительной математики Л. В. Зинину, коллегам по математическому факультету за ценные замечания и помощь при подготовке пособия.
I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Векторы
Упорядоченную совокупность (x1, x2,..., x n) n вещественных чисел называют n-мерным вектором, а числа xi (i =  ) - компонентами, или координатами, вектора.
) - компонентами, или координатами, вектора.
Если, например, некоторый автомобильный завод должен выпустить в смену 50 легковых автомобилей, 100 грузовых, 10 автобусов, 50 комплектов запчастей для легковых автомобилей и 150 комплектов для грузовых автомобилей и автобусов, то производственную программу этого завода можно записать в виде вектора (50, 100, 10, 50, 150), имеющего пять компонент. Векторы обозначают жирными строчными буквами или буквами с чертой или стрелкой наверху, например, a или `a. Два вектора называются равными, если они имеют одинаковое число компонент и их соответствующие компоненты равны.
Компоненты вектора нельзя менять местами, например, (3, 2, 5, 0, 1) ¹
¹ (2, 3, 5, 0, 1).
Произведением вектора x = (x1, x2,...,xn) на действительное число l называется вектор l x = (l x1, l x2,..., l xn).
Суммой векторов x = (x1, x2,...,xn) и y = (y1, y2,...,yn) называется вектор x + y = (x1 + y1, x2 + y2,..., x n + yn).
N - мерное векторное пространство R nопределяется как множество всех n-мерных векторов, для которых определены операции умножения на действительные числа и сложение.
Экономическая иллюстрация n-мерного векторного пространства: пространство благ (товаров). Под товаром мы будем понимать некоторое благо или услугу, поступившие в продажу в определенное время в определенном месте. Предположим, что существует конечное число наличных товаров n; количества каждого из них, приобретенные потребителем, характеризуются набором товаров
x = (x1, x2,..., xn),
где через xi обозначается количество i-го блага, приобретенного потребителем. Будем считать, что все товары обладают свойством произвольной делимости, так что может быть куплено любое неотрицательное количество каждого из них. Тогда все возможные наборы товаров являются векторами пространства товаров C = { x = (x1, x2,..., xn) ê xi ³ 0, i =  }.
}.
|
|
|
Система e 1, e 2,..., e m n-мерных векторов называется линейно зависимой, если найдутся такие числа l1, l2,..., lm, из которых хотя бы одно отлично от нуля, что выполняется равенство l1 e 1 + l2 e 2 +... + lm e m = 0; в противном случае данная система векторов называется линейно независимой, то есть указанное равенство возможно лишь в случае, когда все l1 = l2 =... =
= lm = 0. Геометрический смысл линейной зависимости векторов в R 3, интерпретируемых как направленные отрезки, поясняют следующие теоремы.
Теорема 1. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.
Теорема 2. Для того, чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.
Теорема 3. Для того, чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.
Тройка некомпланарных векторов a, b, c называется правой, если наблюдателю из их общего начала обход концов векторов a, b, c в указанном порядке кажется совершающимся по часовой стрелке. B противном случае a, b, c - левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными.
Тройка e 1, e 2, e 3 некомпланарных векторов в R 3 называется базисом, а сами векторы e 1, e 2, e 3 - базисными. Любой вектор a может быть единственным образом разложен по базисным векторам, то есть представлен в виде
а = x1 e 1 + x2 e 2 + x3 e 3, (1.1)
числа x1, x2, x3 в разложении (1.1) называются координатами вектора a в базисе e 1, e 2, e 3 и обозначаются a (x1, x2, x3). Если векторы e 1, e 2, e 3 попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x1, x2, x3 - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать i, j, k.
Будем предполагать, что в пространстве R 3 выбрана правая система декартовых прямоугольных координат {0, i, j, k }.
|
|
|
Векторным произведением вектора а на вектор b называется вектор c, который определяется следующими тремя условиями:
1. Длина вектора c численно равна площади параллелограмма, построенного на векторах a и b, т. е. ê c ê = êa ê êb êsin (a ^ b).
2. Вектор c перпендикулярен к каждому из векторов a и b.
3. Векторы a, b и c, взятые в указанном порядке, образуют правую тройку.
Для векторного произведения c вводится обозначение c = [ ab ] или
c = a´ b.
Если векторы a и b коллинеарны, то sin(a^b) = 0 и [ ab ] = 0, в частности, [ aa ] = 0. Векторные произведения ортов: [ ij ]= k, [ jk ] = i, [ ki ]= j.
Если векторы a и b заданы в базисе i, j, k координатами a (a1, a2, a3), b (b1, b2, b3), то
[ ab ] =  =`i (a2b3 - a3b2) - `j (a1b3 - a3b1) + `k (a1b2 - a2b1).
=`i (a2b3 - a3b2) - `j (a1b3 - a3b1) + `k (a1b2 - a2b1).
Если векторное произведение двух векторов а и b скалярноумножается на третий вектор c, то такое произведение трех векторов называется смешанным произведением и обозначается символом a b c.
Если векторы a, b и c в базисе i, j, k заданы своими координатами
a (a1, a2, a3), b (b1, b2, b3), c (c1, c2, c3), то
abc =  .
.
Смешанное произведение имеет простое геометрическое толкование - это скаляр, по абсолютной величине равный объему параллелепипеда, построенного на трех данных векторах.
Если векторы образуют правую тройку, то их смешанное произведение есть число положительное, равное указанному объему; если же тройка
a, b, c - левая, то a b c <0 и V = - a b c, следовательно V = ê a b c ê.
Координаты векторов, встречающиеся в задачах первой главы, предполагаются заданными относительно правого ортонормированного базиса. Единичный вектор, сонаправленный вектору а, обозначается символом а о. Символом r = ОМ обозначается радиус-вектор точки М, символами а, АВ или ê а ê, ê АВ ê обозначаются модули векторов а и АВ.
Пример 1.1. Зная векторы a и b, на которых построен параллелограмм, выразить через них вектор, совпадающий с высотой параллелограмма, перпендикулярной к стороне a.
Решение. Обозначим AB = a, AC = b, CD = h, где CD ^ a, D-основание пер-
C
b h
D a
А B      Рис. 1.
Рис. 1.
| пендикуляра, опущенного из точки C на сторону a. По правилу сложения векторов имеем: b + h = AD, h = AD - b.ПосколькуADçça, то AD = l a. Найдем значение l, используя ортогональность векторов a иh:ah=0 или a(la-b)=0, откуда l = ab /a2. Следовательно, h = (ab /a2)a - b. |
Пример 1.2. Найдите угол между векторами a = 2 m +4 n и b = m-n, где m и n -единичные векторы и угол между m и n равен 120о.
Решение. Имеем: cos j = ab /ab, ab = (2 m +4 n) (m-n) = 2 m 2 - 4 n 2 +2 mn =
= 2 - 4+2cos120o = - 2 + 2(-0.5) = -3; a =  ; a 2 = (2 m +4 n) (2 m +4 n) =
; a 2 = (2 m +4 n) (2 m +4 n) =
= 4 m 2 +16 mn +16 n 2 = 4+16(-0.5)+16=12, значит a =  . b =
. b =  ; b 2 =
; b 2 =
= (m-n)(m-n) = m 2 -2 mn + n 2 = 1-2(-0.5)+1 = 3, значит b =  . Окончательно имеем: cos j =
. Окончательно имеем: cos j =  = -1/2, Þ j = 120o.
= -1/2, Þ j = 120o.
|
|
|
Пример 1.3. Зная векторы AB (-3,-2,6) и BC (-2,4,4),вычислите длину высоты AD треугольника ABC.
Решение. Обозначая площадь треугольника ABC через S, получим:
S = 1/2 BC AD. Тогда AD=2S/BC, BC= 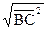 =
=  = 6,
= 6,
S = 1/2 ç AB ´ACç. AC=AB+BC, значит, вектор AC имеет координаты
AC (-5,2,10). AB´AC =  = i (-20 -12) - j (30 -30) + k (- 6 - 10) =
= i (-20 -12) - j (30 -30) + k (- 6 - 10) =
= -16(2`i +`k). ç AB´ACç =  = 16
= 16 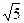 ; S = 8
; S = 8 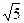 , откуда
, откуда
AD =  =
=  .
.
Пример 1.4. Даны два вектора a (11,10,2) и b (4,0,3). Найдите единичный вектор c, ортогональный векторам a и b и направленный так, чтобы упорядоченная тройка векторов a, b, c была правой.
Решение. Обозначим координаты вектора c относительно данного правого ортонормированного базиса через x, y, z.
Поскольку c ^ a, c ^ b, то ca = 0, cb = 0. По условию задачи требуется, чтобы c = 1 и a b c >0.
Имеем систему уравнений для нахождения x,y,z: 11x +10y + 2z = 0, 4x+3z=0, x2 + y2 + z2 = 0.
Из первого и второго уравнений системы получим z = -4/3 x, y = -5/6 x. Подставляя y и z в третье уравнение, будем иметь: x2 = 36/125, откуда
x = ±  . Используя условие a b c > 0, получим неравенство
. Используя условие a b c > 0, получим неравенство
 > 0 или 5(6x-5y-8z) > 0.
> 0 или 5(6x-5y-8z) > 0.
С учетом выражений для z и y перепишем полученное неравенство в виде: 625/6 x > 0, откуда следует, что x>0. Итак, x =  , y = -
, y = -  , z =-
, z =-  .
.
Линии на плоскости
При чтении экономической литературы приходится иметь дело с большим количеством графиков. Укажем некоторые из них.
Кривая безразличия - кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета - кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей - кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса - кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.
Кривая Филлипса - кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.
Кривая Лаффера - кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.
Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и разбираться в свойствах простейших кривых, каковыми являются прямые линии и кривые второго порядка - окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной системой неравенств.
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F(x,y)=0. При этом на функцию F должны быть наложены ограничения так, чтобы, с одной стороны, это уравнение имело бесконечное множество решений и, с другой стороны, чтобы это множество решений не заполняло “куска плоскости”. Важный класс линий составляют те, для которых функция F(x,y) есть многочлен от двух переменных, в этом случае линия, определяемая уравнением F(x,y)=0, называется алгебраической. Алгебраические линии, задаваемые уравнением первой степени, cуть прямые. Уравнение второй степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или линию, распадающуюся на две прямые.
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
10. Общее уравнение прямой:
Ax + By + C = 0. (2.1)
Вектор n (А,В) ортогонален прямой, числа A и B одновременно не равны нулю.
20. Уравнение прямой с угловым коэффициентом:
y - yo = k (x - xo), (2.2)
где k - угловой коэффициент прямой, то есть k = tg a, где a - величина угла, образованного прямой с осью Оx, M (xo, yo) - некоторая точка, принадлежащая прямой.
Уравнение (2.2) принимает вид y = kx + b, если M (0, b) есть точка пересечения прямой с осью Оy.
30. Уравнение прямой в отрезках:
x/a + y/b = 1, (2.3)
где a и b - величины отрезков, отсекаемых прямой на осях координат.
40. Уравнение прямой, проходящей через две данные точки - A(x1, y1) и B(x2, y2):
 . (2.4)
. (2.4)
50. Уравнение прямой, проходящей через данную точку A(x1, y1) параллельно данному вектору a (m, n):
 . (2.5)
. (2.5)
60. Нормальное уравнение прямой:
rn о - р = 0, (2.6)
где r - радиус-вектор произвольной точки M(x, y) этой прямой, n о- единичный вектор, ортогональный этой прямой и направленный от начала координат к прямой; р - расстояние от начала координат до прямой.
Нормальное уравнение прямой в координатной форме имеет вид:
x cos a + y sin a - р = 0,
где a - величина угла, образованного прямой с осью Оx.
Уравнение пучка прямых с центром в точке А(x1, y1) имеет вид:
y-y1 = l(x-x1),
где l - параметр пучка. Если пучок задается двумя пересекающимися прямыми A1 x + B1 y + C1= 0, A2 x + B2 y + C2 = 0, то его уравнение имеет вид:
l (A1 x + B1 y + C1) + m (A2 x + B2 y + C2)=0,
где l и m - параметры пучка, не обращающиеся в 0 одновременно.
Величина угла между прямыми y = kx + b и y = k1 x + b1 задается формулой:
tg j =  .
.
Равенство 1 + k1 k = 0 есть необходимое и достаточное условие перпендикулярности прямых.
Для того, чтобы два уравнения
A1 x + B1 y + C1= 0, (2.7)
A2 x + B2 y + C2 = 0, (2.8)
задавали одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны:
A1/A2 = B1/B2 = C1/C2.
Уравнения (2.7), (2.8) задают две различные параллельные прямые, если A1/A2 = B1/B2 и B1/B2 ¹ C1/C2; прямые пересекаются, если A1/A2 ¹ B1/B2.
Расстояние d от точки Mо(xо, yо) до прямой есть длина перпендикуляра, проведенного из точки Mо к прямой. Если прямая задана нормальным уравнением, то d = ê r о n о - р ê, где r о - радиус-вектор точки Mо или, в координатной форме, d = êxо cosa + yо sina - р ê.
Общее уравнение кривой второго порядка имеет вид:
a11x2 + 2a12xy + a22y2 + 2a1x +2a2y +a = 0.
Предполагается, что среди коэффициентов a11, a12, a22 есть отличные от нуля.
Уравнение окружности с центром в точке С(a, b) и радиусом, равным R:
(x - a)2 + (y - b)2 = R2. (2.9)
Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек F1 и F2 (фокусов) есть величина постоянная, равная 2a.
Каноническое (простейшее) уравнение эллипса:
x2/a2 + y2/a2 = 1. (2.10)
Эллипс, заданный уравнением (2.10), симметричен относительно осей координат. Параметры a и b называются полуосями эллипса.
Пусть a>b, тогда фокусы F1 и F2 находятся на оси Оx на расстоянии
c=  от начала координат. Отношение c/a = e < 1 называется эксцентриситетом эллипса. Расстояния от точки M(x, y) эллипса до его фокусов (фокальные радиусы-векторы) определяются формулами:
от начала координат. Отношение c/a = e < 1 называется эксцентриситетом эллипса. Расстояния от точки M(x, y) эллипса до его фокусов (фокальные радиусы-векторы) определяются формулами:
r1 = a - ex, r2 = a +ex.
Если же a < b, то фокусы находятся на оси Оy, c=  , e = c/b,
, e = c/b,
r1 = b + ex, r2 = b - ex.
Если a = b, то эллипс является окружностью с центром в начале координат радиуса a.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек F1 и F2 (фокусов) равна по абсолютной величине данному числу 2a.
Каноническое уравнение гиперболы:
x2/a2 - y2/b2 = 1. (2.11)
Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось Оx в точках A (a,0) и A (-a,0) - вершинах гиперболы и не пересекает ось Оy. Параметр a называется вещественной полуосью, b - мнимой полуосью. Параметр c=  есть расстояние от фокуса до начала координат. Отношение c/a = e >1 называется эксцентриситетом гиперболы. Прямые y = ± b/a x называются асимптотами гиперболы. Расстояния от точки M(x,y) гиперболы до ее фокусов (фокальные радиусы-векторы) определяются формулами:
есть расстояние от фокуса до начала координат. Отношение c/a = e >1 называется эксцентриситетом гиперболы. Прямые y = ± b/a x называются асимптотами гиперболы. Расстояния от точки M(x,y) гиперболы до ее фокусов (фокальные радиусы-векторы) определяются формулами:
r1 = êex - a ê, r2 = êex + a ê.
Гипербола, у которой a = b, называется равносторонней, ее уравнение x2 - y2 = a 2, а уравнение асимптот y = ± x. Гиперболы x2/a2 - y2/b2 = 1 и
y2/b2 - x2/a2 = 1 называются сопряженными.
Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).
Каноническое уравнение параболы имеет два вида:
1) y2 = 2рx - парабола симметрична относительно оси Оx.
2) x2 = 2рy - парабола симметрична относительно оси Оy.
В обоих случаях р>0 и вершина параболы, то есть точка, лежащая на оси симметрии, находится в начале координат.
Парабола y 2 = 2рx имеет фокус F(р/2,0) и директрису x = - р/2, фокальный радиус-вектор точки M(x,y) на ней r = x+ р/2.
Парабола x2 =2рy имеет фокус F(0, р/2) и директрису y = - р/2; фокальный радиус-вектор точки M(x,y) параболы равен r = y + р/2.
Уравнение F(x, y) = 0 задает линию, разбивающую плоскость на две или несколько частей. В одних из этих частей выполняется неравенство F(x, y)<0, а в других - неравенство F(x, y)>0. Иными словами, линия
F(x, y)=0 отделяет часть плоскости, где F(x, y)>0, от части плоскости, где F(x, y)<0.
Прямая Ax+By+C = 0 разбивает плоскость на две полуплоскости. На практике для выяснения того, в какой полуплоскости мы имеем Ax+By+C<0, а в какой Ax+By+C>0, применяют метод контрольных точек. Для этого берут контрольную точку (разумеется, не лежащую на прямой Ax+By+C = 0) и проверяют, какой знак имеет в этой точке выражение Ax+By+C. Тот же знак имеет указанное выражение и во всей полуплоскости, где лежит контрольная точка. Во второй полуплоскости Ax+By+C имеет противоположный знак.
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Например, решим неравенство x2-4x+y2+6y-12 > 0. Его можно переписать в виде (x-2)2 + (y+3)2 - 25 > 0.
Уравнение (x-2)2 + (y+3)2 - 25 = 0 задает окружность с центром в точке C(2,-3) и радиусом 5. Окружность разбивает плоскость на две части - внутреннюю и внешнюю. Чтобы узнать, в какой из них имеет место данное неравенство, возьмем контрольную точку во внутренней области, например, центр C(2,-3) нашей окружности. Подставляя координаты точки C в левую часть неравенства, получаем отрицательное число -25. Значит, и во всех точках, лежащих внутри окружности, выполняется неравенство
x2-4x+y2+6y-12 < 0. Отсюда следует, что данное неравенство имеет место во внешней для окружности области.
Пример 1.5. Составьте уравнения прямых, проходящих через точку A(3,1) и наклоненных к прямой 2x+3y-1 = 0 под углом 45o.
Решение. Будем искать уравнение прямой в виде y=kx+b. Поскольку прямая проходит через точку A, то ее координаты удовлетворяют уравнению прямой, т.е. 1=3k+b, Þ b=1-3k. Величина угла между прямыми
y= k1 x+b1 и y= kx+b определяется формулой tgj =  . Так как угловой коэффициент k1 исходной прямой 2x+3y-1=0 равен - 2/3, а угол j = 45o, то имеем уравнение для определения k:
. Так как угловой коэффициент k1 исходной прямой 2x+3y-1=0 равен - 2/3, а угол j = 45o, то имеем уравнение для определения k:
(2/3 + k)/(1 - 2/3k) = 1 или (2/3 + k)/(1 - 2/3k) = -1.
Имеем два значения k: k1 = 1/5, k2 = -5. Находя соответствующие значения b по формуле b=1-3k, получим две искомые прямые: x - 5y + 2 = 0 и
5x + y - 16 = 0.
Пример 1.6. При каком значении параметра t прямые, заданные уравнениями 3tx-8y+1 = 0 и (1+t)x-2ty = 0, параллельны?
Решение. Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 3t/(1+t) = -8/(-2t). Решая полученное уравнение, находим t: t1 = 2, t2 = -2/3.
Пример 1.7. Найти уравнение общей хорды двух окружностей:
x2 +y2 =10 и x2+y2-10x-10y+30=0.
Решение. Найдем точки пересечения окружностей, для этого решим систему уравнений:
 .
.
Решая первое уравнение, находим значения x1 = 3, x2 = 1. Из второго уравнения - соответствующие значения y: y1 = 1, y2 = 3. Теперь получим уравнение общей хорды, зная две точки А(3,1) и B(1,3), принадлежащие этой прямой: (y-1)/(3-1) = (x-3)/(1-3), или y+ x - 4 = 0.
Пример 1.8. Как расположены на плоскости точки, координаты которых удовлетворяют условиям (x-3) 2 + (y-3) 2 < 8, x > y?
Решение. Первое неравенство системы определяет внутренность круга, не включая границу, т.е. окружность с центром в точке (3,3) и радиуса  . Второе неравенство задает полуплоскость, определяемую прямой x = y, причем, так как неравенство строгое, точки самой прямой не принадлежат полуплоскости, а все точки ниже этой прямой принадлежат полуплоскости. Поскольку мы ищем точки, удовлетворяющие обоим неравенствам, то искомая область - внутренность полукруга.
. Второе неравенство задает полуплоскость, определяемую прямой x = y, причем, так как неравенство строгое, точки самой прямой не принадлежат полуплоскости, а все точки ниже этой прямой принадлежат полуплоскости. Поскольку мы ищем точки, удовлетворяющие обоим неравенствам, то искомая область - внутренность полукруга.
Пример 1.9. Вычислить длину стороны квадрата, вписанного в эллипс x2/a2 + y2/b2 = 1.
Решение. Пусть М(с, с) - вершина квадрата, лежащая в первой четверти. Тогда сторона квадрата будет равна 2 с. Т.к. точка М принадлежит эллипсу, ее координаты удовлетворяют уравнению эллипса c2/a2 + c2/b2 = 1, откуда
c = ab/  ; значит, сторона квадрата - 2ab/
; значит, сторона квадрата - 2ab/  .
.
Пример 1.10. Зная уравнение асимптот гиперболы y = ± 0,5 x и одну из ее точек М(12, 3  ), составить уравнение гиперболы.
), составить уравнение гиперболы.
Решение. Запишем каноническое уравнение гиперболы: x2/a2 - y2/b2 = 1. Асимптоты гиперболы задаются уравнениями y = ± 0,5 x, значит, b/a = 1/2, откуда a=2b. Поскольку М - точка гиперболы, то ее координаты удовлетворяют уравнению гиперболы, т.е. 144/a2 - 27/b2 = 1. Учитывая, что a = 2b, найдем b: b2=9 Þ b=3 и a=6. Тогда уравнение гиперболы - x2/36 - y2/9 = 1.
Пример 1.11. Вычислить длину стороны правильного треугольника ABC, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.
Решение. Каноническое уравнение параболы с параметром р имеет вид y2 = 2рx, вершина ее совпадает с началом координат, и парабола симметрична относительно оси абсцисс. Так как прямая AB образует с осью Ox угол в 30o, то уравнение прямой имеет вид: y = 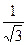 x.
x.
Следовательно, мы можем найти координаты точки B, решая систему уравнений y2=2рx, y = 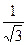 x, откуда x = 6р, y = 2
x, откуда x = 6р, y = 2  р. Значит, расстояние между точками A(0,0) и B(6р,2
р. Значит, расстояние между точками A(0,0) и B(6р,2  р) равно 4
р) равно 4  р.
р.
Пример 1.12. Со станции ежедневно можно отправлять пассажирские и скорые поезда. Данные приведены в таблице.
| Тип поезда | Количество вагонов в составе | ||
| плацкартных | купейных | мягких | |
| Пассажирский | |||
| Скорый | |||
| Резерв вагонов |
Записать в математической форме условия, не позволяющие превысить наличный парк вагонов при формировании пассажирских и скорых поездов, ежедневно отправляемых со станции. Построить на плоскости Oxy область допустимых вариантов формирования поездов.
Решение. Обозначим через x количество пассажирских поездов,
а через y - количество скорых. Получим систему линейных неравенств:
5x + 8y £ 80, 6x + 4y £ 72, 3x + y £ 21, x ³ 0, y ³ 0.
Построим соответствующие прямые:
5x + 8y = 80, 6x +4y = 72, 3x + y = 21, x = 0, y = 0,
записав их уравнения в виде уравнений прямых в отрезках: x/16 + y/10 = 1, x/12 + y/18 = 1, x/7 + y/21 = 1, x = 0, y = 0.
Заштрихуем полуплоскости, удовлетворяющие данным неравенствам, и получим область допустимых значений:
 y
y
 21
21
 18
18
 10
10
 | |||||||
 | |||||||
 | |||||||
 |




































 0 7 12 16 x
0 7 12 16 x
Рис. 2
.
Итак, количество скорых поездов не превышает 10, а пассажирских должно быть не более 7.
Пример 1.13. Имеются два пункта производства (A и B) некоторого вида продукции и три пункта (I, II, III) его потребления. В пункте А производится 250 единиц продукции, а в пункте В - 350 единиц. В пункте I требуется 150 единиц, в пункте II -240 единиц и в пункте III - 210 единиц. Стоимость перевозки одной единицы продукции из пункта производства в пункт потребления дается следующей таблицей.
Таблица 1
| Пункт | Пункт потребления | ||
| производства | I | II | III |
| A | |||
| B |
Требуется составить план перевозки продукции, при котором сумма расходов на перевозку будет наименьшей.
Решение. Обозначим количество продукции, перевозимой из пункта А в пункт I через x, а из пункта А в пункт II - через y. Так как полная потребность в пункте I равна 150 единицам, то из пункта В надо завезти (150 - x) единиц. Точно так же из пункта В в пункт II надо завезти (240 - y) единиц. Далее: производительность пункта А равна 250 единицам, а мы уже распределили (x + y) единиц. Значит, в пункт III идет из пункта А (250 - x -y) единиц. Чтобы полностью обеспечить потребность пункта III, осталось завезти 210 - (250 - x -y) = x + y - 40 единиц из пункта В. Итак, план перевозок задается следующей таблицей.
Таблица 2
| Пункт | Пункт потребления | ||
| производства | I | II | III |
| A | x | y | 250 - x - y |
| B | 150 - x | 240 - y | x + y - 40 |
Чтобы найти полную стоимость перевозки, надо умножить каждый элемент этой таблицы на соответствующий элемент предыдущей таблицы и сложить полученные произведения. Получим выражение:
S(x,y) = 4x + 3y + 5 (250 - x - y) + 5 (150 - x) +
+ 6 (240 -y) + 4 (x + y - 40) = - 2x - 4y +3280.
По условию задачи требуется найти минимум этого выражения. Но величины x и y не могут принимать произвольных значений. Ведь количество перевозимой продукции не может быть отрицательным. Поэтому все числа таблицы 2 неотрицательны:
x ³ 0, y ³ 0, 250 - x - y ³ 0, 150 -x ³ 0, 240 - y ³ 0, x + y - 40 ³ 0. (2.12)
Итак, нам надо найти минимум функции S(x,y) в области, задаваемой системой неравен
|
|
|


