 |
Частные производные. Метод наименьших квадратов
|
|
|
|
Пусть D(x, y) - некоторое множество точек плоскости Oxy. Если каждой упорядоченной паре чисел (x, y) из области D соответствует определенное число z Î Z Ì R, то говорят, что z есть функция двух независимых переменных x и y. Переменные x и y называются независимыми переменными, или аргументами, D - областью определения, или существования, функции, а множество Z всех значений функции - областью ее значений. Функциональную зависимость z от x и y записывают в виде z = f(x, y), z = z(x, y),
z = F(x, y) и т.д. Например, объем цилиндра V = pR2Н есть функция от радиуса R его основания и от высоты Н, т.е. V = f(R, Н), которая дает возможность, зная значения независимых переменных R и Н, установить соответствующее значение для V.
В экономических исследованиях часто используется производственная функция Кобба-Дугласа  , где z - величина общественного продукта, x - затраты труда, y - объем производственных фондов (обычно z и y измеряются в стоимостных единицах, x - в человеко-часах); A, a, b - постоянные. Функция Кобба-Дугласа является функцией двух независимых переменных: z = f(x, y). Частное значение функции z = f(x, y) при x = xo, y=yo обозначается zo= f(xo, yo). Геометрически область определения функции D представляет собой конечную или бесконечную часть плоскости, ограниченную линиями, которые могут принадлежать или не принадлежать этой области. В первом случае область D называется замкнутой и обозначается D, во втором случае - открытой. Наподобие того, как функция y = f(x) геометрически иллюстрируется своим графиком, можно геометрически истолковать и уравнение z = f(x, y). Возьмем в пространстве R 3 прямоугольную систему координат и изобразим на плоскости Oxy область D. В каждой точке M(x, y)ÎD восстановим перпендикуляр к плоскости Oxy и отложим на нем значение z = f(x, y). Геометрическое место полученных таким образом точек и явится своего рода пространственным графиком нашей функции. Это будет, вообще говоря, некоторая поверхность, поэтому уравнение z = f(x, y) называется уравнением поверхности. Пара значений x и y определяет на плоскости Oxy точку M(x, y), а z = f(x, y) - аппликату соответствующей точки P(x, y, z) на поверхности. Поэтому говорят, что z есть функция точки M(x, y) и пишут z = f(M).
, где z - величина общественного продукта, x - затраты труда, y - объем производственных фондов (обычно z и y измеряются в стоимостных единицах, x - в человеко-часах); A, a, b - постоянные. Функция Кобба-Дугласа является функцией двух независимых переменных: z = f(x, y). Частное значение функции z = f(x, y) при x = xo, y=yo обозначается zo= f(xo, yo). Геометрически область определения функции D представляет собой конечную или бесконечную часть плоскости, ограниченную линиями, которые могут принадлежать или не принадлежать этой области. В первом случае область D называется замкнутой и обозначается D, во втором случае - открытой. Наподобие того, как функция y = f(x) геометрически иллюстрируется своим графиком, можно геометрически истолковать и уравнение z = f(x, y). Возьмем в пространстве R 3 прямоугольную систему координат и изобразим на плоскости Oxy область D. В каждой точке M(x, y)ÎD восстановим перпендикуляр к плоскости Oxy и отложим на нем значение z = f(x, y). Геометрическое место полученных таким образом точек и явится своего рода пространственным графиком нашей функции. Это будет, вообще говоря, некоторая поверхность, поэтому уравнение z = f(x, y) называется уравнением поверхности. Пара значений x и y определяет на плоскости Oxy точку M(x, y), а z = f(x, y) - аппликату соответствующей точки P(x, y, z) на поверхности. Поэтому говорят, что z есть функция точки M(x, y) и пишут z = f(M).
|
|
|
Функция f(M) имеет предел A,  , если разность f(M) - A есть бесконечно малая, когда r = MoM ® 0 при любом способе приближения M к Mo (например, по любой линии).
, если разность f(M) - A есть бесконечно малая, когда r = MoM ® 0 при любом способе приближения M к Mo (например, по любой линии).
Функция f(x, y) называется непрерывной в точке Mo, если 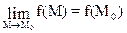 .
.
В экономике рассматриваются функции не только от двух, но и большего числа независимых переменных. Например, уровень рентабельности R зависит от прибыли П на реализованную продукцию, величин основных (a) и оборотных (b) фондов, R = П/(a+b), т.е. R является функцией трех независимых переменных R = f(П, a, b). Областью определения функции трех переменных является множество точек пространства R 3, но непосредственной геометрической интерпретации для функций с числом аргументов больше двух не существует, однако для них вводятся по аналогии все определения (частные производные, предел, непрерывность и т.д.), сформулированнные для f(x,y).
Аналогично определяется функция n независимых переменных
z = f(x1, x2,..., xn).
Областью определения такой функции будет множество D Ì R n. Примером функций многих переменных в экономике являются производственные функции. При рассмотрении любого производственного комплекса как открытой системы (входами которой служат затраты ресурсов - людских и материальных, а выходами - продукция) производственная функция выражает устойчивое количественное соотношение между входами и выходами. Производственная функция обычно задается уравнением z = f(x1, x2,..., xn), где все компоненты выпуска объединены (по стоимости или в натуре) в одну скалярную величину z, а разнородные производственные ресурсы обозначены как xi .
|
|
|
Частной производной функции нескольких переменных по одной из этих переменных называется производная, взятая по этой переменной при условии, что все остальные переменные остаются постоянными. Для функции двух переменных z = f(x, y) частной производной по переменной x называется производная этой функции по x при постоянном y. Обозначается частная производная по x следующим образом: 
 .
.
Аналогично частной производной функции z = f(x, y) по аргументу y называется производная этой функции по y при постоянном x. Обозначения:
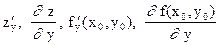 .
.
Частными производными второго порядка функции z = f(x, y) называются частные производные от ее частных производных первого порядка. Если первая производная была взята, например, по аргументу x, то вторые производные обозначаются символами  .
.
Пусть функция z = f(x, y) определена в области D и точка Mo(xo, yo) будет внутренней точкой этой области. Говорят, что функция f(x, y) в точке Mo(xo, yo) имеет максимум (минимум), если ее можно окружить такой окрестностью
(xo - d, xo + d; yo - e, yo+ e),
чтобы для всех точек этой окрестности выполнялось неравенство
f(x,y) £ f(xo,yo) (f(x,y) ³ f(xo,yo)).
Функция многих переменных может иметь максимум или минимум (экстремум) только в точках, лежащих внутри области определения функции, в которой все ее частные производные первого порядка равны нулю или не существует хотя бы одна из них. Такие точки называются критическими. Названные условия являются необходимыми условиями экстремума, но еще не достаточными (они могут выполняться и в точках, где нет экстремума). Чтобы критическая точка была точкой экстремума, должны выполняться достаточные условия. Сформулируем достаточные условия экcтремума для функции двух переменных. Пусть точка Mo(xo, yo) - критическая точка функции z = f(x, y), т.е.  , и функция
, и функция
z = f(x, y) имеет непрерывные вторые частные производные в некоторой окрестности точки Mo(xo, yo). Обозначим 
 . Тогда:
. Тогда:
1) если D > 0, то функция z имеет экстремум в точке Mo: максимум при A < 0, минимум при A > 0;
2) если D < 0, то экстремума в точке Mo нет;
3) если D = 0, то требуется дополнительное исследование.
Пример 3.28. Исследовать функцию z = y4 - 2xy2 + x2 + 2y + y2 на экстремум.
|
|
|
Решение. Находим частные производные:  = - 2y2 + 2x,
= - 2y2 + 2x, 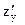 = 4y3 - 4xy +2 +2y. Для отыскания критических точек решим систему уравнений:
= 4y3 - 4xy +2 +2y. Для отыскания критических точек решим систему уравнений:  .
.
Итак, Mo(1,-1) -единственная точка, “подозрительная на экстремум”. Находим вторые частные производные:  , следовательно, A=2, B=4, С=10, D = 4, т.е. D > 0, функция имеет экстремум в точке Mo - минимум (A>0). Вычислим z min = (-1)4 - 2×1×(-1)2 +1 - 2 +1 = -1.
, следовательно, A=2, B=4, С=10, D = 4, т.е. D > 0, функция имеет экстремум в точке Mo - минимум (A>0). Вычислим z min = (-1)4 - 2×1×(-1)2 +1 - 2 +1 = -1.
В естествознании, технике и экономике часто приходится иметь дело с эмпирическими формулами, т.е. формулами, составленными на основе обработки статистических данных или результатов опытов. Одним из распространенных приемов построения таких формул является метод наименьших квадратов. Изложим идею этого способа, ограничиваясь случаями линейной и квадратичной зависимости. Пусть требуется установить зависимость между двумя величинами x и y, например, между стоимостью потребляемого сырья и стоимостью выпущенной продукции. Произведем обследование n видов продукции и представим результаты исследования в виде таблицы:
| x | x1 | x2 | ... | xn |
| y | y1 | y2 | ... | yn |
Из анализа таблицы нелегко обнаружить наличие и характер зависимости между x и y. Поэтому обратимся к графику. Допустим, что точки, взятые из таблицы (опытные точки) группируются около некоторой прямой линии. Тогда можно предположить,что между x и y существует линейная зависимость`y= ax+b, где a и b - коэффициенты, подлежащие определению,` y - теоретическое значение ординаты. Проведя прямую “на глаз”, можно графически найти b и a=tg a, однако это будут весьма неточные результаты. Для нахождения a, b применяют метод наименьших квадратов.
Перепишем уравнение искомой прямой в виде ax + b -`y=0. Точки, построенные на основе опытных данных, вообще говоря, не лежат на этой прямой. Поэтому если подставить в уравнение прямой вместо x и` y заданные величины xi и yi, то окажется, что левая часть уравнения
равна какой-то малой величине ei=`yi -yi; а именно: для первой точки
ax1 + b - y1 = e1, для второй - ax2 + b - y2 = e2, для последней -
axn + b - yn = en. Величины e1, e2,..., en, не равные нулю, называются погрешностями. Геометрически это разность между ординатой точки на прямой и ординатой опытной точки с той же абсциссой. Погрешности зависят от выбранного положения прямой, т.е. от a и b. Требуется подобрать a и b таким образом, чтобы эти погрешности были возможно меньшими по абсолютной величине. Способ наименьших квадратов состоит в том, что a и b выбираются из условия, чтобы сумма квадратов погрешностей u =  была минимальной. Если эта сумма квадратов окажется минимальной, то и сами погрешности будут в среднем малыми по абсолютной величине. Подставим в выражение для u вместо ei их значения.
была минимальной. Если эта сумма квадратов окажется минимальной, то и сами погрешности будут в среднем малыми по абсолютной величине. Подставим в выражение для u вместо ei их значения.
|
|
|
u = (ax1 + b - y1) 2 + (ax2 + b - y2) 2 +... + (axn + b - yn)2, или u = u(a,b),
где xi, yi известные величины, a и b - неизвестные, подлежащие
определению. Выберем a и b так, чтобы u(a,b) имело наименьшее
значение. Необходимые условия экстремума  ,
,  . Имеем:
. Имеем:
 = 2(ax1 + b - y1)x1 +... +2 (ax1 + b - y1)xn,
= 2(ax1 + b - y1)x1 +... +2 (ax1 + b - y1)xn,  = 2(ax1 + b - y1) +... +
= 2(ax1 + b - y1) +... +
+ 2 (ax1 + b - y1). Получаем систему:
 .
.
Эта система называется нормальной системой метода наименьших квадратов. Из нее находим a и b и затем подставляем их в эмпирическую формулу `y = ax + b. Пусть теперь точки на графике располагаются вблизи некоторой параболы так, что между x и y можно предположить квадратичную зависимость:`y=ax2 + bx + c, тогда 
 . Тогда u =
. Тогда u =  =
= 
 . Здесь u = u(a, b, c) - функция трех независимых переменных a, b, c. Необходимые условия экстремума
. Здесь u = u(a, b, c) - функция трех независимых переменных a, b, c. Необходимые условия экстремума  ,
,  ,
,  в этом случае примут следующий вид:
в этом случае примут следующий вид:
 .
.
Получили нормальные уравнения способа наименьших квадратов для квадратичной зависимости `y = ax2 + bx + c, коэффициенты которой находим, решая систему трех линейных уравнений с тремя неизвестными.
Отыскание уравнения прямой по эмпирическим данным называется выравниванием по прямой, а отыскание уравнения параболы - выравниванием по параболе. В экономических расчетах могут встретиться также и другие функции. Довольно часто встречаются эмпирические формулы, выражающие обратно пропорциональную зависимость, графически изображаемую гиперболой. Тогда говорят о выравнивании по гиперболе и т.д.
Метод наименьших квадратов оказывается весьма эффективным при исследовании качества промышленной продукции в зависимости от определяющих его факторов на основе статистических данных текущего контроля качества продукции, в задачах моделирования потребительского спроса.
Пример 3.29. Темпы роста y производительности труда по годам в промышленности республики приведены в таблице.
| x | ||||||||
| y |
Предполагая, что зависимость y от x линейная: y = ax + b, найти a и b.
Решение. Вычислим коэффициенты нормальной системы уравнений:  .
.
Следовательно, имеем систему  , решая которую, получим: a» 15,93; b» 110,57. Итак, получили уравнение искомой прямой:
, решая которую, получим: a» 15,93; b» 110,57. Итак, получили уравнение искомой прямой:
y = 15,93x + 110,57.
|
|
|
Интегралы
8.1. Основные методы интегрирования
Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x Î X справедливо равенство:
F¢ (x) = f(x). (8.1)
Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение -
ò f(x) dx.
Если F(x) - какая-нибудь первобразная для функции f(x), то
ò f(x)dx = F(x) + C, (8.2)
где С - произвольная постоянная.
Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:
1) d ò f(x)=f(x)dx,
2) ò df(x)=f(x)+C,
3) ò af(x)dx=aò f(x)dx (a=const),
4) ò(f(x)+g(x))dx= ò f(x)dx+ ò g(x)dx.
Список табличных интегралов
1. ò xm dx = xm+1/(m + 1) +C (m ¹ -1).
2.  = ln êx ê +C.
= ln êx ê +C.
3. ò ax dx = ax/ln a + C (a>0, a¹1).
4. ò ex dx = ex + C.
5. ò sin x dx = cos x + C.
6. ò cos x dx = - sin x + C.
7.  = arctg x + C.
= arctg x + C.
8.  = arcsin x + C.
= arcsin x + C.
9. 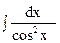 = tg x + C.
= tg x + C.
10.  = - ctg x + C.
= - ctg x + C.
Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.
Если функция f(z) непрерывна на [a, b], функция z=g(x) имеет на [a,b] непрерывную производную и a £ g(x) £b, то
ò f(g(x)) g¢ (x) dx = ò f(z) dz, (8.3)
причем после интегрирования в правой части следует сделать подстановку z=g(x).
Для доказательства достаточно записать исходный интеграл в виде:
ò f(g(x)) g¢ (x) dx = ò f(g(x)) dg(x).
Например:
1)  ;
;
2)  .
.
Пусть u = f(x) и v = g(x) - функции, имеющие непрерывные производные. Тогда, по правилу дифференцирования произведения,
d(uv)= udv + vdu или udv = d(uv) -vdu.
Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:
ò udv = uv - ò vdu. (8.4)
Эта формула выражает правило интегрирования по частям. Оно приводит интегрирование выражения udv=uv'dx к интегрированию выражения vdu=vu'dx.
Пусть, например, требуется найти ò x cosx dx. Положим u = x, dv = cos x dx, так что du=dx, v=sinx. Тогда
ò x cos x dx = ò x d(sin x) = x sin x - ò sin x dx = x sin x + cos x + C.
Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,
ò xk lnmx dx, ò xk sin bx dx, ò xk cos bx dx, ò xk e ax dx
и другие, которые вычисляются именно с помощью интегрирования по частям.
Понятие определенного интеграла вводится следующим образом. Пусть на отрезке [a, b] определена функция f(x). Разобьем отрезок [a, b] на n частей точками a = x0 < x1 <...<xn = b. Из каждого интервала (xi-1, xi) возьмем произвольную точку xi и составим сумму  f(xi)D xi, где
f(xi)D xi, где
D xi = xi - xi-1. Сумма вида  f(xi)D xi называется интегральной суммой, а ее предел при l = max D xi ®0, если он существует и конечен, называется определенным интегралом функции f(x) от a до b и обозначается:
f(xi)D xi называется интегральной суммой, а ее предел при l = max D xi ®0, если он существует и конечен, называется определенным интегралом функции f(x) от a до b и обозначается:


 f(xi)D xi. (8.5)
f(xi)D xi. (8.5)
Функция f(x) в этом случае называется интегрируемой на отрезке
[a, b],числа a и b носят название нижнего и верхнего предела интеграла.
Для определенного интеграла справедливы следующие свойства:
1) 

 ;
;
2)  ;
;
3)  -
-  ;
;
4) 
 , (k = const, kÎ R);
, (k = const, kÎ R);
5)  ;
;
6) 
 ;
;
7)  f(x)(b-a) (xÎ[a,b]).
f(x)(b-a) (xÎ[a,b]).
Последнее свойство называется теоремой о среднем значении.
Пусть f(x) непрерывна на [a, b]. Тогда на этом отрезке существует неопределенный интеграл
ò f(x) dx = F(x) + C
и имеет место формула Ньютона-Лейбница, cвязывающая определенный интеграл с неопределенным:
 F(b) - F(a). (8.6)
F(b) - F(a). (8.6)
Геометрическая интерпретация: определенный интеграл  представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y= f(x), прямыми x = a и x = b и отрезком оси Ox.
представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y= f(x), прямыми x = a и x = b и отрезком оси Ox.
Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:
 . (8.7)
. (8.7)
Если этот предел существует и конечен, то  называется сходящимся несобственным интегралом от f(x) на интервале [а,+¥), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+¥). В противном случае про интеграл
называется сходящимся несобственным интегралом от f(x) на интервале [а,+¥), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+¥). В противном случае про интеграл  говорят, что он не существует, или расходится.
говорят, что он не существует, или расходится.
Аналогично определяются несобственные интегралы на интервалах
(-¥, b] и (-¥, +¥):
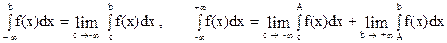 .
.
Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка [a,b], кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:
 ,
,
если эти пределы существуют и конечны. Обозначение:
 =
=  . (8.8)
. (8.8)
Пример 3.30. Вычислить ò dx/(x+2).
Решение. Обозначим t=x+2, тогда dx=dt, ò dx/(x+2) = ò dt/t = lnïtï+C =
= lnïx+2ï+C.
Пример 3.31. Найти ò tg x dx.
Решение. ò tg x dx = ò sin x/cos x dx = - ò d(cos x)/ cos x. Пусть t=cos x, тогда ò tg x dx = - ò dt/t = - lnïtï+C = - lnïcos xï+C.
Пример 3.32. Найти ò dx/sin x.
Решение.

Пример 3.33. Найти  .
.
Решение.  =
= 

Пример 3.34. Найти ò arctg x dx.
Решение. Обозначим u=arctg x, dv=dx. Тогда du = dx/(x2+1), v=x, откуда ò arctg x dx = x arctg x - ò x dx/(x2+1) = x arctg x + 1/2 ln(x2+1) +C; так как
ò x dx/(x2+1) = 1/2 ò d(x2+1)/(x2+1) = 1/2 ln(x2+1) +C.
Пример 3.35. Вычислить ò ln x dx.
Решение. Применяя формулу интегрирования по частям, получим:
u=ln x, dv=dx, du= 1/x dx, v=x. Тогда ò ln x dx = x lnx - ò x 1/x dx =
= x lnx - ò dx = x lnx - x + C.
Пример 3.36. Вычислить ò ex sin x dx.
Решение. Обозначим u = ex, dv = sin x dx, тогда du = ex dx, v=ò sin x dx= - cos x Þ ò ex sin x dx = - ex cos x + ò ex cos x dx. Интеграл ò ex cos x dx также интегрируем по частям: u = ex, dv = cos x dx Þ du=exdx, v=sin x. Имеем:
ò ex cos x dx = ex sin x - ò ex sin x dx. Получили соотношение ò ex sin x dx = - ex cos x + ex sin x - ò ex sin x dx, откуда 2 ò ex sin x dx = - ex cos x + ex sin x + С.
Пример 3.37. Вычислить J = ò cos(ln x)dx/x.
Решение. Так как dx/x = d(ln x), то J= ò cos(ln x)d(ln x). Заменяя ln x через t, приходим к табличному интегралу J = ò cos t dt = sin t + C = sin(ln x) + C.
Пример 3.38. Вычислить J =  .
.
Решение. Учитывая, что  = d(ln x), производим подстановку ln x = t. Тогда J =
= d(ln x), производим подстановку ln x = t. Тогда J =  .
.
Пример 3.39. Вычислить интеграл J =  .
.
Решение. Имеем:  . Поэтому
. Поэтому  =
=
= 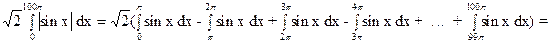
=  .
.
Пример 3.40. Можно ли применить формулу Ньютона-Лейбница к интегралу  ?
?
Решение. Нет, нельзя. Если формально вычислять этот интеграл по формуле Ньютона-Лейбница, то получим неверный результат. Действительно,  =
=  .
.
Но подынтегральная функция f(x) =  > 0 и, следовательно, интеграл не может равняться отрицательному числу. Суть дела заключается в том, что подынтегральная функция f(x) =
> 0 и, следовательно, интеграл не может равняться отрицательному числу. Суть дела заключается в том, что подынтегральная функция f(x) =  имеет бесконечный разрыв в точке x = 4, принадлежащей промежутку интегрирования. Следовательно, здесь формула Ньютона-Лейбница неприменима.
имеет бесконечный разрыв в точке x = 4, принадлежащей промежутку интегрирования. Следовательно, здесь формула Ньютона-Лейбница неприменима.
Пример 3.41. Вычислить интеграл  .
.
Решение. Подынтегральная функция определена и непрерывна при всех значениях х и, следовательно, имеет первообразную F(x)=  .
.
По определению имеем:  =
=  .
.
По формуле Ньютона-Лейбница,
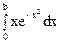 = F(b) - F(0) =
= F(b) - F(0) =  +
+  =
=  ;
;
 =
= 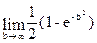 =
=  .
.
8.2.Использование интегралов в экономических расчетах
Пример 3.42. Определить объем продукции, произведенной рабочим за третий час рабочего дня, если производительность труда характеризуется функцией
f(t) = 3/(3t +1) + 4.
Решение. Если непрерывная функция f(t) характеризует производительность труда рабочего в зависимости от времени t, то объем продукции, произведенной рабочим за промежуток времени от t1 до t2 будет выражаться формулой
V =  .
.
В нашем случае
V =  = ln 10 + 12 - ln 7 - 8 = ln 10/7 + 4.
= ln 10 + 12 - ln 7 - 8 = ln 10/7 + 4.
Пример 3.43. Определить запас товаров в магазине, образуемый за три дня, если поступление товаров характеризуется функцией f(t) = 2t + 5.
Решение. Имеем:
V =  .
.
Пример 3.44. Пусть сила роста (см.6.1) описывается некоторой непрерывной функцией времени d t = f(t), тогда наращенная сумма находится как
S = P exр  d t dt,
d t dt,
а современная величина платежа P = S exр(-  d t dt).
d t dt).
Если, в чаcтности, d t является линейной функцией времени:
d t = d o + at, где d o - величина силы роста для t = 0, a - годовой прирост, то
 d t dt =
d t dt =  (d o + at)dt = d o n + an2/2;
(d o + at)dt = d o n + an2/2;
множитель наращения exр(d o n + an2/2). Если сила роста изменяется по геометрической прогрессии d t = d o at, где d o - начальное значение процентной ставки, a - годовой коэффициент роста, тогда
 d t dt =
d t dt =  d o at dt = d o at /lna
d o at dt = d o at /lna 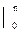 = d o(an -1)/lna;
= d o(an -1)/lna;
множитель наращения exр(d o(an -1) / lna).
Предположим, что начальный уровень силы роста равен 8%, процентная ставка ежегодно увеличивается на 20% (a=1,2), срок ссуды 5 лет. Множитель наращения в этом случае составит exр (0,08 (1,25-1) / ln1,2)»
» exр 0,653953» 1,921397.
Пример 3.45. Выше при анализе непрерывных потоков платежей предполагалось, что годовая сумма ренты R равномерно распределяется на протяжении года. На практике, особенно в инвестиционных процессах, этот поток может существенно изменяться во времени, следуя какому-либо закону. Если этот поток непрерывен и описывается некоторой функцией
R t = f (t), то общая сумма поступлений за время n равна 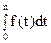 .
.
В этом случае наращенная по непрерывной ставке за период от 0 до n сумма составит:
S =  .
.
Современная величина такого потока равна
A =  .
.
Пусть функция потока платежей является линейной: Rt = Ro + at, где
Ro - начальная величина платежа, выплачиваемого за единицу времени, в которой измеряется срок ренты. Вычислим современную величину A, пользуясь правилами интегрирования определенного интеграла:
A =  =
=  +
+  .
.
Обозначим A1 =  , A2 =
, A2 =  .
.
Имеем: A1 =  = - Ro/d
= - Ro/d  ê
ê  = - Ro/d(
= - Ro/d(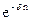 -eo) = - Ro/d(
-eo) = - Ro/d(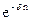 -1) =
-1) =
= Ro(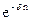 -1)/d. A2 =
-1)/d. A2 =  . Вычислим неопределенный интеграл
. Вычислим неопределенный интеграл
 по частям: u = t, dv =
по частям: u = t, dv =  dt Þ du = dt, v =
dt Þ du = dt, v =  = -
= -  /d, тогда
/d, тогда  = - t
= - t  /d + 1/d
/d + 1/d  = - t
= - t  /d (t+1/d) +C. Следовательно,
/d (t+1/d) +C. Следовательно,
A2 = -a t  /d (t+1/d)ê
/d (t+1/d)ê  = ((1-
= ((1- 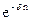 )/d - n
)/d - n 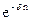 )a/d.
)a/d.
Итак, исходный интеграл
A = A1 + A2 = Ro(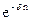 -1)/d + ((1-
-1)/d + ((1- 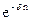 )/d - n
)/d - n 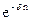 )a/d.
)a/d.
|
|
|


