 |
Порядок выполнения типового примера. 3 глава
|
|
|
|
Частные производные по параметрам в матричной форме вычисляются следующим образом:
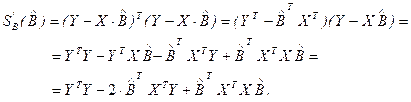
Таким образом, получим в матричной форме оценки параметров линейной регрессии:
. (2.16)
Для вычисления их не нужно составлять и решать нормальную систему линейных уравнений МНК. Достаточно выполнить указанные в формуле (2.16) алгебраические операции в матричной форме над результатами исходных, выборочных наблюдений X и Y. В частности, при выполнении контрольной работы такие расчеты достаточно легко выполняются с помощью Мастера функций табличного процессора Microsoft Exel.
3.4. Интерпретация оценок параметров и уравнения
множественной линейной регрессии
Интерпретация – содержательное объяснение – результатов анализа экономического явления или объекта, представленного статистическими (выборочными данными), является одной их самых важных задач регрессионного анализа. Так, рассматривая полученные оценки параметров уравнения регрессии, можно сказать, изменение фактора 
на одну единицу своего измерения ведет к изменению объясняемой переменной 
на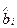 
единиц измерения этой переменной. Направление ее изменения определяется знаком коэффициента перед фактором .
При этом единицы, в которых измерены выборочные значения переменных и , влияют на величину оценок параметров регрессии 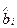. Нужно обязательно фиксировать, в каких единицах измерены значения всех переменных, прежде чем заменять слово «единица» конкретными названиями: тонны, рубли и т.п. Отсюда следует, что коэффициенты регрессии перед различными факторами нельзя сравнивать друг с другом.
Все другие более общие показатели характера влияния факторов на объясняемую переменную, не зависящие от масштаба их измерения, такие как стандартизованные коэффициенты регрессии и коэффициенты эластичности, получают на основе этих оценок параметров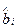 
.
|
|
|
Параметр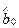 
представляет оценку значения объясняемой переменной при нулевых значениях факторных переменных. Она может иметь или не иметь экономический смысл в зависимости от характера конкретной ситуации.
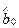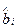При интерпретации модельного уравнения регрессии важно отмечать его следующие характерные особенности. Во-первых, и являются только оценками неизвестных констант 
и 
истинной, теоретической регрессии, которая к тому же не обязательно является линейной. Кроме того, величина и качество статистических оценок зависят от правильности выбора самого метода оценивания. В частности предпосылки МНК обосновывают условия, в которых можно получить «лучшие» оценки параметров модельной регрессии.
Во-вторых, эмпирическое уравнение регрессии отражает общую закономерную тенденцию, представленную выборочными данными, тогда как каждое отдельное наблюдение подвержено случайным воздействиям со стороны неконтролируемых факторов. Следовательно расчетные значения объясняемой переменной не могут быть детерминированными и их нужно дополнять характеристиками вариации, например, стандартными ошибками или доверительными интервалами.
И, наконец, в-третьих, правильность интерпретации зависит от правильного выбора и полноты модельного представления статистической связи. Это связано с включением в уравнение всех статистически значимых объясняющих переменных, а также выбором формы уравнения эмпирической функции регрессии. Если форма уравнения является линейной, то можно использовать такие характеристики линейной статистической связи, такие как коэффициенты парной, частной и множественной корреляции. Но в случае, когда реальная функция регрессии нелинейная, они не могут отражать силы влияния факторов.
|
|
|
4. Анализ качества уравнения регрессии
Выявление лучшего варианта эконометрической модели обычно осуществляется сравнением соответствующих им качественных характеристик, которые можно рассчитать на основе исходной статистической информации, содержащейся в векторе Y, матрице X, и новой расчетной информации, появляющейся после построении каждого из вариантов модели. Основным условием высокого «качества» модели является обоснованность математической формы уравнения эмпирической регрессии. Важную роль при этом играет как состав включенных в него независимых переменных, так и характер их взаимосвязей с зависимой переменной у, которые в совокупности определяют причины ее изменчивости.
Сопоставление новой расчетной информации, полученной после оценки параметров модельной регрессии с исходной статистической информацией позволяет установить, насколько удалось реализовать это условие на практике.
4.1. Характеристики и критерии качества эконометрических
моделей
Ведущая роль при определении характеристик качества эконометрической модели принадлежит ряду ее «выборочной» ошибки еi, i =1, 2,..., n, которая формируется с использованием найденных оценок ее параметров как
,
где 
— расчетное значение переменной уi при известных значениях независимых переменных Xj ‑ xij, i = l, 2,..., n; j = 0, 1, 2,..., p. Так для линейной модели (2.7) значения определяются на основании следующего выражения:
Для каждого набора оценок параметров 
того или иного варианта модели, описывающей рассматриваемый процесс, рассчитывается «свой» ряд ошибки ei, который можно интерпретировать как ряд оценок ее истинных, но неизвестных значений e, теоретической регрессии (2.4).
В общем случае «качество» эконометрической модели оценивается с помощью различных характеристик. Самой простой из них является средняя ошибка аппроксимации, которая вычисляется как среднее отклонение расчетных значений от результатов фактических измерений. Совокупность отклонений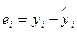 
можно рассматривать как абсолютные ошибки аппроксимации, а их абсолютные относительные величины
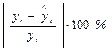
как относительные ошибки аппроксимации.
Чтобы получить общее представление о качестве модели, из относительных отклонений по каждому наблюдению вычисляют среднюю ошибку аппроксимации 
как простую среднюю арифметическую:
|
|
|
(3.1)
Считается, что допустимый предел ошибки не должен превышать 8 – 10%.
Другой характеристикой качества модельного уравнения регрессии является несмещенная оценка дисперсии случайных отклонений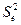 
:
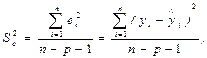(3.2)
где р – число объясняющих переменных, факторов. Корень квадратный из оценки дисперсии обозначается как Se и называется стандартной ошибкой регрессии.
Ошибка модельной регрессии во многом предопределена тем, что оценки 
рассчитывают по данным случайных измерений, и они являются случайными значениями величин b 0, b 1,, b Р ‑ неизвестных коэффициентов регрессии. Насколько хорошим оказывается соответствие между ними, насколько приемлемым можно считать «качество» полученной модели регрессии.
Надежность случайных оценок устанавливают также с помощью определения оценок их дисперсий (стандартных ошибок). Кроме того, строят доверительные интервалы для теоретических значений и проверяют статистические гипотезы о значимости отличия их эмпирических величин от ожидаемых, теоретических значений.
4.2. Дисперсии и стандартные ошибки параметров линейной регрессии
Оценки коэффициентов множественной линейной регрессии в матричной форме (2.2) определяются следующим образом:
.
Чтобы оценить ошибку оценки матрицы коэффициентов регрессии 
подставим в правую часть формулы теоретические значения объясняемой переменной 
:
Таким образом, ошибка полученной оценки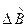 
имеет вид:
Дисперсия многомерной случайной величины 
определяется с помощью ковариационной матрицы 
:
В силу того, что объясняющие переменные XJ не являются случайными величинами, их можно вынести за знак математического ожидания:
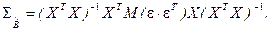(3.4)
Матрица 
представляет собой ковариационную матрицу неизвестных случайных отклонений e теоретической регрессии:
.
В силу предпосылки МНК 2° все диагональные элементы одинаковы 
, а все остальные равны нулю в силу предпосылки 3°. Таким образом, ковариационная матрица случайных ошибок 
= 
, а выражение (3.4) принимает следующий вид:
|
|
|
(3.5)
Неизвестное значение дисперсии случайного отклонения теоретической регрессии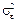 
заменяется соответствующей несмещенной выборочной оценкой 
(3.2). Следовательно, по выборке мы можем определить только выборочные оценки дисперсий коэффициентов эмпирической регрессии , которые являются диагональными элементами матрицы :
, (3.6)
где через 
обозначены диагональные элементы обратной матрицы 
, j = 0, 1, 2,..., p.
Стандартные ошибки коэффициентов регрессии вычисляются по формулам:
, (3.7)
где j = 0, 1,..., p.
4.3. Доверительные интервалы коэффициентов регрессии
Для построения интервальной оценки неизвестных коэффициентов регрессии 
вводится случайная величина 
- стандартизованный коэффициент регрессии, имеющая распределение Стьюдента с числом степеней свободы 
.
При заданном уровне значимости a доверительный интервал записывается следующим образом:
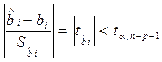
где 
- табличное значение t -критерия Стьюдента
Из данного неравенства следует:
(3.8)
где 
и 
- стандартная и предельная ошибки выборочных оценок 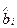соответственно.
4.4. Стандартная ошибка и доверительные интервалы уравнения регрессии
Дисперсия многомерной случайной величины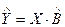 
определяется с помощью ковариационной матрицы 
:
где матрица определена формулой (3.6).
Таким образом, получаем окончательное выражение в матричной форме:
(3.9)
Выборочные оценки дисперсий i -го значения эмпирической регрессии 
, соответствующего i -му набору значений факторов (1, хi1, xi2, …, xip) в i- ой строке матрицы Х исходных данных, располагаются по диагонали матрицы 
:
. (3.10)
Стандартные ошибки оценок значений регрессии вычисляются по формулам:
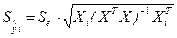, (3.11)
где i = 1, 2,..., n.
Доверительные интервалы для неизвестной функции регрессии 
строятся также с помощью случайной величины 
- стандартизованная переменная, имеющей распределение Стьюдента с числом степеней свободы , i - номер измерения.
Из данного неравенства следует:
, (3.12)
где 
и 
- стандартная и предельная ошибки расчетного значения 
соответственно.
4.5. Статистическая значимость уравнения регрессии
Проверить статистическую значимость уравнения множественной регрессии означает установить, соответствует ли регрессионная модель, принятая для объяснения взаимосвязи между переменными, исходным статистическим данным. Или, другими словами, достаточно ли включенных в уравнение регрессии факторов для описания поведения объясняемой переменной на основе имеющихся выборочных данных.
Проверка значимости уравнения регрессии производится с помощью метода статистического анализа – дисперсионного анализа. Оценивание качества уравнения регрессии с помощью F -критерия Фишера состоит в проверке гипотезы H0 о статистической значимости уравнения регрессии или показателя тесноты связи. В случае, когда нулевая гипотеза отвергается, влияние включенных в регрессию факторов на объясняемую переменную преобладает над ее изменениями в силу других причин.
|
|
|
Для этого сравнивают фактическое значение критерия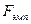 
с критическим, табличным значением 
.
,
где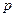 
- число объясняющих переменных, или факторов, включенных в модель.
,
где a - уровень значимости; 
и 
- число степеней свободы большей (числителя) и меньшей (знаменателя) дисперсий соответственно.
Если 
, то гипотеза H0 о случайной природе статистической связи отклоняется. С вероятностью (1- a) делается заключение о статистической значимости уравнения регрессии в целом и показателя тесноты связи 
, которые сформировались под совместным воздействием факторов Х1 и Х2, которое нет оснований считать случайным. В противном случае оснований для отклонения гипотезы H0 нет и данная статистическая связь статистически незначима.
5. Уравнение регрессии в стандартизованной форме
5.1. Стандартизованные переменные
В эконометрике часто используется иной подход к определению параметров множественной регрессии (2.13) с исключенным коэффициентом :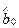
Разделим обе части уравнения на стандартное отклонение объясняемой переменной SY и представим его в виде:
Разделим и умножим каждое слагаемое на стандартное отклонение соответствующей факторной переменной, чтобы перейти к стандартизованным (центрированным и нормированным) переменным:
где новые переменные обозначены как
.
Все стандартизованные переменные имеют нулевую среднюю величину и одинаковую дисперсию, равную единице.
Уравнение регрессии в стандартизованной форме имеет вид:
, (3.1)
где 
- стандартизованные коэффициенты регрессии.
Стандартизованные коэффициенты регрессии 
отличаются от коэффициентов 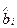обычной, естественной формы тем, что их величина не зависит масштаба измерения объясняемой и объясняющих переменных модели. Кроме того, между ними существует простая взаимосвязь:
, (3.2)
которая дает другой способ вычисления коэффициентов 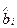по известным значениям , более удобный в случае, например, двухфакторной регрессионной модели.
5.2. Нормальная система уравнений МНК в стандартизованных
переменных
Оказывается, что для вычисления коэффициентов стандартизованной регрессии нужно знать только парные коэффициенты линейной корреляции. Чтобы показать каким образом это делается, исключим из нормальной системы уравнений МНК неизвестную 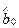с помощью первого уравнения. Умножая первое уравнение на (
) и складывая его почленно со вторым уравнением, получим:
Заменяя обозначениями дисперсии и ковариаций выражения в скобках
перепишем второе уравнение в удобном для дальнейшего упрощения виде:
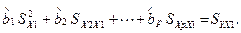
Разделим обе части этого уравнения на стандартное отклонение переменных SY и `SX1, а каждое слагаемое разделим и умножим на стандартное отклонение переменной, соответствующей номеру слагаемого:
Вводя характеристики линейной статистической связи:
,
и стандартизованные коэффициенты регрессии
,
получаем:
.
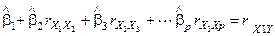После аналогичных преобразований всех остальных уравнений,нормальная система линейных уравнений МНК (2.12) принимает следующий, более простой вид:
(3.3)
5.3. Параметры стандартизованной регрессии
Стандартизованные коэффициенты регрессии в частном случае модели с двумя факторами определяются из следующей системы уравнений:
(3.4)
Решая эту систему уравнений, находим:
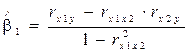, (3.5)
. (3.6)
Подставив найденные значения коэффициентов парной корреляции в уравнения (3.4) и (3.5), получим 
и 
. Затем с помощью формул (3.2) нетрудно вычислить оценки коэффициентов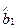 
и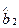 
, а затем, при необходимости, вычислить оценку 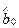по формуле 
6. Возможности экономического анализа на основе многофакторной модели
6.1. Коэффициенты 
стандартизованной регрессии
Стандартизованные коэффициенты регрессии показывают, на сколько стандартных отклонений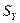 
изменится в среднем объясняемая переменная Y, если соответствующая объясняющая переменная Хi изменится на величину 
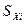одного ее стандартного отклонения при сохранении неизменным значений среднего уровня всех остальных факторов.
В силу того, что в стандартизованной регрессии все переменные заданы как центрированные и нормированные случайные величины, коэффициенты сравнимы между собой. Сравнивая их друг с другом, можно ранжировать соответствующие им факторы Хi по силе воздействия на объясняемую переменную Y. В этом состоит основное преимущество стандартизованных коэффициентов регрессии от коэффициентов регрессии в естественной форме, которые несравнимы между собой.
Эта особенность стандартизованных коэффициентов регрессии позволяет использовать при отсеве наименее значимых факторов Хi с близкими к нулю значениями их выборочных оценок 
. Решение об исключении их из модельного уравнения линейной регрессии принимается после проверки статистических гипотез о равенстве нулю его средней величины.
6.2. Средние и частные коэффициенты эластичности
В экономических исследованиях для количественного представления результатов множественного анализа также часто применяют коэффициенты эластичности. Коэффициент эластичности характеризует изменение в процентах объясняемой переменной при изменении факторной переменной на 1% и определяется для зависимости 
как
.
Он имеет четкую экономическую интерпретацию для степенной функции 
. Производная этой функции 
. Оказывается, что коэффициент эластичности при этом равен
и имеет постоянную величину.
Обобщение понятия эластичности на другие формы регрессионной связи приводит к тому, что 
оказывается зависящим от величины факторной переменной. Так для линейной регрессии 
эластичность принимает вид:
.
Поскольку коэффициент эластичности для линейной функции не является постоянной величиной, то вводят средний показатель эластичности:
.
Для характеристики относительной силы влияния каждого фактора в многофакторной регрессии используют частные коэффициенты эластичности:
В частном случае двухфакторной линейной зависимости
для характеристики влияния Х1 и Х2 на Y рассчитывают частные коэффициенты эластичности:
,
.
Экономическая интерпретация этой статистической взаимосвязи является следующей. При увеличении фактора Х1 на 1% от его среднего уровня объясняемая переменная Y изменяется на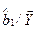 
,% своего от среднего уровня, а при увеличении фактора Х2 на 1% от его среднего уровня объясняемая переменная Y изменяется на 
,% от своего среднего уровня.
Направление изменения объясняемой переменной зависит от знака коэффициента при соответствующем факторе.
6.3. Линейные коэффициенты парной, частной и
множественной корреляции
|
|
|
