 |
Порядок выполнения типового примера. 4 глава
|
|
|
|
Наиболее обоснованной характеристикой статистической связи является выборочный коэффициент линейной корреляции. При исследовании двухфакторной модели 
линейные коэффициенты парной корреляции определяются следующим:
,
,
.
Анализируя значения коэффициентов парной корреляции, приходим к выводам относительно силы и направления взаимосвязи между каждой парой переменных. Однако очевидно, что влияние каждой из факторных переменных на объясняемую переменную не может выражаться также просто, как в случае парной регрессии, в силу их взаимосвязи между собой.
Для характеристики влияния каждого фактора множественной регрессии, аналогичной стандартизованным коэффициентам регрессии, на основе парных коэффициентов линейной корреляции рассчитывают частные коэффициенты корреляции. Они также используются при отборе факторов: целесообразность включения того или иного фактора в модель можно обосновывать величиной показателя частной корреляции.
Частные коэффициенты корреляции характеризуют влияние фактора 
на объясняемую переменную 
при устранении влияния других факторов, включенных в уравнение регрессии. В зависимости от их числа вычисляют частные корреляции различного порядка.
В случае двухфакторной модели частные коэффициенты корреляции первого порядка вычисляются непосредственно с помощью парных коэффициентов корреляции по формулам:
Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за сильной связ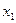и 
и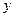 
,умеренной связ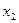и 
и 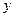коэффициенты 
и 
отличаются незначительно, 
и 
- значительно. Выводы о направлении связи на основе этих коэффициентов совпадают.
Когда общее число факторов больше двух и равно р, то возможны частные коэффициенты корреляции не только первого, но и второго, третьего, …, (р-1) порядка. Так влияние фактора 
на переменную Y можно оценить при разных способах исключения влияния других факторов: по одному, по два, …, всех (р-2) – ух факторов из числа входящих в регрессию. Хотя частная корреляция различного порядка и может представлять интерес при изучении различных взаимосвязей факторных переменных, на практике ограничиваются вычислением частных корреляций самого высокого порядка. Этими показателями обычно принято дополнять эмпирические модели множественной регрессии
|
|
|
Практическая значимость эмпирического уравнения множественной регрессии оценивается помощью коэффициента множественной корреляции 
или его квадрата 
– коэффициента множественной детерминации.
Коэффициент множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с объясняемой переменной, или оценивает тесноту совместного влияния факторов на результат. Его величина не может быть меньше, чем величина наибольшего коэффициента парной корреляции:
.
При правильном выборе факторов величина коэффициента множественной корреляции должен существенно отличаться от коэффициентов парной корреляции. Целесообразность включения в состав регрессии нового фактора можно обосновать, сравнивая коэффициенты множественной и парной корреляции с его участием.
Коэффициент множественной корреляции можно рассчитать несколькими способами, это полезно делать для контроля правильности вычислений:
1) наиболее просто это сделать для уравнения линейной регрессии в стандартизованной форме:
.
2) используя матрицу парных коэффициентов корреляции:
,
где 
- определитель матрицы коэффициентов парной корреляции;
- определитель матрицы коэффициентов парной корреляции между факторами, или межфакторного взаимодействия.
|
|
|
3) как корень квадратный из коэффициента множественной детерминации:
На основании значения коэффициента множественной регрессии делается вывод о том, что зависимостью переменной у от факторных переменных объясняется R2*100 % вариации, представленной исходными данными. Прочие факторы, не включенные в модель, составляют соответственно (1- R2)*100 % от общей вариации объясняемой переменной у.
ВАРИАНТЫ КОНТРОЛЬНЫХ ЗАДАНИЙ
Вариант 1
| X | Y | Z | X | Y | Z | X | Y | Z |
| —201 | —237 | —226 | ||||||
| —199 | —209 | —218 | ||||||
| —206 | —243 | —245 | ||||||
| —221 | —239 | —247 | ||||||
| —238 | —221 | —201 | ||||||
| —256 | —238 | —215 | ||||||
| —222 | —238 | —209 | ||||||
| —230 | —223 | —212 | ||||||
| —234 | —207 | —203 | ||||||
| —217 | —237 | —252 | ||||||
| —253 | —216 | —251 | ||||||
| —228 | —228 | —206 | ||||||
| —230 | —193 | —214 | ||||||
| —201 | —234 | —227 | ||||||
| —237 | —229 | —239 | ||||||
| —221 | —210 | —196 | ||||||
| —214 | —243 | —214 | ||||||
| —257 | —251 | —279 | ||||||
| —227 | —207 | —259 | ||||||
| —269 |
Вариант 2
| X | Y | Z | X | Y | Z | X | Y | Z |
Вариант 3
|
|
|
| X | Y | Z | X | Y | Z | X | Y | Z |
Вариант 4
| X | Y | Z | X | Y | Z | X | Y | Z |
Вариант 5
|
|
|
| X | Y | Z | X | Y | Z | X | Y | Z |
| —37 | —32 | —34 | ||||||
| —36 | —30 | —29 | ||||||
| —32 | —35 | —38 | ||||||
| —30 | —34 | —30 | ||||||
| —32 | —29 | —33 | ||||||
| —33 | —35 | —30 | ||||||
| —27 | —34 | —39 | ||||||
| —28 | —30 | —25 | ||||||
| —40 | —35 | —32 | ||||||
| —33 | —30 | —35 | ||||||
| —31 | —35 | —30 | ||||||
| —31 | —36 | —34 | ||||||
| —39 | —33 | —33 | ||||||
| —30 | —24 | —31 | ||||||
| —34 | —29 | —34 | ||||||
| —37 | —32 | —29 | ||||||
| —29 | —31 | —38 | ||||||
| —35 | —38 | —30 | ||||||
| —32 | —32 | —31 | ||||||
| —30 | —32 | —32 | ||||||
| —29 | —28 | —34 | ||||||
| —31 |
Вариант 6
| X | Y | Z | X | Y | Z | X | Y | Z |
| —262 | —256 | —273 | ||||||
| —261 | —288 | —270 | ||||||
| —268 | —269 | —266 | ||||||
| —255 | —276 | —264 | ||||||
| —261 | —266 | —270 | ||||||
| —275 | —248 | —285 | ||||||
| —263 | —281 | —268 | ||||||
| —279 | —266 | —268 | ||||||
| —269 | —282 | —272 | ||||||
| —276 | —281 | —269 | ||||||
| —274 | —265 | —273 | ||||||
| —272 | —288 | —283 | ||||||
| —284 | —290 | —269 | ||||||
| —276 | —278 | —284 | ||||||
| —275 | —282 | —270 | ||||||
| —276 | —276 | —271 | ||||||
| —250 | —271 | —271 | ||||||
| —278 | —279 | —289 | ||||||
| —267 | —273 | —294 | ||||||
| —288 | —271 | —271 | ||||||
| —266 | —264 | —271 | ||||||
| —275 | —270 | —279 | ||||||
| —285 | —261 | —277 | ||||||
| —259 | —273 | —280 | ||||||
| —264 | —283 | —263 | ||||||
| —270 | —252 | —289 | ||||||
| —281 | —283 | —278 | ||||||
| —268 | —285 | —279 | ||||||
| —277 | —279 | —265 | ||||||
| —273 | —269 | —270 | ||||||
| —262 | —268 | —264 |
Вариант 7
| X | Y | Z | X | Y | Z | X | Y | Z |
| —177 | —145 | —204 | ||||||
| —146 | —135 | —110 | ||||||
| —226 | —172 | —152 | ||||||
| —184 | —181 | —161 | ||||||
| —152 | —259 | —167 | ||||||
| —155 | —133 | —109 | ||||||
| —230 | —161 | —186 | ||||||
| —155 | —189 | —203 | ||||||
| —199 | —208 | —99 | ||||||
| —227 | —220 | —168 | ||||||
| —244 | —191 | —159 | ||||||
| —172 | —141 | —266 | ||||||
| —184 | —163 | —159 | ||||||
| —170 | —188 | —237 | ||||||
| —183 | —170 | —222 | ||||||
| —218 | —203 | —147 | ||||||
| —240 | —204 | —188 | ||||||
| —180 | —186 | —211 | ||||||
| —232 | —172 | —138 | ||||||
| —158 | —255 | —157 | ||||||
| —183 | —207 | —183 | ||||||
| —184 | —168 | —217 | ||||||
| —162 | —174 | —167 | ||||||
| —198 | —172 | —208 | ||||||
| —171 | —166 | —180 | ||||||
| —170 | —188 | —167 | ||||||
| —161 | —130 | —176 | ||||||
| —232 | —215 | —176 | ||||||
| —163 | —191 | —234 | ||||||
| —150 | —176 | —163 | ||||||
| —123 | —143 | —151 | ||||||
| —256 | —201 | —111 | ||||||
| —162 |
|
|
|
|
|
|
