Полупроводники с дырочной электропроводностью

 

Если в кристалле 4-валентного элемента часть атомов замещена атомами 3-валентного элемента (галлия Ga, ин­дия In), то для образования четырех ковалентных связей у примесного атома не хватает одного электрона (рис.

1.5, а). Этот электрон может быть получен от атома основного элемента полупроводника за счет разрыва ковалентной связи. Разрыв связи приводит к появлению дырки, так как сопровождается образованием свободного уровня в валент­ной зоне. Примеси, захватывающие электроны из валент­ной зоны, называют акцепторными или акцепторами. Энергия активизации акцепторов составляет для германия 0,0102-0,0112 эВ и для кремния 0,045-0,072 эВ, что значи­тельно меньше ширины запрещенной зоны беспримесного полупроводника. Следовательно, энергетические уров­ни примесных атомов располагаются вблизи валентной зоны (рис. 1.5, б).

Ввиду малого значения энергии активизации акцепто­ров уже при комнатной температуре электроны из валент­ной зоны переходят на уровни акцепторов. Эти электро­ны, превращая примесные атомы в отрицательные ионы, теряют способность перемещаться по кристаллической решетке, а образовавшиеся при этом дырки могут участво­вать в создании электрического тока.

За счет ионизации атомов исходного материала из валентной зоны часть электронов попадает в зону прово­димости. Однако электронов в зоне проводимости значи­тельно меньше, чем дырок в валентной зоне. Поэтому дыр­ки в таких полупроводниках являются основными, а элек­троны - неосновными

Рисунок 1.5 Условное изображение кристаллической решетки (а) и энергетическая диаграмма (б) полупроводника с дырочной электропроводностью.

подвижными носителями заряда. Такие полупроводники носят название полупроводников с дырочной электропроводностью или полупроводников р-типа. В состоянии теплового равновесия концентрация дырок в полупроводнике р-типа () и свободных элек­тронов () определяется из соотношений:

; (1.7) (1.8)

Из уравнений (1.7) и (1.8) следует, что для полупро­водника р-типа выполняется неравенство >> .

Если считать, что при комнатной температуре все акцеп­торные атомы ионизированы, т. е. =0, то на основании соотношения можно записать: 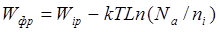, (1.9)

где N_a — концентрация акцепторных атомов в полупровод­нике.

Соотношение (1.9) показывает, что уровень Ферми в полупроводнике р-типа располагается в нижней половине запрещенной зоны, так как N_a >> n_i, и при повышении температуры смещается к середине запрещенной зоны за счет ионизации атомов основного полупроводника.

Кроме того, на основании уравнений (1.4), (1.5), (1.7) и (1.8) можно записать следующее выражение:

(1.10)

которое показывает, что введение в полупроводник приме­сей приводит к увеличению концентрации одних носите­лей заряда и пропорциональному уменьшению концентра­ции других носителей заряда за счет роста вероятности их рекомбинации.

ТОКИ В ПОЛУПРОВОДНИКАХ

 

Дрейфовый ток

 

В полупроводниках свободные электроны и дырки на­ходятся в состоянии хаотического движения. Поэтому, если выбрать произвольное сечение внутри объема полупровод­ника и подсчитать число носителей заряда, проходящих через это сечение за единицу времени слева направо и справа налево, значения этих чисел окажутся одинаковы­ми. Это означает, что электрический ток в данном объеме полупроводника отсутствует.

При помещении полупроводника в электрическое поле напряженностью Е на хаотическое движение носителей зарядов накладывается составляющая направленного дви­жения. Направленное движение носителей зарядов в элек­трическом поле обусловливает появление тока, называе­мого дрейфовым (Рисунок 1.6, а) Из-за столкновения носителей зарядов с атомами кристал- лической решетки их движение в направ­лении действия электрического поля

а)	б)
Рисунок 1.6 Дрейфовый (а) и диффузионный (б) токи в полупроводнике.

 

прерывисто и харак­теризуется подвижностью m. Подвижность равна сред­ней скорости , приобретаемой носителями заряда в направлении действия электрического поля напряженностью Е = 1 В/м, т. е.

. (1.11)

Подвижность носителей зарядов зависит от механизма их рассеивания в кристаллической решетке. Исследова­ния показывают, что подвижности электронов m_n и дырок m_p имеют различное значение (m_n > m_p) и определяются температурой и концентрацией примесей. Увеличение тем­пературы приводит к уменьшению подвижности, что зави­сит от числа столкновений носителей зарядов в единицу времени.

Плотность тока в полупроводнике, обусловленного дрей­фом свободных электронов под действием внешнего элек­трического поля со средней скоростью , определяется выражением .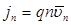

Перемещение (дрейф) дырок в валентной зоне со сред­ней скоростью создает в полупроводнике дырочный ток, плотность которого . Следовательно, полная плот­ность тока в полупроводнике содержит электронную j_n и дырочную j_р составляющие и равна их сумме (n и p — концентрации соответственно электронов и дырок).

Подставляя в выражение для плотности тока соотноше­ние для средней скорости электронов и дырок (1.11), по­лучаем

(1.12)

Если сравнить выражение (1.12) с законом Ома j =sЕ, то удельная электропроводность полупроводника опреде­ляется соотношением

.

У полупроводника с собственной электропроводностью кон­центрация электронов равна концентрации дырок (n_i = p_i), и его удельная электропроводность определяется выра­жением

.

В полупроводнике n-типа > , и его удельная электропроводность с достаточной степенью точности мо­жет быть определена выражением

.

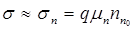В полупроводнике р-типа > , и удельная элек­тропроводность такого полупроводника

В области высоких температур концентрация электро­нов и дырок значительно возрастает за счет разрыва ковалентных связей и, несмотря на уменьшение их подвижно­сти, электропроводность полупроводника увеличивается по экспоненциальному закону.

 

Диффузионный ток

 

Кроме теплового возбуждения, приводящего к возник­новению равновесной концентрации зарядов, равномерно распределенных по объему полупроводника, обогащение полупроводника электронами до концентрации n_p и дыр­ками до концентрации p_n может осуществляться его осве­щением, облучением потоком заряжённых частиц, введе­нием их через контакт (инжекцией) и т. д. В этом случае энергия возбудителя передается непосредственно носите­лям заряда и тепловая энергия кристаллической решетки остается практически постоянной. Следовательно, избы­точные носители заряда не находятся в тепловом равнове­сии с решеткой и поэтому называются неравновесными. В отличие от равновесных они могут неравномерно распре­деляться по объему полупроводника (рисунок 1.6, б)

После прекращения действия возбудителя за счет реком­бинации электронов и дырок концентрация избыточных но­сителей быстро убывает и достигает равновесного значения.

Скорость рекомбинации неравновесных носителей про­порциональна избыточной концентрации дырок (p_n - ) или электронов (n_p - ):

; ,

где t_p - время жизни дырок; t_n - время жизни электронов. За время жизни концентрация неравновесных носите­лей уменьшается в 2,7 раза. Время жизни избыточных носителей составляет 0,01...0,001 с.

Носители зарядов рекомбинируют в объеме полупро­водника и на его поверхности. Неравномерное распределение неравновесных носите­лей зарядов сопровождается их диффузией в сторону мень­шей концентрации. Это движение носителей зарядов обу­словливает прохождение электрического тока, называемо­го диффузионным (рисунок 1.6, б).

Рассмотрим одномерный случай. Пусть в полупровод­нике концентрации электронов n(x) и дырок p(x) являют­ся функциями координаты. Это приведет к диффузионно­му движению дырок и электронов из области с большей их концентрацией в область с меньшей концентрацией.

Диффузионное движение носителей зарядов обуслов­ливает прохождение диффузионного тока электронов и дырок, плотности которых определяют­ся из соотношений:

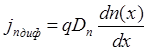; (1.13) ; (1.14)

 

где dn(x)/dx, dp(x)/dx - градиенты концентраций электронов и дырок; D_n, D_p - коэффициенты диффузии электро­нов и дырок.

Градиент концентрации характери­зует степень неравномерности распределения зарядов (электронов и дырок) в полупроводнике вдоль какого-то выбранного направления (в данном случае вдоль оси x). Коэффициенты диффузии показывают количество носителей заряда, пересекающих в единицу времени еди­ничную площадку, перпендикулярную к выбранному направ­лению, при градиенте концентрации в этом направлении, рав­ном единице. Коэффициенты

диффузии связаны с подвижностями носителей зарядов соотношениями Эйнштейна:

; .

Знак "минус" в выражении (1.14) означает противопо­ложную направленность электрических токов в полупро­воднике при диффузионном движении электронов и дырок в сторону уменьшения их концентраций.

Если в полупроводнике существует и электрическое поле, и градиент концентрации носителей, проходящий ток будет иметь дрейфовую и диффузионную составляющие. В таком случае плотности токов рассчитываются по следую­щим уравнениям:

; .

 

 

КОНТАКТНЫЕ ЯВЛЕНИЯ

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: