 |
Реальная вольтамперная характеристика p-n перехода
|
|
|
|
При выводе уравнения (1.37) не учитывались такие явления, как термогенерация носителей в запирающем слое перехода, поверхностные утечки тока, падение напряжения на сопротивлении нейтральных областей полупроводника, а также явления пробоя при определенных обратных напряжениях. Поэтому экспериментальная вольтамперная характеристика p-n перехода (кривая 2 на рис. 1.11) отличается от теоретической (кривая 1).
При обратном включении p-n перехода отличия обусловлены генерацией носителей зарядов и пробоем p-n перехода. Количество генерируемых носителей пропорционально объему запирающего слоя, который зависит от ширины p-n перехода. Поскольку ширина запирающего слоя пропорциональна 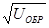 , ток генерации будет расти при увеличении обратного напряжения. Поэтому на реальной характеристике при увеличении обратного напряжения до определенного значения наблюдается небольшой рост обратного тока. Возрастанию обратного тока способствуют также токи утечки.
, ток генерации будет расти при увеличении обратного напряжения. Поэтому на реальной характеристике при увеличении обратного напряжения до определенного значения наблюдается небольшой рост обратного тока. Возрастанию обратного тока способствуют также токи утечки.
При некотором обратном напряжении наблюдается резкое возрастание обратного тока. Это явление называют пробоем p-n перехода. Существуют три вида пробоя: туннельный, лавинный и тепловой. Туннельный и лавинный пробои представляют собой разновидности электрического пробоя
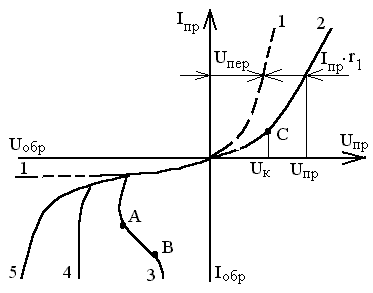
Рисунок 1.11 Отличие реальной вольтамперной характеристики p-n перехода
от теоретической.
и связаны с увеличением напряженности электрического поля в переходе. Тепловой пробой определяется перегревом перехода.
Туннельный пробой обусловлен прямым переходом электронов из валентной зоны одного полупроводника в зону проводимости другого, что становится возможным, если напряженность электрического поля в p-n переходе из кремния достигает значения 4×105 В/см, а из германия -2×105 В/см. Такая большая напряженность электрического поля возможна при высокой концентрации примесей в p- и n-областях, когда толщина p-n перехода становится весьма малой (см. формулу (1.31)). Под действием сильного электрического поля валентные электроны вырываются из связей. При этом образуются парные заряды электрон-дырка, увеличивающие обратный ток через переход. На рис. 1.10 кривая 5 представляет собой обратную ветвь вольт-амперной характеристики перехода, соответствующую туннельному пробою.
|
|
|
В широких p-n переходах, образованных полупроводниками с меньшей концентрацией примесей, вероятность туннельного просачивания электронов уменьшается и более вероятным становится лавинный пробой. Он возникает тогда, когда длина свободного пробега электрона в полупроводнике значительно меньше толщины p-n перехода. Если за время свободного пробега электроны приобретают кинетическую энергию, достаточную для ионизации атомов в p-n переходе, наступает ударная ионизация, сопровождающаяся лавинным размножением носителей зарядов. Образовавшиеся в результате ударной ионизации свободные носители зарядов увеличивают обратный ток перехода. Увеличение обратного тока характеризуется коэффициентом лавинного умножения М:
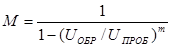 , (1.40)
, (1.40)
где UПРОБ - напряжение начала пробоя; m зависит от материала полупроводника. На рис 1.11 лавинному пробою соответствует кривая 4.
Тепловой пробой обусловлен значительным ростом количества носителей зарядов в p-n переходе за счет нарушения теплового режима. Подводимая к p-n переходу мощность Рподв = IобрUобр расходуется на его нагрев.
Выделяющаяся в запирающем слое теплота отводится преимущественно за счет теплопроводности. Отводимая от p-n перехода мощность Ротв пропорциональна разности температур перехода Tпер и окружающей среды Токр:
|
|
|
 ,
,
где Rт - тепловое сопротивление, 0К/Вт, определяющее перепад температур, необходимый для отвода 1 Вт мощности от p-n перехода в окружающую среду.
При плохих условиях отвода теплоты от перехода возможен его разогрев до температуры, при которой происходит тепловая ионизация атомов. Образующиеся при этом носители заряда увеличивают обратный ток, что приводит к дальнейшему разогреву перехода. В результате такого нарастающего процесса p-n переход недопустимо разогревается и возникает тепловой пробой, характеризующийся разрушением кристалла (кривая 3).
Увеличение числа носителей зарядов при нагреве p-n перехода приводит к уменьшению его сопротивления и выделяемого на нем напряжения. Вследствие этого на обратной ветви вольтамперной характеристики при тепловом пробое появляется участок с отрицательным дифференциальным сопротивлением (участок АВ на рис. 1.11).
Отличия реальной характеристики от теоретической на прямой ветви, в основном, обусловлены распределенным (объёмным) сопротивлением электронной и дырочной областей r1 за пределами запирающего слоя (рисунок 1.12).
Если сопротивление запирающего слоя обозначить rд, то кристалл полупроводника с запирающим слоем можно представить в виде последовательного соединения резисторов rд и r1.
При прохождении тока IПР на сопротивлении r1 падает часть напряжения внешнего источника и на запирающем слое действует напряжение UПЕР = UПР – IПР×r1. Уравнение вольтамперной характеристики в этом случае может быть записано в следующем неявном виде:
 .
.
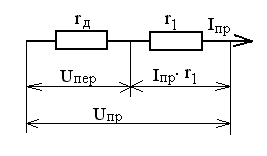
Рисунок 1.12 Упрощенная эквивалентная схема p-n перехода с распределенным сопротивлением полупроводника.
Поскольку UПЕР < UПР реальная характеристика идет ниже теоретической. Когда напряжение на запирающем слое становится равным контактной разности потенциалов, запирающий слой исчезает, и дальнейшее увеличение тока ограничивается распределенным сопротивлением полупроводников p- и n-типа. Таким образом, в точке С при UПР = UК вольтамперная характеристика переходит в прямую линию.
Емкости p-n перехода
Изменение внешнего напряжения dU на p-n переходе приводит к изменению накопленного в нем заряда dQ. Поэтому p-n переход ведет себя подобно конденсатору, емкость которого С = dQ/ dU.
|
|
|
В зависимости от физической природы изменяющегося заряда различают емкости барьерную (зарядную) и диффузионную.
Барьерная (зарядная) емкость определяется изменением нескомпенсированного заряда ионов при изменении ширины запирающего слоя под воздействием внешнего обратного напряжения. Поэтому идеальный электронно-дырочный переход можно рассматривать как плоский конденсатор, емкость которого определяется соотношением
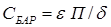 , (1.41)
, (1.41)
где П, d - соответственно площадь и толщина p-n перехода.
Из соотношений (1.41) и (1.31) следует
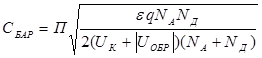 .
.
В общем случае зависимость зарядной емкости от приложенного к p-n переходу обратного напряжения выражается формулой
 ,
,
где C0 — емкость p-n перехода при UОБР = 0; g - коэффициент, зависящий от типа p-n перехода (для резких p-n переходов g = 1/2, а для плавных g = 1/3).
Барьерная емкость увеличивается с ростом NА и NД, а также с уменьшением обратного напряжения. Характер зависимости СБАР = f(UОБР) показан на рис. 1.13,а.
Рассмотрим диффузионную емкость. При увеличении внешнего напряжения, приложенного к p-n переходу в прямом направлении, растет концентрация инжектированных носителей вблизи границ перехода, что приводит к изменению количества заряда, обусловленного неосновными носителями в p- и n-областях. Это можно рассматривать как проявление некоторой емкости. Поскольку она зависит от изменения диффузионной составляющей тока, ее называют диффузионной. Диффузионная емкость представляет собой отношение приращения инжекционного заряда dQинж к вызвавшему его изменению напряжения dUпр, т. е. 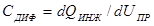 . Воспользовавшись уравнением (1.30), можно определить заряд инжектированных носителей, например дырок в n-области:
. Воспользовавшись уравнением (1.30), можно определить заряд инжектированных носителей, например дырок в n-области:
.
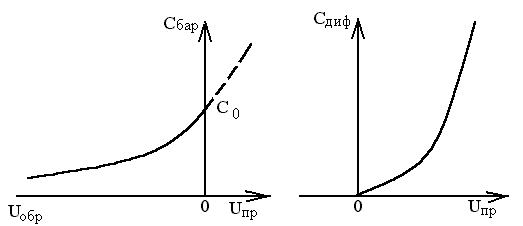
| а) | б) |
Рисунок 1.13 Зависимость барьерной (а) и диффузионной (б) емкостей p-n перехода от напряжения.
 .
.
Тогда диффузионная емкость, обусловленная изменением общего заряда неравновесных дырок в n-области, определится по формуле
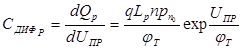 .
.
Аналогично для диффузионной емкости, обусловленной инжекцией электронов в p-область,
|
|
|
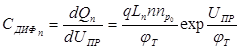 .
.
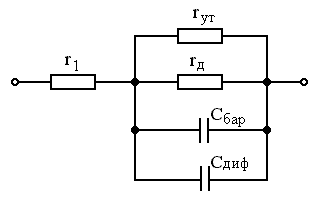
Рисунок 1.13 Эквивалентная схема p-n перехода.
Общая диффузионная емкость
 .
.
Зависимость ёмкости от прямого напряжения на p-n переходе показана на рисунке 1.13, б.
Полная емкость p-n перехода определяется суммой зарядной и диффузионной емкостей:
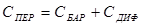 .
.
При включении p-n перехода в прямом направлении преобладает диффузионная емкость, а при включении в обратном направлении - зарядная.
На рис. 1.14 приведена эквивалентная схема p-n перехода по переменному току. Схема содержит дифференциальное сопротивление p-n перехода rД, диффузионную емкость СДИФ, барьерную емкость СБАР и сопротивление объема p- и n-областей r1. На основании уравнения (1.37) можно записать:
 .
.
Если при прямом включении p-n перехода Uпр >> jт, то:
 ;
; 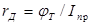 .
.
При комнатной температуре  ; (1.42)
; (1.42)
(в соотношении (1.42) значение тока подставляется в амперах). Сопротивление утечки rУТ учитывает возможность прохождения тока по поверхности кристалла из-за несовершенства его структуры. При прямом включении p-n перехода СБАР << СДИФ, дифференциальное сопротивление rД ПР мало и соизмеримо с r1, поэтому эквивалентная схема принимает вид, показанный на рис. 1.15, а.

| а) | б) |
Рисунок 1.15 Упрощенные эквивалентные схемы p-n перехода.
При обратном смещении rД ОБР >> r1, СБАР >> СДИФ и эквивалентная схема имеет вид, показанный на рис. 1.15, б.
|
|
|


