 |
Решение типовых электротехнических задач.
|
|
|
|
Типовые электротехнические задачи – это задачи, решение которых связаны с анализом и исследованием электромагнитных явлений в электротехнических устройствах. В электротехнике для описания процессов в таких устройствах пользуются методами теории электромагнитного поля и упрощенными методами, так называемыми методами теории цепей.
В теории электромагнитного поля оперируют с векторными величинами, такими как плотности токов, напряженности электрического и магнитного полей. Поэтому методы теории поля дают возможность описать процессы в каждой точке электромагнитного поля с помощью дифференциальных уравнений в частных производных (уравнения Максвелла) и рассмотреть разнообразные явления в любых электротехнических устройствах. Однако эти методы достаточно сложны, трудоемки и на практике позволяют решить ограниченное число задач.
Чаще всего для решения широкого круга электротехнических задач применяют методы теории цепей, основанные на замене реального устройства некоторой упрощенной моделью, например в виде схемы замещения [2].
При решении таких задач, пользуются системами топологических и компонентных уравнений, с помощью которых описывают процессы в модели электротехнического устройства. При этом можно выделить два основных направления, именно: исследования связанные с расчетом и анализом статических (установившихся) и динамических (переходных) режимов работы электротехнических устройств и систем.
В первом случае для расчета и анализа статических режимов работы электротехнических устройств с использованием первого и второго законов Кирхгофа записывают систему алгебраических топологических уравнений. В общем, такая система уравнений имеет вид:
|
|
|
(3.1)
где 
, 
– известные числа, а требуется определить 
неизвестных 
.
Во втором записанные для схемы замещения уравнения Кирхгофа обычно приводятся к линейному дифференциальному уравнению, порядок которого зависит от числа реактивных элементов и сложности схемы. Связь между токами в любой ветви схемы и действующей ЭДС устанавливается в следующем виде:
, (3.2)
где 
(k = 0, 1, 2,... n) – постоянные коэффициенты, зависящие от величины элементов цепи, i – ток в цепи, e (t) – внешняя ЭДС произвольного вида.
Известно, что решение уравнения (3.2) может быть представлено в форме суммы [2]
(3.3)
где 
–частное решение уравнения с правой частью, в качестве которого обычно принимается стационарное (вынужденное) решение, определяющее связь между i (t) и e (t) в установившемся режиме; 
–
решение однородного уравнения (правая часть равна нулю), определяющее переходной процесс в цепи.
Если 
то можно указать временной интервал по истечению, которого с момента начала действия ЭДС в цепи практически установится стационарный режим. Поскольку есть решение уравнения без правой части, то длительность переходного процесса не зависит от интенсивности и характера входного воздействия, а определяется свойствами цепи.
Возможность представления решения уравнения (3.2) в виде (3.3) опирается на основное свойство линейных цепей, выражающееся в принципе суперпозиции.
3.2.1. Расчет и анализ стационарных режимов работы .
Для расчета и анализа стационарных режимов с использованием пакета MathCAD воспользуемся схемами замещения для электрических цепей постоянного тока.
Пользовательская программа (модель для расчета стационарных режимов) в пакете MathCAD разрабатывается в соответствии с алгоритмом рис. 3.3. На рис. 3.4 приведена трехконтурная схема электрической цепи постоянного тока.
Разработка пользовательской программы для любого прикладного программного пакета, как и для MathCAD, необходимо начинать с анализа исходных данных технического задания. Техническое задание, как правило, определяет цели и задачи, которые необходимо достичь и решить при исследовании объекта, процесса, явления или системы.
|
|
|
При этом учитывая основные законы, определяющие функционирование и принцип работы исследуемого объекта, получают дополнительные данные, необходимые для решения конкретной задачи на том или ином этапе исследования.
Рис. 3.3. Блок – схема алгоритма пользовательской программы
При решении данной задачи в качестве исходных данных принимают параметры схемы рис. 3.3., а именно: значения сопротивлений 
и ЭДС 
. При этом в зависимости от поставленной задачи на этапе составления системы линейных независимых уравнений можно:
1. Составить на основании законов Кирхгофа систему уравнений для расчёта токов во всех ветвях схемы.
2. Составить систему уравнений для расчета токов во всех ветвях схемы методом контурных токов.
3. Составить систему уравнений для расчета токов во всех ветвях схемы методом узловых потенциалов.
4. Результаты расчёта токов, проведенного двумя методами свести в таблицу и сравнить их.
5. Составить баланс мощностей в исходной схеме.
6. Определить ток I1 (см. схему), используя теорему об эквивалентном генераторе.
7. Рассчитать и построить потенциальную диаграмму для любого замкнутого контура, включающего ЭДС.
Перед тем как составить систему уравнений, используя первый и второй законы Кирхгофа, надо произвольно выбрать:
· положительные направления токов в ветвях и обозначить их на схеме;
· положительные направления обхода контуров.
Для удобства направление обхода для всех контуров должно быть одинаковым, например, по часовой стрелке, а положительные направления токов, такие как показано на схеме.
Чтобы получить линейно независимые уравнения, по первому закону Кирхгофа составим уравнения, число которых равно числу узлов без единицы, в данном случае три уравнения. Остальные уравнения составляют по второму закону. Следует помнить что, составляя уравнения по второму закону, следует исключить те контуры, которые содержат источники тока.
|
|
|
Этап составления уравнений и определение направлений токов и напряжений желательно выполнить на листке бумаги. После чего воспользовавшись прикладным программным пакетом MathCAD разработать пользовательскую программу для расчета токов, напряжений и баланса мощностей, указанных в расчетно-графическом задании.
При составлении уравнений и записи их в пользовательскую программу необходимо использовать (жирный) знак равенства. В качестве примера приведен фрагмент программы для записи системы уравнения контурных токов схема рис. 3.4.
Рис. 3.4. Схема электрической цепи постоянного тока.
В этом случае представленная в пользовательской программе запись уравнений несет информационный характер. На основании этой записи составляются матрица параметров схемы и вектор столбец свободных членов. Предварительно сформировав блок исходных данных
Тогда матрицу параметров А можно записать в виде
а вектор столбец свободных членов как
Далее в соответствии с алгоритмом составления программы (модели) выбирают метод решения записанной системы уравнений. Наиболее простой метод – это методом обратной матрицы.
Тогда значения контурных токов записывают в виде:
При расчете токов в ветвях схемы электрической цепи, решение системы линейных уравнений чаще всего осуществляют с помощью блока встроенных функций Given – Find (Дано – Найти).
В качестве примера рассмотрим решение системы линейных уравнений такого вида [5]:
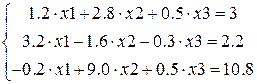(3.4)
Для этого начальные приближения искомых решений можно принять на начальном этапе поиска равными нулю:
Далее вводят ключевое слово Given (Дано);
Затем правее и ниже вводят решаемую систему уравнений в виде:
При этом следует обратить внимание на знак равенства.
Введя имя вектора–столбца результатов решения, например 
, знак присваивания и функцию поиска решения – Find с искомым аргументом в скобках, Она определяет вектор ответов – решений. Это будет выглядеть так:
Пример листинга данного фрагмента пользовательской программы представлен на рис. 3.5
|
|
|
Рис. 3.5.Решение системы линейных уравнений с применением
блока встроенных функций Given – Find.
3.2.2. Расчет характеристик эквивалентного генератора .
При анализе стационарных режимов работы ряде случаев возникает необходимость найти ток в отдельно взятой ветви электрической цепи. В этом случае нет необходимости использовать громоздкие методы расчетов определения токов во всех ветвях. В таких случаях следует использовать метод эквивалентного генератора (МЭГ). МЭГ позволяет не только рассчитать характеристики, но позволяет определить сопротивление нагрузки двухполюсника, при котором выделяется максимальная мощность, что очень важно при последовательном включении каскадов, согласованных по мощности.
Иногда этот метод называют методом холостого хода и короткого замыкания. Суть метода заключается в том, что в схеме выделяется ветвь, в которой нужно найти ток, а вся оставшаяся часть схемы заменяется активным двухполюсник – эквивалентным генератором.
Схема замещения активного двухполюсника (рис 3.6.) состоит из источника напряжения, ЭДС – 
и сопротивления 
.
Рис. 3.6. Схема замещения активного двухполюсника
Чтобы определить ЭДС генератора , следует найти напряжение холостого хода – 
относительно выходных зажимов эквивалентного генератора, это и будет искомая ЭДС. Для того чтобы найти сопротивление генератора , следует найти сопротивление относительно
выходных зажимов генератора.
При известных параметрах эквивалентного генератора тогда можно найти ток в нагрузке:
. (3.5)
Для более глубокого понимания рассмотрим пример (схема рис. 3.7).
Рис. 3.7. Схема электрической цепи
В этой схеме необходимо определить ток 
в четвёртой ветви, используя метод эквивалентного генератора.
В соответствие с поставленной задачей, прежде всего, необходимо преобразовать схему в двухполюсник. Для этого выделяем ветвь с сопротивлением 
, а всю оставшуюся часть заменяем двухполюсником –
эквивалентным генератором (рис.3.8). Затем находим напряжение холостого хода и сопротивление эквивалентного генератора.
Рис. 3.8. Преобразование схемы в двухполюсник
Чтобы найти напряжение холостого хода, необходимо найти токи во всех ветвях схемы рис. 3.9. Задав направление обхода в контурах схемы рис. 3.9 по часовой стрелке, определяют контурные токи 
и 
решив систему уравнений (3.6).
(3.6)
Рис. 3.9. Схема для определения напряжения
Анализ схемы показывает, что ток 
протекает по ветви 
и в соответствие с направлением обхода контура 
. Ток 
в ветви 
равен контурному току 
, а ток 
.
Тогда напряжение холостого хода можно определить в виде:
|
|
|
(3.7)
Для определения преобразуем схему рис. 3.9 закоротив все ЭДС, к следующему виду рис. 3.10:
Рис. 3.10. Схема для определения сопротивления эквивалентного генератора
Сопротивление определенное относительно клемм 
и 
будет внутренним сопротивлением эквивалентного генератора.
Пример листинга пользовательской программы для определения и представлен в приложение 1.
Важной характеристикой эквивалентного генератора (ЭГ) является выходная характеристика, представляющая собой зависимость выходного напряжения от тока нагрузки:
(3.8)
На рис. 3.11 приведена, рассчитанная по уравнению (3.8), характеристика ЭГ, при следующих данных. Ток нагрузки изменяется в пределах 
, а напряжение в пределах 
, 
Рис. 3.11. Выходная и нагрузочная характеристики ЭГ
Выходная характеристика позволяет определить ток нагрузки 
при любой величине нагрузочного сопротивления 
. Для того, чтобы определить ток нагрузки , достаточно умножить произвольное значение тока на величину сопротивления нагрузки 
(см. рис. 3.11), затем отложить найденное значение на графике и соединить с началом координат (на графике это сделано для нагрузки 
). Опустив перпендикуляр на ось токов с точки пересечения полученной кривой и выходной характеристики, получаем значение интересующего нас тока. В данном случае 
.
Наряду с выходной характеристикой можно выделить несколько других важных характеристик генератора – мощность нагрузки 
, в зависимости от величины сопротивления нагрузки, и мощность нагрузки 
в зависимости от величины тока нагрузки.
Определим мощность в нагрузке как функцию сопротивления нагрузки
(3.9)
Рассчитанный график данной функции по выражению (3.9) имеет следующий вид (рис. 3.12).
Определим, в каком случае выделяется максимальная мощность в нагрузке. Для этого нужно взять производную выражения по и прировнять ее нулю:
Из полученного выражения следует, что для выделения максимальной мощности необходимо выполнение условия 
.
Рис. 3.12. Зависимость мощности от нагрузочного сопротивления
Определим мощность в нагрузке как функцию тока нагрузки . После несложных преобразований получаем:
. (3.10)
Дополняя это выражение до полного квадрата, получаем:
(3.11)
Рассчитанный график данной функции по выражению (3.11) имеет следующий вид (рис. 3.13).
Рис. 3.13. Зависимость мощности от тока нагрузки
Таким образом, максимум приходится на величину тока 
равного половине тока короткого замыкания, при этом мощность равна величине
. (3.12)
Пример листинга пользовательской программы для определения зависимости приведен в приложении 2.
3.2.3. Метод комплексных амплитуд .
Ток, изменяющийся во времени называется переменным током. Ток может иметь различные формы, он может быть пилообразным, импульсным, синусоидальным. Все это переменный ток.
Традиционно в электротехнике при знакомстве со свойствами электрических цепей переменного тока и с методами их анализа используют синусоидальную форму записи гармонической функции, а в радиотехнике косинусоидальную. Обе формы записи являются равноценными и отличаются только началом отсчета значений функций.
При этом считают, что линейная электрическая цепь с сосредоточенными параметрами, находится под монохроматическом (одночастотном) гармоническом воздействии. Токи всех неуправляемых источников тока и ЭДС неуправляемых источников напряжений такой цепи есть гармонические функции времени частоты 
[12]. Где угловую частоту гармонической функции при заданной частоте 
или периоде 
определяют в виде:
(3.13)
Таким образом, задача анализа линейной электрической цепи с сосредоточенными параметрами при гармоническом воздействии сводится к решению линейного дифференциального уравнения с постоянными коэффициентами, правая часть которого является гармонической функцией времени:
. (3.14)
где 
– начальная фаза гармонической функции ЭДС.
Рассматривая установившийся режим, при котором переходные процессы в цепи полностью прекратились, решение (3.14) из теории дифференциальных уравнений имеет единственное решение
(3.15)
которое является гармонической функцией времени, с начальной фазой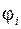 
.
Решение дифференциального уравнения (3.14) для относительно простых цепей при 
оказывается весьма трудоемким. Поэтому на практике анализ таких цепей выполняют с помощью метода комплексных амплитуд.
Метод комплексных амплитуд основан на идее функционального преобразования, когда исходные функции (оригиналы) заменяют новыми функциями (изображениями) или (символами), а именно гармоническую функцию времени представляют в виде комплексной функции времени.
, (3.16)
где 
– комплексная амплитуда.
Так как в электрических цепях переменного тока приборы, с помощью которых измеряют токи и напряжения, определяют действующие значения, то при расчете и анализе этих цепей оперируют комплексными числами.
Комплексное значение тригонометрических функций напряжения и тока в этом случае записывают в следующем виде:
(3.17)
где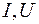 
– действующие значения тока и напряжения, 
– комплексные значения тока и напряжения.
Например, для того, чтобы сложить два тока одной частоты и разных фазовых сдвигов согласно первому закону Кирхгофа (рис.3.14)
Рис. 3.14. схема узла в цепи переменного тока
нужно проделать следующие операции, а именно:
1. представить тригонометрическую функцию (мгновенное значение) первого тока, подтекающего к узлу, в виде комплексной функции времени
;
2. представить тригонометрическую функцию (мгновенное значение) второго тока, подтекающего к узлу, в виде комплексной функции времени
3. сложить тригонометрические функции токов, используя их комплексные изображения
4. тогда значение третьего тока, оттекающего от узла можно представить в виде комплексного значения, а затем преобразовать в тригонометрическую функцию
.
Аналогично осуществляются все другие операции – умножение, деление, разность и даже дифференцирование и интегрирование:
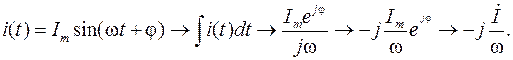
Таким образом, линейные операции над гармоническими функциями времени соответствуют операциям над их комплексными амплитудами, причем операции дифференцирования и интегрирования заменяются операциями умножения и деления. Это свойство комплексных изображений гармонических функций позволяет существенно упростить анализ линейных цепей переменного тока [12]. При этом систему интегро-дифференциальных уравнений электрического равновесия цепи можно записать ввиде системы алгебраических уравнений для комплексных изображений соответствующих токов и напряжений.
3.2.4. Расчет и анализ стационарных режимов в цепях переменного тока .
Рассмотрим и проведем анализ режима работы электрической цепи переменного тока рис. 3.15.
Рис. 3.15. Схема цепи переменного тока
Запишем второй закон Кирхгофа для замкнутого контура представленной схемы. Сумма напряжений на пассивных элементах равно величине воздействующей ЭДС.
, (3.18)
где 
– мгновенное значение ЭДС источника напряжения
Напряжения на активном, индуктивном и емкостном элементе схемы можно записать в виде:
, (3.19)
где потокосцепление 
, а заряд на емкостном элементе 
.
Учитывая компонентные выражения (3.19), отражающие физические свойства элементов схемы, топологическое уравнение (3.18) можно записать в виде:
(3.20)
Для решения этого уравнения представим его в комплексной форме:
. (3.21)
Обозначим коэффициенты пропорциональности перед токами 
через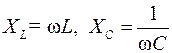 
. Данные коэффициенты, имеют размерность сопротивлений, и в электротехнике называются соответственно индуктивным и емкостным сопротивлением. Алгебраическую сумму этих сопротивлений называют полным реактивным сопротивлением 
, а 
– полным комплексным сопротивлением схемы (рис. 3.15).
Тогда уравнение (3.21) можно записать в виде:
. (3.22)
Решение данного уравнения можно представить в виде отношения комплексных чисел:
(3.23)
Уравнение (3.23) позволяет проанализировать влияние значений активного 
, индуктивного 
и емкостного 
сопротивления на стационарный режим работы цепи переменного тока, исследовать явление резонанса напряжений и изменение фазового сдвига между напряжением и током.
На (рис. 3.16) приведена зависимость действующего значения тока 
в схеме (рис. 3.15) от изменения индуктивного сопротивления .
Рис. 3.16. Зависимость тока 
.
На (рис. 3.17) приведена зависимость фазового сдвига тока 
относительно фазы ЭДС источника питания.
Анализ этих зависимостей позволяет сделать вывод о том, что при индуктивном сопротивлении 
возникает резонанс напряжений, что подтверждается максимальным значение тока (рис. 3.16). При этом анализ зависимости показывает, что в дорезонансной области при значениях Xl < Xc характер нагрузки емкостной и напряжение отстает по фазе от тока, а при Xl > Xc характер нагрузки индуктивный и напряжение опережает ток по фазе. В первом случае имеет отрицательные значения, а во втором положительные значения.
Рис. 3.17 Зависимость
|
|
|
