 |
Определение рациональных способов раскроя материала.
|
|
|
|
ОГЛАВЛЕНИЕ
Предисловие.............................................................................................................................................................................................................. 2
Глава 1. Оптимизация плана производства...................................................................................................................................................... 3
Глава 2. Оптимальное смешение....................................................................................................................................................................... 18
Глава 3. Оптимальный раскрой......................................................................................................................................................................... 31
Глава 4. Планирование финансов..................................................................................................................................................................... 40
Глава 5. Транспортная задача........................................................................................................................................................................... 53
Глава 6. Задача о назначениях.......................................................................................................................................................................... 67
Глава 7. Сетевой анализ проектов. Метод СРМ........................................................................................................................................... 78
Глава 8. Сетевой анализ проектов. Метод PERT.......................................................................................................................................... 94
Глава 9. Анализ затрат на реализацию проекта........................................................................................................................................ 105
Глава 10. Стратегические игры....................................................................................................................................................................... 132
Глава 11. Нелинейное программирование................................................................................................................................................... 147
Глава 12. Модели управления запасами...................................................................................................................................................... 166
Глава 13. Модели систем массового обслуживания................................................................................................................................. 180
|
|
|
Глава 14. Имитационное моделирование..................................................................................................................................................... 202
Глава 15. Целочисленные задачи линейного программирования......................................................................................................... 226
Глава 16. Основы теории принятия решений.............................................................................................................................................. 239
Список основной литературы.......................................................................................................................................................................... 254
Список дополнительной литературы............................................................................................................................................................ 255
Предисловие
Студент экономического вуза, прослушавший курс «Исследование операций», должен знать основные экономические проблемы, при решении которых возникает необходимость в математическом инструментарии. Он должен ориентироваться в экономической постановке задачи и определять по ней, в каком разделе исследования операций следует искать средства ее решения; должен уметь формализовать экономическую задачу, т.е. описать ее с помощью известной математической модели, провести расчеты и получить количественные результаты. Однако самое главное — студент должен уметь анализировать эти результаты и делать выводы, адекватные поставленной экономической задаче.
В каждой главе материал изложен в такой последовательности: цели, модели, примеры, вопросы, задачи, ситуации.
Цели. Устанавливаются цели изучения темы. Перечисляются основные понятия, которые должны быть изучены, и навыки, которые должны быть приобретены после изучения материала, предлагаемого в рамках данной темы.
Модели. Приводится описание экономико-математических моделей, необходимых для выполнения заданий по данной теме. Формулируются условия для применения этих моделей. Материал этого раздела можно рассматривать как краткий конспект лекции по теме.
|
|
|
Примеры. Демонстрируется, как описанные модели могут использоваться для решения экономических задач. При этом приводятся формулировка задачи, описание модели, необходимой для решения задачи, результаты расчетов по модели и анализ этих результатов.
Вопросы. Наиболее простая форма контроля знаний. Предлагается набор из нескольких вопросов и варианты ответов, один из которых верен.
Задачи. Основная форма контроля результатов обучения по программе подготовки бакалавров. Предлагается набор задач для самостоятельного решения. Решение любой задачи предполагает построение соответствующей модели, проведение необходимых расчетов и получение ответов на поставленные в задаче вопросы.
Ситуации. Основная форма контроля результатов обучения по программе подготовки магистров. Приводится описание конкретных экономических ситуаций, которые необходимо проанализировать. Цель такого анализа — научить использовать для исследования сложных экономических проблем полученные навыки решения задач. Нет и не может быть однозначных ответов на все вопросы, содержащиеся в заданиях к изложенным ситуациям. В этом принципиальное отличие ситуации от обычной задачи. Как правило, описание конкретной ситуации не содержит всей необходимой информации. Читателю приходится делать предположения и вносить необходимые добавления. Поэтому, анализируя одну и ту же ситуацию, два студента могут получить разные результаты. И оба результата будут верны. Цель анализа ситуации не сводится к получению ответа. Важен не результат, а процесс анализа.
Некоторые задачи и ситуации заимствованы из других источников и представлены в переработанном виде.
В конце каждой главы приведены ответы на вопросы и решения задач.
Данное учебное пособие можно использовать при традиционной форме проведения практических занятий, когда студенты все вместе решают задачу, предложенную преподавателем. Более современным представляется подход, основанный на использовании компьютерной технологии обучения в сочетании с программными средствами решения задач. Именно такую технологию проведения практических занятий уже более 15 лет используют авторы. В ее основе — компьютерный учебник «Исследование операций в экономике». Он содержит теоретический материал, многие из приведенных в данном учебном пособии задач, а также средства контроля правильности их решения с выборочной диагностикой ошибок.
|
|
|
Некоторые разделы исследования операций, например динамическое программирование, не представлены в этой книге, потому что авторы не могут предложить читателю удобное программное обеспечение для получения количественных оценок по соответствующим моделям.
Авторы благодарят А. Б. Ароновича за сотрудничество при подготовке глав 10 и 11, а также Н.В. Васильеву, чей опыт практических занятий по курсу «Исследование операций» позволил внести полезные коррективы в материал учебного пособия.
Глава 1. Оптимизация плана производства
Цели
В данной главе показаны возможности использования модели линейного программирования (ЛП) для определения плана производства. Эти возможности обобщаются для случая, когда закупка готовой продукции для последующей реализации может оказаться для производителя предпочтительнее, чем использование собственных мощностей. Рассматривается также задача производственного планирования, учитывающая динамику спроса, производства и хранения продукции. Наиболее часто такого рода задачи возникают на уровне агрегированного планирования и оперативного управления микроэкономическими объектами.
После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь определять и использовать для экономического анализа:
• целевую функцию;
• ограничения;
• допустимый план;
• множество допустимых планов;
• модель линейного программирования;
• оптимальный план;
• двойственные оценки;
• границы устойчивости.
Общая постановка задачи планирования производства: необходимо определить план производства одного или нескольких видов продукции, который обеспечивает наиболее рациональное использование имеющихся материальных, финансовых и других видов ресурсов. Такой план должен быть оптимальным с точки зрения выбранного критерия — максимума прибыли, минимума затрат на производство и т.д.
|
|
|
Модели
Введем обозначения:
п — количество выпускаемых продуктов;
т — количество используемых производственных ресурсов (например, производственные мощности, сырье, рабочая сила);
аij — объем затрат i- го ресурса на выпуск единицы j -й продукции;
с j — прибыль от выпуска и реализации единицы j- го продукта;
bi — количество имеющегося i -го ресурса;
хj — объем выпуска j -го продукта.
Формально задача оптимизации производственной программы может быть описана с помощью следующей модели линейного программирования:
(1)
(2)
(3)
Здесь (1) — целевая функция (максимум прибыли);
(2) — система специальных ограничений (constraint) на объем фактически имеющихся ресурсов;
(3) — система общих ограничений (на неотрицательность переменных);
хj — переменная (variable).
Задача (1)—(3) называется задачей линейного программирования в стандартной форме на максимум.
Задача линейного программирования в стандартной форме на минимум имеет вид
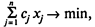(4)
(5)
(6)
Вектор х = (x 1, x 2,..., xn), компоненты хj которого удовлетворяют ограничениям (2) и (3) (или (5) и (6) в задаче на минимум), называется допустимым решением или допустимым планом задачи ЛП.
Совокупность всех допустимых планов называется множеством допустимых планов.
Допустимое решение задачи ЛП, на котором целевая функция (1) (или (3) в задаче на минимум) достигает максимального (минимального) значения, называется оптимальным решением задачи ЛП.
С каждой задачей ЛП связывают другую задачу ЛП, которая записывается по определенным правилам и называется двойственной задачей ЛП.
Двойственной к задаче ЛП (1)—(3) является задача
Соответственно, двойственной к задаче ЛП (7)—(9) является задача (1)—(3). Каждой переменной (специальному ограничению) исходной задачи соответствует специальное ограничение (переменная) двойственной задачи. Если исходная задача ЛП имеет решение, то имеет решение и двойственная к ней задача, при этом значения целевых функций для соответствующих оптимальных решений равны.
Компонента 
оптимального решения двойственной задачи (7)—(9) называется двойственной оценкой (Dual Value) ограничения 
исходной задачи ЛП.
Пусть j = max (
), где хj — компонента допустимого решения задачи (1)—(3).
Тогда при выполнении условий невырожденности оптимального решения имеют место следующие соотношения:
Изменим значение правой части bi одного основного ограничения (RHS) исходной задачи ЛП.
|
|
|
Пусть 
— минимальное значение правой части основного ограничения, при котором решение у* двойственной задачи не изменится. Тогда величину называют нижней границей (Lower Bound) устойчивости по правой части ограничения.
Пусть 
— максимальное значение правой части основного ограничения, при котором решение y* двойственной задачи не изменится. Тогда величину называют верхней границей (Upper Bound) устойчивости по правой части ограничения.
Изменим значение одного коэффициента сj целевой функции исходной задачи ЛП.
Пусть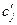 
— минимальное значение коэффициента целевой функции, при котором оптимальное решение x * исходной задачи не изменится. Тогда величину 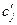называют нижней границей устойчивости по коэффициенту целевой функции.
Пусть 
— максимальное значение коэффициента целевой функции, при котором оптимальное решение х * исходной задачи не изменится. Тогда величину называют верхней границей устойчивости по коэффициенту целевой функции.
Примеры
Пример 1. Сколько производить?
Предприятие располагает ресурсами сырья и рабочей силы, необходимыми для производства двух видов продукции. Затраты ресурсов на изготовление одной тонны каждого продукта, прибыль, получаемая предприятием от реализации тонны продукта, а также запасы ресурсов указаны в следующей таблице:
Вопросы:
1. Сколько продукта 1 следует производить для того, чтобы обеспечить максимальную прибыль?
2. Сколько продукта 2 следует производить для того, чтобы обеспечить максимальную прибыль?
3. Какова максимальная прибыль?
4. На сколько возрастет максимальная прибыль, если запасы сырья увеличатся на 1 т?
5. На сколько возрастет максимальная прибыль, если допустимый объем трудозатрат увеличится с 400 до 500 ч?
Решение. Пусть х 1 — объем выпуска продукта 1 в тоннах, х 2 — объем выпуска продукта 2 в тоннах. Тогда задача может быть описана в виде следующей модели линейного программирования:
Используя пакет РОМ for WINDOWS (далее - POMWIN), исходную информацию для решения этой задачи можно представить в виде следующей таблицы:
Решая эту задачу, получаем следующий результат:
В нижней строке указан объем выпуска каждого продукта, удовлетворяющий ограничениям на ресурсы и обеспечивающий максимальную прибыль. Величина 988,24 — максимальное значение целевой функции.
Чтобы обеспечить максимальную прибыль, следует производить 16,47 т продукта 1 и 14,12 т продукта 2.
Максимальная прибыль равна 988,24 тыс. руб.
В правом столбце таблицы указаны двойственные оценки для каждого ограничения. Так, величина 3,82 показывает, что при увеличении запаса сырья на 1 т (до 121) максимальное значение целевой функции для нового оптимального плана увеличится по сравнению с 988,24 на 3,82 тыс. руб. Аналогично можно интерпретировать значение двойственной оценки 1,32 для второго ресурса.
Следующая таблица содержит дополнительную информацию, предоставляемую пакетом POMWIN:
Два правых столбца таблицы — границы устойчивости по значениям коэффициентов целевой функции (верхняя часть таблицы) и правых частей ограничений (нижняя часть).
Так, в случае если прибыль, получаемая от реализации 1 т продукта 1, изменится, но останется в пределах от 21 до 40,83, количество продукта 1 в оптимальном плане не изменится.
В случае если запас сырья изменится, но останется в пределах от 85,71 до 166,66, двойственная оценка этого ресурса не изменится.
Соответственно, если допустимый объем трудозатрат изменится в пределах от 288 до 560 ч, двойственная оценка этого ресурса не изменится.
Если допустимый объем трудозатрат увеличится с 400 до 500 ч, то максимальная прибыль увеличится на 132 тыс. руб.
Пример 2. Производить или покупать?
Фирма производит два типа химикатов. На предстоящий месяц она заключила контракт на поставку следующего количества этих химикатов:
Производство фирмы ограничено ресурсом времени работы двух химических реакторов. Каждый тип химикатов должен быть обработан сначала в реакторе 1, а затем в реакторе 2. Ниже в таблице приведен фонд рабочего времени, имеющийся у каждого реактора в следующем месяце, а также время на обработку одной тонны каждого химиката в каждом реакторе:
Из-за ограниченных возможностей, связанных с существующим фондом времени на обработку химикатов в реакторах, фирма не имеет достаточных мощностей, чтобы выполнить обязательства по контракту. Выход заключается в следующем: фирма должна купить какое-то количество этих химикатов у других производителей, чтобы использовать эти закупки для выполнения контракта. Ниже приводится таблица затрат на производство химикатов самой фирмой и на закупку их со стороны:
Цель фирмы состоит в том, чтобы обеспечить выполнение контракта с минимальными издержками. Это позволит ей максимизировать прибыль, так как цены на химикаты уже оговорены контрактом. Другими словами, фирма должна принять решение: сколько химикатов каждого типа производить у себя, а сколько — закупать со стороны для того, чтобы выполнить контракт с минимальными издержками.
Вопросы:
1. Сколько химикатов типа 1 следует производить фирме?
2. Сколько химикатов типа 2 следует производить фирме?
3. Сколько химикатов типа 1 следует закупать со стороны?
4. Сколько химикатов типа 2 следует закупать со стороны?
5. Каковы минимальные издержки на выполнение контракта?
6. Следует ли изменить объем закупок химикатов типа 2 со стороны, если их цена возрастет до 75 тыс. руб. за тонну?
7. На сколько возрастут минимальные издержки, если фонд времени работы реактора 2 сократится с 400 до 300 ч?
Решение. Введем обозначения:
x 1— количество продукта 1, производимого компанией;
z 1 — количество продукта 1, закупаемого компанией;
x 2 — количество продукта 2, производимого компанией;
z 2 — количество продукта 2, закупаемого компанией.
Модель линейного программирования приведена в следующей таблице:
Условия неотрицательности переменных: 
; 
; 
; 
.
Таблица исходной информации для расчетов в POMWIN имеет следующий вид:
Результаты расчетов:
Таблица двойственных оценок и границ устойчивости:
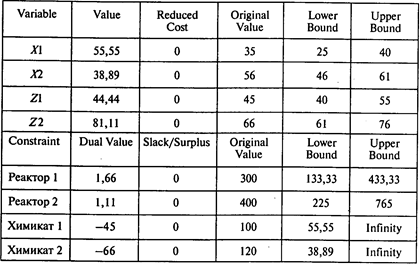
Из таблицы двойственных оценок и границ устойчивости видно, что в пределах изменения закупочной цены на химикат типа 2 от 61 до 76 (ее фактическое значение 66) оптимальный план не изменится.
Из таблицы также видно, что изменение ресурса времени работы реактора 2 в пределах от 225 до 765 не приведет к изменению двойственной оценки соответствующего ограничения.
Ответы: 1. 55,55 т. 2. 38,89 т. 3. 44,44 т. 4. 81,11 т.
5. 11 475,56 тыс. руб. 6. Нет, не следует.
7. Ha 111 тыс. руб.
Вопросы
Вопрос 1. Дана задача линейного программирования
Если эта задача имеет решение, то какие знаки имеют переменные y 1 и y 2 двойственной задачи?
Варианты ответов:
Вопрос 2. На предприятии — два цеха. Проведены оптимизационные расчеты по определению программы развития предприятия с минимальными затратами. Получены оптимальный план и двойственные оценки ограничений по загрузке мощностей двух цехов. Оказалось, что двойственная оценка ограничений на производственные мощности первого цеха равна нулю, а второго — строго положительна. Это означает, что:
1) информации для ответа недостаточно;
2) мощности обоих цехов недогружены;
3) мощности обоих цехов использованы полностью;
4) мощности цеха 1 использованы полностью, а цеха 2 недогружены;
5) мощности цеха 1 недогружены, а цеха 1 использованы полностью.
Вопрос 3. Рассматривается задача планирования нефтеперерабатывающего производства, описанная в виде модели линейного программирования. Критерий — минимум издержек. В результате решения лимитирующим фактором оказалась мощность Оборудования, измеряемая в тоннах перерабатываемой нефти. В каких единицах измеряется двойственная оценка соответствующего ограничения?
Варианты ответов:
1) т/руб.; 2) руб./ч; 3) ч/руб.; 4) руб./т; 5) т.
Вопрос 4. Рассматривается задача оптимизации плана производства нефтепродуктов. Объем производства измеряется в тоннах. Задача решается на минимум издержек. Учитывается ограничение на время использования оборудования. В каких единицах измеряется значение коэффициентов матрицы для этого ограничения?
Варианты ответов:
Вопрос 5. Рассматривается задача оптимизации производственной программы. Критерий — максимум прибыли. Оптимальное значение критерия — 100. Двойственная оценка ограничения по трудозатратам равна 0,5, по объему производства — 1,5. Чему будет равна максимальная прибыль, если общий объем трудозатрат сократится на 10 единиц?
Варианты ответов:
1) 85; 2) 90; 3) 95; 4) 100; 5) 110.
Вопрос 6. Для всякого ли многогранника существует задача линейного программирования, допустимым множеством которой он является?
Варианты ответов:
1) да, для всякого;
2) нет, только для многогранника, имеющего более трех вершин;
3) нет, только для многогранника с положительными координатами вершин;
4) нет, только для выпуклого многогранника с неотрицательными координатами вершин;
5) нет, только для выпуклого многогранника.
Вопрос 7. Допустимое решение задачи линейного программирования:
1) должно одновременно удовлетворять всем ограничениям задачи;
2) должно удовлетворять некоторым, не обязательно всем, ограничениям задачи;
3) должно быть вершиной множества допустимых решений;
4) должно обеспечивать наилучшее значение целевой функции;
5) не удовлетворяет указанным выше условиям.
Вопрос 8. Рассмотрим следующую задачу линейного программирования:
при условиях
Оптимальное значение целевой функции в этой задаче равно:
1) 1600; 2) 1520; 3) 1800; 4) 1440;
5) не равно ни одному из указанных значений.
Вопрос 9. Рассмотрим следующую задачу линейного программирования:
пои условиях
Какая из следующих точек с координатами (X, Y) не является допустимой?
Варианты ответов:
5) ни одна из указанных.
Вопрос 10. Рассмотрим следующую задачу линейного программирования:
при условиях
Множество допустимых планов имеет следующие четыре вершины: (48, 84), (0, 120), (0, 0), (90, 0). Чему равно оптимальное значение целевой функции?
Варианты ответов:
1) 1032; 2) 1200; 3) 360; 4) 1600;
5) ни одному из указанных значений.
Задачи
Задача 1. Нефтеперерабатывающая установка может работать в двух различных режимах. При работе в первом режиме из одной тонны нефти производится 300 кг темных и 600 кг светлых нефтепродуктов; при работе во втором режиме — 700 кг темных и 200 кг светлых нефтепродуктов. Ежедневно на этой установке необходимо производить 110 т темных и 70 т светлых нефтепродуктов. Это плановое задание необходимо ежедневно выполнять, расходуя минимальное количество нефти.
Вопросы:
1. Сколько тонн нефти следует ежедневно перерабатывать в первом режиме?
2. Сколько тонн нефти следует ежедневно перерабатывать во втором режиме?
3. Каков минимальный ежедневный расход нефти?
4. На сколько тонн увеличится ежедневный минимальный расход нефти, если потребуется производить в день 80 т светлых нефтепродуктов?
Задача 2. Фирма «Television» производит два вида телевизоров: «Астро» и «Космо».
В цехе 1 производят телевизионные трубки. На производство одной трубки к телевизору «Астро» требуется потратить 1,2 человекочаса, а на производство трубки к «Космо» — 1,8 человекочаса. В настоящее время в цехе 1 на производство трубок к обеим маркам телевизоров может быть затрачено не более 120 человекочасов в день.
В цехе 2 производят шасси с электронной схемой телевизора. На производство шасси для телевизора любой марки требуется затратить 1 человекочас. На производство шасси к обеим маркам телевизоров в цехе 2 может быть затрачено не более 90 человеко-часов в день.
Продажа каждого телевизора марки «Астро» обеспечивает прибыль в размере 1500 руб., а марки «Космо» — 2000 руб.
Фирма заинтересована в максимизации прибыли.
Вопросы:
1. Сколько телевизоров «Астро» следует производить ежедневно?
2. Какова максимальная ежедневная прибыль телевизионной компании?
3. На сколько рублей в день увеличится прибыль, если ресурс времени в цехе 2 возрастет на 5 человекочасов?
4. Следует ли изменить план производства, если прибыль от телевизора «Космо» увеличится до 2200 руб.?
Задача 3. Чулочно-носочная фирма производит и продает два вида товаров: мужские носки и женские чулки. Фирма получает прибыль в размере 10 руб. от производства и продажи одной пары чулок и в размере 4 руб. от производства и продажи одной пары носков.
Производство каждого изделия осуществляется на трех участках. Затраты труда (в часах) на производство одной пары указаны в следующей таблице для каждого участка:
Руководство рассчитало, что в следующем месяце фирма ежедневно будет располагать следующими ресурсами рабочего времени на каждом из участков: 60 ч на участке 1; 70 ч на участке 2 и 100 ч на участке 3.
Вопросы:
1. Сколько пар носков следует производить ежедневно, если фирма хочет максимизировать прибыль?
2. Какую максимальную прибыль фирма может получать ежедневно?
3. На сколько увеличится прибыль, если ресурс времени на участке 1 увеличится на 10ч?
4. На сколько увеличится прибыль, если ресурс времени на участке 2 увеличится на 10 ч?
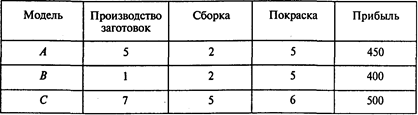
Задача 4. Василий Иванов — владелец небольшого мебельного цеха. Он производит столы трех моделей: А, В и С. Каждая модель требует определенных затрат времени на выполнение трех операций: производство заготовок, сборка и покраска.
Василий имеет возможность продать все столы, которые он изготовит. Более того, модель С может быть продана и без покраски (модель C б.п.). При этом прибыль уменьшается на 200 руб. за штуку. Василий нанимает нескольких рабочих, которые работают у него по совместительству, так что количество часов, отводимое на каждый вид работ, изменяется от месяца к месяцу.
Постройте модель линейного программирования, которая помогла бы Иванову найти такую программу выпуска продукции, чтобы прибыль в следующем месяце была максимальной. Предполагается, что по каждому виду работ возможны трудозатраты до 100 ч. В следующей таблице указаны время (в часах), необходимое для выполнения операций по производству столов каждой модели, и прибыль (в руб.), которая может быть получена от реализации каждого изделия:
Вопросы:
1. Какую максимальную прибыль может получить Василий в течение месяца?
2. Сколько столов модели А следует производить?
3. Следует ли продавать неокрашенные столы модели С?
4. На сколько увеличится максимальная прибыль, если допустимый объем трудозатрат на этапе сборки возрастет на 10%?
5. На какую минимальную величину должна возрасти прибыль от производства и продажи окрашенного стола модели С, чтобы стало выгодно их производить?
Задача 5. После предпринятой рекламной кампании фирма «Давидко» испытывает необыкновенный рост спроса на два типа мангалов для приготовления шашлыков на открытом воздухе — газовые и угольные. Фирма заключила контракт на ежемесячную поставку в магазины 300 угольных и 300 газовых мангалов.
Производство мангалов ограничивается мощностью следующих трех участков: производства деталей, сборки и упаковки. В таблице показано, сколько человекочасов затрачивается на каждом участке на каждую единицу продукции, а также приведен допустимый ежемесячный объем трудозатрат:
Фирма «Давидко» не может обеспечить выполнение контракта своими силами. Поэтому она провела переговоры с другим производителем, который в настоящее время располагает избыточными мощностями. Этот производитель согласился поставлять фирме «Давидко» в любом количестве угольные мангалы по 3 тыс. руб. за штуку и газовые мангалы по 5 тыс. руб. за штуку. Эти цены превышают себестоимость мангалов на заводе фирмы «Давидко» на 1,5 тыс. руб. за каждый угольный мангал и на 2 тыс. руб. за каждый газовый мангал. Задача фирмы «Давидко» состоит в том, чтобы найти такое соотношение закупаемых и производимых мангалов, которое обеспечило бы выполнение контракта с минимальными общими затратами.
Вопросы:
1. Каковы минимальные издержки на выполнение контракта?
2. Сколько угольных мангалов следует ежемесячно производить фирме «Давидко»?
3. Сколько газовых мангалов следует ежемесячно производить?
4. Сколько газовых мангалов следует приобретать?
5. Следует ли сохранить объемы закупок газовых мангалов, если компания, выполняющая заказы для фирмы «Давидко», поднимет цену на них до 5,5 тыс. руб.?
Задача 6. Компания «Видео», производитель видеомагнитофонов, планирует производство и запасы продукции на первое полугодие следующего года. Прогноз спроса на соответствующие шесть месяцев отражен в таблице. «Видео» хотела бы иметь такой план, который обеспечит возможность полностью удовлетворить спрос.
Из-за колебаний затрат на сырье и энергию себестоимость продукции (затраты на единицу продукции) изменяется от месяца к месяцу. Максимальный объем производства компании «Видео» также колеблется из месяца в месяц из-за неравномерного ремонта оборудования и различного числа рабочих дней в месяце.
Компания не проводит политику частого изменения числа рабочих. Поэтому, чтобы предотвратить простои, она устанавливает минимальный объем производства, составляющий 50% от максимального. В таблице представлены также максимальный и минимальный уровни запасов на каждый месяц:
На 1 января запас видеомагнитофонов отсутствует. Страховой уровень запасов, который компания старается регулярно поддерживать, составляет 2500 шт.; это означает, что и в конце каждого месяца такое количество видеомагнитофонов должно храниться на складе как минимально допустимое. Однако площади складов позволяют хранить 7000 магнитофонов. Это отражено в предпоследнем столбце таблицы.
Бухгалтерия «Видео» подсчитала, что хранение одного видеомагнитофона на складе обходится в 8 руб. в месяц. Затраты на хранение следует определять по величине запаса на конец месяца.
Определите объемы производства и запасов на каждый месяц, при которых суммарные затраты (затраты на производство плюс затраты на хранение) минимальны при условии удовлетворения спроса на продукцию без отсрочки поставок.
Вопросы:
1. Сколько магнитофонов следует произвести в феврале?
2. Каков запас на складе на конец апреля?
3. Каковы минимальные издержки на выполнение полугодового плана (в тыс. руб.)?
Ситуации
Ситуация 1. Производство обмоточной проволоки. Ярославу Алексееву понравилась его первая рабочая неделя в качестве менеджера-стажера в фирме «Электрокабель». Он еще не приобрел достаточных знаний о процессе производства, но уже получил общую информацию, побывав на заводе и встретившись со многими людьми.
Один из основных видов продукции, выпускаемой фирмой «Электрокабель», — обмоточная проволока, которая используется в производстве электрических трансформаторов. Эдуард Третьяков, менеджер, отвечающий за контроль производства, описал Алексееву стандартную процедуру обмотки. Последовательность производства проволоки такова: подготовка чертежей, протяжка, наматывание, контроль и упаковка. После технического контроля хороший товар упаковывается и отсылается на склад готовой продукции, а дефектная продукция хранится отдельно до тех пор, пока не будет отдана на переработку.
В начале марта Борис Лагутин, первый вице-президент фирмы «Электрокабель», зашел в офис Алексеева и пригласил его на собрание персонала.
«Ну что ж, давайте начнем», — сказал Лагутин, открывая собрание. «Вы уже знакомы с Ярославом Алексеевым, нашим новым менеджером-стажером. Ярослав закончил магистратуру экономического факультета МГУ, поэтому я думаю, что он сможет помочь нам решить проблему, которую мы давно обсуждаем. Я уверен, что каждый из вас будет сотрудничать с Ярославом».
Лагутин обратился к Эдуарду Третьякову с просьбой вкратце описать проблему, с которой столкнулась фирма. «Сейчас, — начал Третьяков, — мы получаем больше заказов, чем можем выполнить. Еще несколько месяцев проблему можно будет решать за счет нового оборудования, но уже в апреле нам это не поможет. В прошлом году мы сократили нескольких работников из чертежного отдела. Я собираюсь снова временно привлечь их к работе, чтобы увеличить в этом отделе объем производства. Так как мы планируем рефинансировать нашу долгосрочную задолженность по кредитам, необходимо оценить величину апрельской прибыли.
Я нахожусь в затруднительном положении, подсчитывая и оценивая, какие заказы осуществлять, а какие отложить, поэтому надо сформировать оптимальный план производства. Надеюсь, Ярослав Алексеев сможет мне помочь».
Ярослав был несколько озадачен, получив такое важное поручение в самом начале своей карьеры. Сдержав волнение, он сказал: «Дайте мне данные и день или два времени». Ему предоставили информацию в виде следующих таблиц:
Примечание: По договору с основным поставщиком фирма должна произвести в апреле 600 единиц (катушек) продукта W0007X и 150 единиц продукта W0075C.
Примечание: Объем работы по контролю качества — не проблема, так как можно работать сверхурочно, чтобы приспособиться к любому графику.
Средняя производственная выработка в месяц — 2400 ед.
Среднее использование машинного времени — 63%.
Средний процент посланной на переработку продукции — 5% (большей частью из намоточного отдела).
Задания
1. Проведите детальный анализ проблемы (с построением таблиц, графиков и использованием компьютера).
2. Ответьте на следующие вопросы:
Какие рекомендации должен дать Ярослав Алексеев и с какими обоснованиями?
Есть ли необходимость в использовании временных работников в чертежном отделе?
Следует ли расширять парк машин?
Ситуация 2. Западно-сибирская корпорация «Химикаты и удобрения».
В декабре 2002 г. Василий Маслов, генеральный директор западно-сибирского отделения корпорации «Химикаты
|
|
|
