Модель оптимального размера заказа с дефицитом.

Предположим, что:

1) темп спроса на товар известен и постоянен;

2) время выполнения заказа известно и постоянно;

3) закупочная цена не зависит от размера заказа.

Исходные данные: темп спроса, издержки заказа, издержки хра­нения, издержки дефицита.

Результат: оптимальный размер заказа, время между заказа­ми, точка восстановления запаса, совокупные издержки.

Размер заказа является постоянным. Уровень запасов убывает с постоянной интенсивностью. Допускается дефицит продукта. После получения заказа фирма компенсирует дефицит и восста­навливает запас продукта на складе. Заказ делается тогда, когда дефицит продукта на складе достигает оптимального размера. Оптимальным решением задачи будет такой размер заказа Q*, при котором минимизируются общие издержки за период, равные сум­ме издержек хранения, издержек заказа и издержек дефицита.

Динамика изменения количества продукта s на складе показа­на на рис.5.

Рис.5

Пусть Q — размер заказа;

Т — продолжительность периода планирования;

D, d — величина спроса за период планирования и в еди­ницу времени соответственно;

К — издержки одного заказа;

Н, h — удельные издержки хранения за период и в еди­ницу времени соответственно;

В, b — упущенная прибыль, возникающая вследствие дефицита одной единицы продукта, за период и в единицу времени соответственно;

S — максимальный запас продукции;

L — время выполнения заказа.

Тогда:

— издержки заказа за период планирования;

— издержки хранения за период планирования;

5. Модель оптимального размера заказа с количественными скидками.

Предположим, что:

1) темп спроса на товар известен и постоянен;

2) время выполнения заказа известно и постоянно.

Исходные данные: темп спроса, издержки заказа, издержки хра­нения, цена товара, количественные скидки в случае закупки крупных партий товара.

Результат: оптимальный размер заказа, время между заказа­ми, точка восстановления запаса, количество заказов за фиксиро­ванный период времени, совокупные издержки.

Пусть Q — размер заказа;

T — продолжительность периода планирования;

D, d —величина спроса за период планирования и в единицу времени соответственно;

К — издержки одного заказа;

Н, h — удельные издержки хранения за период и в еди­ницу времени соответственно.

Предположим, что известны числа с_i, а_i, i = 1,..., п, где с_i — цена продукта при размере заказа Q в интервале a_{i –1}£ Q < а_i. Бу­дем считать, что a ₀ = 0 и a_n = +¥.

Тогда:

Оптимальный размер заказа определяется в результате решения п задач. Каждая из этих задач сводится к определению такого раз­мера заказа Q_i, i = 1,..., п, при котором функция совокупных (об­щих) издержек достигает минимума при ограничениях

Решение исходной задачи определяется из условия

На рис. 6 изображены функции совокупных издержек для трех значений цен продукта. Значение цены c ₁ определено на интер­вале 0 £ Q < а ₁, цены с ₂ — на интервале a ₁ £ Q < а ₂, цены c ₃ — на интервале a ₂ £ Q < + ¥.

Рис. 6

Соответственно, функция общих издержек C ₁(Q) определена при значении цены с ₁ на интервале 0 £ Q < а ₁, функция C ₂(Q) — при значении цены с ₂ на интервале a ₁ £ Q < а ₂, функция C ₃(Q) — при значении цены c ₃ на интервале a ₂ £ Q < + ¥.

Минимальное значение функции C ₁(Q) в области ее допусти­мых значений достигается в точке Q ₁, функции C ₂(Q) — в точке а ₁, функции C ₃(Q) — в точке а ₂.

Оптимальный размер заказа следует выбирать из величин Q ₁, a ₁ и a ₂ по формуле

II. Стохастическая модель

6. Дискретная стохастическая модель оптимизации начально­го запаса.

Мы отказываемся от предположения о постоянстве и детерми­нированности величины спроса на товар и предполагаем извест­ным распределение величины спроса.

Пусть S — размер запаса на начало периода планирования;

D — величина спроса за период планирования (це­лое число);

Н — удельные издержки хранения за период;

В — удельные издержки дефицита за период;

p(D)— вероятность того, что величина спроса за период планирования составит D.

Функция распределения величины спроса F(x) = р (D < х) = .

В случае когда величина спроса за период планирования пре­вышает размер запаса (D > S), возникает дефицит и соответству­ющие издержки дефицита. Если запас больше, чем величина спро­са (S > D), то возникают издержки хранения. Математическое ожидание C ₁(S) величины издержек хранения за период плани­рования для размера начального запаса S можно оценить следу­ющим образом:

Математическое ожидание С ₂(S) величины издержек дефицита за период планирования для размера начального запаса S можно оценить следующим образом:

Математическое ожидание C(S) совокупных издержек в этом случае имеет вид

В стохастической модели оптимальным является такой размер начального запаса S*, при котором математическое ожидание со­вокупных издержек C(S*) имеет минимальное значение, т.е. та­кой размер запаса S*, который удовлетворяет условию

Если и оптимальными являются как размер запаса S*, так и размер запаса S * + 1.

Примеры

Пример 1. Продажа автомобилей.

Андрей Удачливый, торговый агент компании Volvo, занима­ется продажей последней модели этой марки автомобиля. Годо­вой спрос на эту модель оценивается в 4000 единиц. Цена каждо­го автомобиля равна 90 тыс. руб., а годовые издержки хранения составляют 10% от цены самого автомобиля. Анализ показал, что средние издержки заказа составляют 25 тыс. руб. на заказ. Время выполнения заказа — 8 дней. Ежедневный спрос на автомобили равен 20.

Вопросы:

1. Чему равен оптимальный размер заказа?

2. Чему равна точка восстановления?

3. Каковы совокупные издержки?

4. Каково оптимальное количество заказов в год?

5. Каково оптимальное время между двумя заказами, если предположить, что количество рабочих дней в году равно 200?

Решение. Исходные данные:

величина спроса D = 4000 единиц;

издержки заказа K = 25 тыс. руб.;

издержки хранения H = 9/200 тыс. руб.;

цена за единицу с = 90 тыс. руб.;

время выполнения заказа L = 8 дней;

ежедневный спрос d = 20 единиц;

число рабочих дней Т= 200.

Используя простейшую модель оптимального размера заказа, получаем:

размер заказа Q = 149 единиц;

точка восстановления R = 160 единиц;

число заказов за год N= 26,83;

совокупные издержки С = 1341 тыс. руб;

стоимость продаж cD = 360 млн руб.;

число дней между заказами t = 7,45.

Пример 2. Поставка товара с фиксированным интервалом времени.

Магазин «Лада» закупает духи «Ландыш» на одной из парфю­мерных фабрик. Годовой спрос на этот продукт составляет 600 шт. Издержки заказа равны 850 руб., издержки хранения — 510 руб за одну упаковку (20 шт.) в год. Магазин заключил договор на поставку с фиксированным интервалом времени.

Количество рабочих дней в году — 300. Время поставки товара — б дней. Стоимость одного флакона — 135 руб.

Вопросы:

1. Чему равно оптимальное число заказов в течение года?

2. Чему равна точка восстановления запаса?

3. Каковы минимальные совокупные издержки?

Решение. Оптимальный размер заказа

Число заказов в течение года

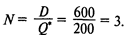
Поскольку среднесуточный спрос равен 600/300 = 2 шт., точ­ка восстановления запаса составит 2 • 6 = 12 шт. Минимальные издержки заказа и хранения

Ответы: 1.3. 2.12шт. 3.5100руб.

Пример 3. Производство деталей.

На первом станке производятся детали в количестве 12 000 еди­ниц в год. Эти детали используются для производства продукции на втором станке производительностью 3600 единиц в год. Остав­шиеся детали образуют запас. Издержки хранения составляют 0,5 руб. за одну деталь в год. Стоимость производственного цикла на первом станке равна 800 руб. Определите оптимальный размер партии на первом станке.

Решение. Оптимальный размер партии

Пример 4. Планирование дефицита.

Вернемся к примеру 2 и рассмотрим вариант планирования дефицита. Допустим, по оценке менеджера, упущенная прибыль, связанная с отсутствием товара и утратой доверия клиентов, со­ставляет 20 руб. в год за один флакон духов «Ландыш» при усло­вии, что издержки заказа и хранения остаются без изменения. Определите оптимальный размер заказа при плановом дефиците. Нужно ли менеджеру вводить систему с плановым дефицитом?

Решение. Оптимальный размер заказа

Максимальный размер запаса за один цикл

Совокупные издержки

Совокупные издержки при плановом дефиците меньше издер­жек без дефицита на 1718,7 руб. Следовательно, целесообразно ввести систему с плановым дефицитом.

Пример 5. Продажи со скидками.

Магазин «Медвежонок» продает игрушечные гоночные машин­ки. В зависимости от размера заказа фирма предлагает скидки:

Издержки заказа составляют 49 руб. Годовой спрос на машин­ки равен 5000. Годовые издержки хранения в процентном отно­шении к цене составляют 20%. Найдите размер заказа, миними­зирующий общие издержки.

Решение. Рассчитаем Q* для каждого вида скидок: Q ₁ * = 700, Q ₂ * = 714, Q ₃ * = 718.

Так как Q ₁ * находится в интервале между 0 и 1000, то его необ­ходимо взять равным 700. Оптимальный объем со скидкой Q ₂ * меньше количества, необходимого для получения скидки, следо­вательно, его необходимо принять равным 1000 единиц. Анало­гично Q ₃ * берем равным 2000 единиц.

Получим: Q ₁ * = 700, Q ₂ * = 1000, Q ₃ * = 2000.

Далее необходимо рассчитать общие издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее значе­ние. Расчеты приведены в следующей таблице:

Выберем тот размер заказа, который минимизирует общие го­довые издержки. Из таблицы видно, что заказ в размере 1000 игру­шечных машинок будет минимизировать совокупные издержки.

Пример 6. Создание запаса продукции при дискретном спросе. Небольшой салон специализируется на продаже видеомагни­тофонов стоимостью 2000 руб. Затраты на хранение единицы про­дукции составляют 500 руб. Изучение спроса, проведенное в те­чение месяца, дало следующее распределение числа покупаемых видеомагнитофонов:

Найдите оптимальный размер запаса.

Решение. Доказано, что при дискретном случайном спросе сум­марные затраты C(S) = Н (S–D)p(D) + В (D–S)p(D) минимальны при размере запаса S*, удовлетворяющем неравенству где — плотность убытков, F(S) = р (D < S) — функция распределения величины спроса. Вычислим плотность убытков:

Найдем значения функции распределения величины спроса:

Оптимальный размер запаса продукции удовлетворяет неравен­ству F (6) < 0,8 < F(7). Следовательно, размер запаса в 6 единиц будет оптимальным.

Задачи

Задача 1. Мистер Бобров приобретает в течение года 1500 те­левизоров для розничной продажи в своем магазине. Издержки хранения каждого телевизора равны 45 руб. в год. Издержки за­каза — 150 руб. Количество рабочих дней в году равно 300, время выполнения заказа — 6 дней.

Вопросы:

1. Каков оптимальный размер заказа?

2. Чему равны годовые издержки заказа?

3. Чему равна точка восстановления запаса?

Задача 2. Анна Васильева из компании «Сюрприз» продает 400 водяных кроватей в год, причем издержки хранения равны 1 тыс. руб. за кровать в день, а издержки заказа — 40 тыс. руб. Ко­личество рабочих дней равно 250, время выполнения заказа — 6 дней.

Вопросы:

1. Каков оптимальный размер заказа?

2. Чему равна точка восстановления запаса?

3. Каков оптимальный размер заказа, если издержки хранения равны 1,5 тыс. руб.?

Задача 3. Мекки Мессер владеет маленькой компанией, кото­рая выпускает электрические ножи. В среднем она может произ­водить 150 ножей в день. Дневной спрос на ножи примерно ра­вен 40 шт. Фиксированные издержки производства составляют 100 руб., издержки хранения — 8 руб. за нож в год. В году 250 ра­бочих дней.

Вопросы:

1. Каков оптимальный размер производственного заказа?

2. Чему равны издержки хранения?

3. Чему равны совокупные издержки за год?

Задача 4. Годовой заказ на тостер «Слава» для магазина Марии Монеты — 3000 единиц, или 10 единиц в день. Издержки заказа равны 25 руб., издержки хранения — 0,4 руб. в день. Так как тос­тер «Слава» очень популярен, то в случае отсутствия товара поку­патели обычно согласны подождать, пока не поступит следующая партия товара. Однако издержки вследствие дефицита равны 0,75 руб. за тостер в день.

Вопросы:

1. Сколько тостеров будет заказывать Мария?

2. Каков максимальный дефицит?

3. Чему равны совокупные издержки?

Задача 5. Магазин «Все для дома» закупает линолеум размером 2 х 3 м² в компании «Химические товары». В зависимости от раз­мера заказа компания предлагает следующие скидки:

Издержки заказа равны 45 тыс. руб. Годовые издержки хране­ния составляют 50% от закупочной цены, годовой спрос на лино­леум равен 100 кускам. Определите оптимальный размер заказа.

Задача 6. Мебельный салон «Антик» продает в год около 1000 спальных гарнитуров по цене 50 тыс. руб. Размещение одно­го заказа на поставку гарнитуров обходится в 40 тыс. руб. Годовая стоимость хранения гарнитура составляет 25% его цены. Салон может получить у поставщика скидку в 3%, если размер заказа со­ставит не менее 200 гарнитуров. Следует ли салону воспользовать­ся этой скидкой?

Вопросы

Вопрос 1. В детерминированной модели управления запасами оптимальный размер заказа:

1) прямо пропорционален величине спроса на продукт за пе­риод, обратно пропорционален удельным издержкам хранения за период и стоимости заказа;

2) прямо пропорционален величине спроса на продукт за пе­риод и стоимости заказа, обратно пропорционален удельным из­держкам хранения за период;

3) прямо пропорционален величине спроса на продукт за пе­риод и удельным издержкам хранения за период, обратно пропор­ционален стоимости заказа;

4) прямо пропорционален стоимости заказа и удельным издерж­кам хранения за период, обратно пропорционален величине спроса на продукт за период;

5) прямо пропорционален удельным издержкам хранения за пе­риод, обратно пропорционален величине спроса на продукт за период и стоимости заказа.

Вопрос 2. Для определения оптимального размера заказа в мо­дели с производством необходимо знать:

1) величину спроса, издержки заказа и темп производства;

2) издержки дефицита, величину спроса и издержки хранения;

3) издержки заказа, темп производства и упущенную прибыль;

4) время выполнения заказа, издержки дефицита и издержки заказа;

5) издержки хранения и размеры скидок.

Вопрос 3. Для определения оптимального размера заказа в мо­дели с дефицитом необходимо знать:

1) время выполнения заказа;

2) темп производства;

3) цену продукта;

4) размеры скидок;

5) издержки заказа.

Вопрос 4. Уменьшение размера заказа в модели управления за­пасами приведет к следующему результату:

1) увеличению числа упущенных продаж и увеличению затрат на хранение;

2) уменьшению числа упущенных продаж и увеличению затрат на хранение;

3) уменьшению затрат на хранение и росту издержек на оформ­ление заказов;

4) уменьшению затрат на хранение и снижению издержек на оформление заказов;

5) увеличению затрат на хранение и снижению издержек на оформление заказов.

Вопрос 5. Для определения оптимального размера заказа в мо­дели с ценовыми скидками необходимо знать:

1) величину спроса, издержки заказа и темп производства;

2) издержки дефицита, величину спроса и издержки хранения;

3) издержки заказа, величину спроса и упущенную прибыль;

4) издержки хранения, издержки заказа и цену продукта;

5) издержки хранения и размеры скидок.

Вопрос 6. Модель называется стохастической, если:

1) функции пополнения запасов и расхода — не случайные ве­личины;

2) функция пополнения запасов изменяется во времени;

3) хотя бы одна из функций пополнения запасов и расхода — случайная величина;

4) функция расхода изменяется во времени;

5) функция пополнения запасов линейно возрастает.

Ситуации

Ситуация 1. Профессиональные видеосистемы,

С тех пор как появились первые видеомагнитофоны, Владимир Алексеев начал мечтать о собственном производстве видеосистем для профессионалов. Просматривая дома свои любимые старые фильмы, Владимир планировал производство видеосистемы, по­тенциальными потребителями которой являлись бы телевизион­ные станции, рекламные агентства и другие организации, исполь­зующие технику самого высокого качества.

Базовая модель новой видеосистемы состоит из блока комплекс­ного контроля, видеодиска, двух отдельных видеомагнитофонов и профессиональной телевизионной установки. Все устройства соединены в единую систему. Кроме того, к базовой модели при­лагается усовершенствованное устройство дистанционного управ­ления. Оно управляет всей системой, посылая инфракрасные сиг­налы блоку комплексного контроля, который, в свою очередь, управляет остальными устройствами. Для предлагаемой видеоси­стемы Владимир самостоятельно разработал блок комплексного управления, который представляет собой микропроцессор, спо­собный координировать работу подсоединенных элементов сис­темы.

Базовая модель профессиональной видеосистемы обладает ря­дом преимуществ перед схожими системами. Изображение с ви­деодиска, телевизионной установки и одной из видеосистем мож­но легко переместить во вторую видеосистему. Кроме того, к блоку контроля можно подключить одну из самых распространенных моделей компьютера (Macintosh, IBM PC, Radio Shack Model 3000 и Zenith computer system), что позволяет использовать графические редакторы для создания видеопродуктов. Для улучшения качества звука имеется возможность подключения стереосистемы. Благо­даря двум видеосистемам значительно увеличиваются возможно­сти при монтаже. Розничная цена предлагаемой базовой модели профессиональной видеосистемы составляет 1950 долл.

Владимир Алексеев нашел в США производителей телевизи­онных установок, панели управления, видеодиска и заключил с ними договоры о поставках. Что касается обычных видеосистем, то они более популярны и есть возможность выбрать поставщи­ка. После тщательного исследования Владимир остановил свой выбор на двух японских компаниях: Toshiki и Копу.

Toshiki — это новая компания, она находится недалеко от То­кио. Как и другие поставщики, Toshiki предлагает скидки опто­вым покупателям:

Другим японским поставщиком может стать компания Копу. Хотя эта компания также создавалась в Японии, сегодня она имеет сеть филиалов по всему миру, один из которых расположен в России.

Копу также предлагает скидки оптовикам:

Поскольку Копу имеет производственные мощности в России, то издержки на размещение заказа и время его выполнения мень­ше, чем в компании Toshiki:

Владимир оценивает издержки хранения в 30% от закупочной цены. Эта величина учитывает хранение и уход за оборудовани­ем, а также включает потенциальные издержки от морального износа видеосистем.

В первый год Владимир начал продавать только базовую мо­дель (блок контроля, видеодиск, телевизионную установку и две видеосистемы). В течение первых шести месяцев спрос на нее был примерно постоянным. Например, в июне было продано 7970 шт., в июле — 8070, в августе — 7950, а в сентябре — 8010 шт. Предпо­лагается, что данная тенденция сохранится в течение нескольких следующих месяцев.

Задания

1. Найдите точки восстановления запаса для обеих компаний.

2. Если бы вы были на месте Владимира, то какую компанию, производящую видеосистемы, вы бы выбрали?

3. Владимир рассматривает несколько альтернативных страте­гий. Первая предполагает продажу всех составляющих по от­дельности. Вторая стратегия предусматривает модификацию блока контроля, которая позволит использовать как видео­системы, предлагаемые Алексеевым, так и другие видео­системы. Если эти стратегии будут реализованы, как это по­влияет на точки восстановления запаса?

4. Предположим, что компания Toshiki открыла филиал на Украине, в результате чего издержки одного заказа сокра­тились до 50 долл. Как это может повлиять на выбор постав­щика видеосистем?

Ответы и решения

Ответы на вопросы: 1 —2, 2 — 1, 3 — 5, 4 —3, 5 —4, 6— 3.

Задача 1. Решение.

Исходные данные:

D = 1500 шт.; Я= 45 руб.; К= 150 руб.; Т= 300 дн.; L = 6 дн.

I. Оптимальный размер заказа

2. Годовые издержки заказа

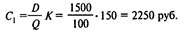
3. Для нахождения точки восстановления запаса, т.е. того уровня запаса, при котором нужно сделать новый заказ, определим суточный спрос:

Тогда точка восстановления запаса R будет равна dL = 5×6 = 30 шт.

Ответы: 1. 100 шт. 2. 2250 руб. 3. 30 шт.

Задача 2. Решение.

Исходные данные:

D = 400 шт.; h = 1 тыс. руб.; К =40 тыс. руб.; Т= 250 дн.; L = 6 дн.

1. Оптимальный размер заказа

2. Ежедневный спрос

Тогда точка восстановле­ния запаса R будет равна dL = 1,6×6 = 9,6 шт.

3. Если издержки хранения запаса равны 1,5 тыс. руб. в день, оптимальный

размер заказа составит

Ответы: 1. 11,3 шт. 2. 9,6 шт. 3. 9,2 шт.

Задача 3. Решение.

Исходные данные:

р = 150 шт.; d = 40 шт.; Н= 8 руб.; К= 100 руб.; T = 250 дн.

Найдем суточные издержки на хранение: h = = 0,032 руб.

1. Оптимальный размер заказа в модели с производством

2. Издержки хранения (годовые)

3. Совокупные издержки за год

Ответы: 1.583,9шт. 2.1712,8руб. 3.3425,4руб.

Задача 4. Решение.

Исходные данные:

D = 3000 шт.; d =10шт.; h =0,4 руб.; K = 25 руб.; b = 0,75 руб.; T = 3000: 10 = 300 дн.

1. Оптимальный размер заказа в модели с дефицитом

2. Максимальный размер запаса

Максимальный дефицит равен Q* – S* = 43,8 – 28,5 = 15,3 шт.

3. Совокупные издержки за год

Ответы: 1. 43,8 шт. 2. 15,3 шт. 3. 3426 руб.

Задача 5. Решение.

Поскольку издержки на хранение зависят от цены товара, а цена товара в каж­дом интервале различна, необходимо определить оптимальный размер заказа для каждого ценового интервала:

Графики совокупных издержек представлены на рис. 7.

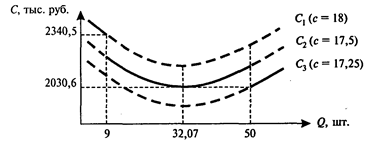
Рис.7

Как видно из графиков, при цене в 18 тыс. руб. оптимальный размер заказа попадает во второй ценовой интервал. Однако при цене в 18 тыс. руб. можно за­казать не более 9 кусков, поэтому мы должны при расчете совокупных издержек С ₁ взять оптимальный размер заказа Q ₁, равный девяти кускам (только при этом размере заказа на первом интервале совокупные издержки будут минимальны):

При цене 17,5 тыс. руб. оптимальный размер заказа Дд равен 32,07 и сово­купные издержки составят

При цене 17,25 тыс. руб. оптимальный размер заказа Q ₃ мы должны взять равным 50, совокупные издержки при этом составят

Проведя анализ совокупных издержек с различными ценовыми скидками, можно сделать вывод о том, что оптимальный размер заказа может быть равен либо 32,07 куска, либо 50 кускам, поскольку и в том и в другом случае совокуп­ные издержки минимальны.

Ответ: 32,07 или 50 шт.

Задача 6. Решение.

Цена со скидкой на товар равна 50×0,97 = 48,5 тыс. руб.

Оптимальный размер заказа при цене 50 тыс. руб.

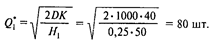
Оптимальный заказ с ценовой скидкой в 3% составит

Найдем совокупные издержки при цене 50 тыс. руб. При этом оптимальный размер заказа мы должны взять равным 80:

При расчете совокупных издержек со скидкой мы должны взять оптимальный размер заказа равным 200:

Можно сделать вывод, что следует воспользоваться скидкой на товар и сде­лать заказ на 200 гарнитуров.

Ответ: Да, следует.

Глава 13. Модели систем массового обслуживания

Цели

Основы знаний об очередях, иногда называемые теорией оче­редей или теорией массового обслуживания, составляют важную часть теории управления производством. Очереди — обычное яв­ление. Они могут носить форму ожидания ремонта автомобиля в центре автосервиса или ожидания студентами консультации у про­фессора. В таблице перечислены некоторые примеры возникно­вения очередей в системах массового обслуживания:

Модели очередей (как и линейное программирование, модели управления запасами, методы сетевого анализа проектов) исполь­зуются и в сфере управления материальным производством, и в сфере обслуживания. Анализ очередей в терминах длины очере­ди, среднего времени ожидания, среднего времени обслуживания и других факторов помогает нам лучше понять принципы орга­низации системы обслуживания. Ожидание пациента в приемной врача и ожидание починки сломанной дрели в ремонтной мастер­ской имеют много общего с точки зрения управления процессом обслуживания. Оба процесса используют человеческие ресурсы и ресурсы оборудования для удовлетворения потребностей клиентов.

Профессиональный менеджер, принимая решение о совершен­ствовании системы массового обслуживания, оценивает измене­ния, возникающие в затратах на функционирование системы и в издержках, связанных с ожиданием клиентов. Можно нанять большое количество сотрудников, которые будут быстро обслуживать клиентов. Так, администратор супермаркета может умень­шить очереди в кассы, увеличивая в часы пик количество продав­цов и кассиров. Для работы в кассах банков или аэропортов в часы пик могут быть привлечены дополнительные сотрудники. Одна­ко снижение времени ожидания обычно сопряжено с издержка­ми на создание и оснащение рабочих мест, с оплатой труда до­полнительного персонала. Эти издержки могут быть весьма зна­чительны.

Можно сэкономить на трудозатратах. Но тогда клиент может не дождаться обслуживания или потерять охоту вернуться еще раз. В последнем случае система массового обслуживания будет нести потери, которые можно назвать издержками ожидания. В некоторых системах обслуживания, например в скорой помо­щи, затраты, связанные с длительным ожиданием, могут оказать­ся чрезвычайно высокими. Основной экономический принцип совершенствования систем массового обслуживания состоит в оценке общих ожидаемых затрат, включающих затраты на обслу­живание и потери, которые несет система в результате ожидания клиента.

После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь определять и использовать для экономи­ческого анализа следующие понятия:

• система массового обслуживания;

• заявка;

• очередь;

• темп поступления заявок;

• темп обслуживания;

• среднее время, которое заявка проводит в очереди;

• средняя длина очереди;

• среднее время, которое заявка проводит в системе обслужи­вания;

• среднее число клиентов в системе обслуживания;

• издержки функционирования системы обслуживания;

• издержки ожидания.

Модели

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: