Открытая транспортная задача.

а) 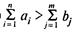— излишек продукта

Способ сведения к замкнутой задаче. Пусть b_{m +1} — величина избытка продукции, т.е. - штраф за еди­ницу продукта, не реализованного в пункте i; у_i — количество про­дукта, не реализованного в пункте i.

Замкнутая транспортная задача имеет вид

б) — дефицит продукта.

Способ сведения к замкнутой задаче. Пусть а_{n +1} — величина дефицита продукции, т.е. - штраф за еди­ницу продукта, недопоставленного в пункт j; у_j — количество про­дукта, недопоставленного в пункту.

Замкнутая транспортная задача имеет вид

3. Транспортная задача с запретами. Пусть Е — множество пар индексов (ij), таких, что из пункта i в пункт j допускается транс­портировка продукта. Между любыми другими двумя пунктами транспортировка не допускается.

Пусть М— большое число, например

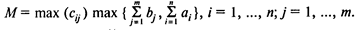
Тогда

В оптимальном плане { } транспортной задачи при ограничениях (2)—(4) x_ij = 0, если (i,j) Ï Е.

4. Транспортная задача с фиксированными перевозками. Если объем перевозок между пунктами i и j задан, то в задаче (1)—(4) вводится дополнительное ограничение: x_ij = v_ij, где v_ij — заданный объем перевозок.

5. Транспортная задача с ограничениями на пропускную способ­ность. Если объем перевозок из пункта i в пункт j ограничен ве­личиной w_ij, то в задаче (1)—(4) вводится дополнительное огра­ничение: x_ij £ w_ij.

6. Транспортная задача с фиксированными доплатами. Предпо­ложим, что в открытой транспортной задаче имеет место дефицит продукта и для его устранения в пунктах i = п + 1,..., k воз­можно создание новых мощностей d_i.

Пусть переменные z_i = 1, если в пункте i (i = п + 1,..., k) вво­дятся мощности d_i и z_i = 0, если в пункте i мощности не вводят­ся. Издержки на ввод мощностей d, в пункте i (i = n + 1,..., k)составляют и_i.

С учетом возможности создания новых мощностей транспорт­ная задача может быть записана в следующем виде:

Здесь (5) — целевая функция (минимум затрат на транспортиров­ку и ввод мощностей);

(6) — ограничения по величине предложения в каждом су­ществующем пункте производства;

(7) — ограничения по величине предложения в каждом но­вом пункте производства;

(8) — ограничения по величине спроса в каждом пункте по­требления;

(9) — условия неотрицательности объемов перевозок.

Помимо непрерывных переменных x_ij в модель включены бу­левы переменные z_i,. Задача (5)—(9) является задачей линейного программирования со «смешанными» переменными.

Все приведенные модели описывают транспортную задачу в виде задачи линейного программирования. В такой форме она может быть решена стандартными средствами линейного програм­мирования, например симплекс-методом.

Для решения транспортной задачи могут быть использованы также и менее трудоемкие (по объему вычислений) алгоритмы, например метод потенциалов.

Большинство специальных алгоритмов решения транспортной задачи использует исходную информацию в форме транспортной таблицы:

Оптимальный план перевозок имеет вид

Примеры

Пример 1. Определение плана перевозок.

Компания, занимающаяся добычей железной руды, имеет че­тыре карьера. Производительность карьеров соответственно 170, 130, 190 и 200 тыс. т ежемесячно. Железная руда направляется на три принадлежащие этой компании обогатительные фабрики, мощности которых соответственно 250, 150 и 270 тыс. т в месяц.

Транспортные затраты (в тыс. руб.) на перевозку 1 тыс. т руды с карьеров на фабрики указаны в следующей таблице:

Определите план перевозок железной руды на обогатительные фабрики, который обеспечивает минимальные совокупные транс­портные издержки.

Вопросы:

1. Сколько руды следует перевозить с карьера 1 на обогатитель­ную фабрику 2?

2. Сколько руды следует перевозить с карьера 4 на обогатитель­ную фабрику 1?

3. Какой объем мощностей по добыче руды окажется неис­пользованным?

4. Каковы минимальные совокупные транспортные издержки?

Решение. Транспортная таблица имеет следующий вид:

Ниже приведены результаты расчетов — объемы перевозок и остаток невывезенной руды (в тыс. т):

В следующей таблице до косой черты указаны объемы перево­зок, после черты — соответствующие издержки:

Минимальные совокупные издержки составляют 2710 тыс. руб.

Ответы: 1.10 тыс. т. 2. 60 тыс. т.

3. 20 тыс. т. 4. 2710 тыс. руб.

Пример 2. Задача агрегированного планирования.

Компания «Родник» производит и реализует в России концен­трат для приготовления фруктового напитка «Солнышко». Про­изводство осуществляется на заводе в Самаре. Отдел сбыта ком­пании «Родник» заключил договоры на поставку концентрата в следующем объеме: апрель — 55 т, май — 70 т, июнь — 75 т. При работе в две смены на собственном оборудовании компания мо­жет производить в месяц до 50 т концентрата. Если использовать сверхурочное время, можно увеличить объем производства на 5 т в месяц. В апреле начальный запас концентрата на складе соста­вит 10 т.

Нетрудно видеть, что даже при использовании сверхурочного времени и складских запасов концентрата выполнить договоры не удастся. Поэтому в целях выполнения договорных обязательств принято решение арендовать оборудование акционерного общест­ва «Волжанка». За счет аренды появляется возможность увеличить производство концентрата на 12 т в апреле, на 12 т в мае и на 10 т в июне.

Известно, что производство 1 т концентрата в регулярном ре­жиме двухсменной работы оборудования обходится в 60 тыс. руб. При использовании сверхурочного времени издержки увеличива­ются на 20 тыс. руб. за тонну.

Производство 1 т концентрата на арендованном оборудовании обходится в 90 тыс. руб. Издержки хранения 1 т концентрата в течение месяца — 1 тыс. руб.

Договоры предусматривают штрафные санкции в случае несвое­временной поставки концентрата. При задержке поставок на один месяц компания должна будет заплатить штраф в размере 3 тыс. руб. за тонну.

Составьте план использования собственных и арендуемых мощностей для компании «Родник» на каждый месяц второго квартала.

Вопросы:

1. Чему равно значение коэффициента транспортной таблицы, соответствующего регулярному использованию собственных мощностей компании в апреле для удовлетворения спроса на май?

2. Чему равно значение коэффициента транспортной таблицы, соответствующего регулярному использованию собственных мощностей компании в мае для удовлетворения спроса на апрель?

3. При каких минимальных издержках можно выполнить за­ключенные на второй квартал договоры?

4. Какое количество концентрата следует производить в апре­ле на арендуемом оборудовании?

5. Какой размер штрафных санкций за несвоевременную по­ставку концентрата предусмотрен планом?

6. Какая величина запаса концентрата на начало июня преду­смотрена планом?

7. Чему равны издержки выполнения договоров на июнь?

Решение. Для составления плана используем модель транспорт­ной задачи. Транспортная таблица в этом случае имеет следу­ющий вид:

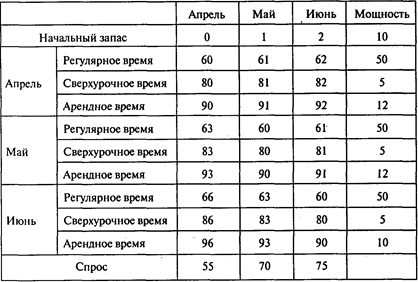
Например, значение 1 коэффициента в первой строке транс­портной таблицы (при использовании начального запаса для удов­летворения спроса в мае) показывает, что издержки хранения 1 т концентрата в течение месяца (апрель) составят 1 тыс. руб.

Значение 2 коэффициента в первой строке (при использовании начального запаса для удовлетворения спроса в июне) показыва­ет, что издержки хранения 1 т концентрата в течение двух меся­цев (апрель, май) составят 2 тыс. руб.

Значение 60 коэффициента во второй строке матрицы (при регулярном использовании собственных мощностей в апреле для удовлетворения спроса в апреле) соответствует производственным издержкам — 60 тыс. руб./т.

Значение 66 коэффициента в восьмой строке матрицы (при регулярном использовании собственных мощностей в июне для выполнения договоров, заключенных на апрель) превышает про­изводственные издержки (60 тыс. руб./т) на величину штрафных санкций (6 тыс. руб./т) за несвоевременную (с опозданием на два месяца) поставку каждой тонны концентрата.

Используя приведенную выше транспортную таблицу, получа­ем следующее решение задачи:

В соответствии с этим решением из 50 т концентрата, произ­веденного на регулярных мощностях в апреле, 45 т следует исполь­зовать при выполнении договоров, заключенных на апрель, 5т— при выполнении договоров, заключенных на май.

В апреле на арендуемых мощностях следует произвести 3 т кон­центрата. При этом резерв мощности составит 9 т.

В мае арендуемые мощности следует использовать полностью (12 т). При этом 2 т из этих 12 следует использовать для выпол­нения договоров, заключенных на май, а 10 т — для выполнения договоров, заключенных на июнь.

В следующей таблице минимальные совокупные издержки (12 473 тыс. руб.), соответствующие оптимальному плану исполь­зования мощностей, специфицированы по различным статьям расходов:

Окончание таблицы

При использовании регулярных мощностей удельные производ­ственные издержки составляют 60 тыс. руб./т.

В случае регулярного использования собственных мощностей в апреле для выполнения договоров, заключенных на май, значение коэффициента транспортной таблицы превышает производствен­ные издержки (60 тыс. руб./т) на величину удельных затрат на хранение концентрата (1 тыс. руб./т). Значение коэффициента рав­но 61 тыс. руб./т.

В случае регулярного использования собственных мощностей в мае для выполнения договоров, заключенных на апрель, значе­ние коэффициента транспортной таблицы превышает производ­ственные издержки (60 тыс. руб./т) на величину штрафных санк­ций (3 тыс. руб./т) за несвоевременную (с опозданием на один месяц) поставку каждой тонны концентрата. Значение коэффици­ента равно 63 тыс. руб./т.

Ответы: 1. 61 тыс. руб./т. 2. 63 тыс. руб./т. 3. 12 473 тыс. руб. 4. 3 т. 5. 0 руб. 6. 10 т. 7. 5210 тыс. руб.

Вопросы

Вопрос 1. Транспортная задача является частным случаем за­дачи:

1) линейного программирования;

2) регрессионной;

3) статистической;

4) имитационной;

5)о назначениях.

Вопрос 2. Рассматривается открытая транспортная задача, в ко­торой суммарные запасы M поставщиков больше, чем суммарные потребности N потребителей. На сколько увеличится число пере­менных задачи после приведения ее к замкнутому виду?

Варианты ответов:

2) на N; 2) на М; 3)на N + M; 4) на N × М; 5) останется без изменения.

Вопрос 3. Рассматривается транспортная задача, сформулиро­ванная как задача линейного программирования. Объемы перево­зок измеряются в тоннах, значение целевой функции — в рублях. В каких единицах измеряется значение коэффициента целевой функции?

Варианты ответов:

1) руб.; 2) руб./т; 3) т/руб.; 4) т; 5) безразмерная величина.

Вопрос 4. Рассматривается открытая транспортная задача, в ко­торой суммарные запасы M поставщиков меньше, чем суммарные потребности N потребителей. На сколько увеличится число пере­менных задачи после приведения ее к замкнутому виду?

Варианты ответов:

1) на N; 2)на М; 3)на N+M; 4) на N × М; 5) останется без изменения.

Вопрос 5. В открытой транспортной задаче:

1) величина совокупного предложения больше величины сово­купного спроса;

2) величина совокупного предложения меньше величины со­вокупного спроса;

3) величина совокупного предложения равна величине совокуп­ного спроса;

4) величина совокупного предложения не равна величине со­вокупного спроса;

5) ограничения сформулированы в виде неравенств.

Задачи

Задача 1. Фирма по прокату автомобилей «Золотое кольцо Рос­сии» собирает заявки на аренду во всех городах центра России. Клиент имеет возможность получить автомобиль в любом удоб­ном для него населенном пункте и оставить его в любом месте, где он заканчивает путешествие, в том числе и в своем родном го­роде. Работники фирмы забирают оставленные автомобили и пе­регоняют их для передачи новым клиентам.

Сейчас 4 автомобиля компании оставлены в Клину, 3 — в Ро­стове Великом, 6—в Ярославле и 1 — в Серпухове.

Имеются заказы на 5 автомобилей во Владимире, на 3 автомо­биля в Санкт-Петербурге и на 6 автомобилей в Москве.

Расстояния между городами (в км) приведены в следующей таблице:

Составьте план, по которому следует перегонять автомобили новым клиентам. Ориентируйтесь на минимизацию расстояния, которое пройдут все перегоняемые автомобили.

Вопросы:

1. Чему равно минимальное расстояние, которое должны прой­ти все автомобили?

2. Сколько автомобилей следует перегнать в Москву из Яро­славля?

3. На сколько увеличится минимальное расстояние, которое должны пройти все автомобили, если дополнительно ста­ло известно, что еще один автомобиль оставлен в Серпухо­ве и еще один клиент появился в Москве?

Задача 2. Компания «Уют» производит пластмассовую мебель для отдыха на открытом воздухе. Основной продукт компании — стулья. Производство находится в Можайске, Наро-Фоминске и Туле. Сейчас на складе в Можайске находятся 7250 стульев, в Наро-Фоминске — 10 150, в Туле — 4350.

Основными потребителями продукции компании «Уют» явля­ются фирмы по оптовой продаже в Москве, Санкт-Петербурге, Минске и Воронеже. Сейчас эти фирмы готовы закупить соответ­ственно 8800, 5800, 2900 и 2100 стульев.

Удельные затраты на перевозку стульев (в руб./шт.) указаны в следующей таблице:

Помогите компании «Уют» составить план транспортировки стульев потребителям.

Вопросы:

1. Чему равны минимальные издержки на перевозку всех стульев?

2. Сколько стульев компания должна перевозить в Москву из Можайска?

3. Какое количество стульев останется на складе в Туле?

4. Стало известно, что для сбыта в Москве не годятся стулья, сделанные в Туле, а для сбыта в Санкт-Петербурге — стулья из Наро-Фоминска. Не подходит цвет стульев. Составьте новый план перевозок с учетом этих условий. На сколько рублей увеличатся при этом совокупные транспортные из­держки?

Задача 3. Компания, занимающаяся добычей железной руды, имеет четыре карьера С ₁¸ С ₄ (см. пример 1). Производительность карьеров соответственно 170, 150, 190 и 200 тыс. т ежемесячно. Железная руда направляется на три принадлежащие этой компа­нии обогатительные фабрики S ₁ ¸ S ₃, мощности которых соответ­ственно 250, 150 и 270 тыс. т в месяц.

Транспортные затраты (в тыс. руб.) на перевозку 1 тыс. т руды с карьеров на фабрики указаны в следующей таблице:

Определите план перевозок железной руды на обогатительные фабрики, который обеспечивает минимальные совокупные транс­портные издержки.

Вопросы:

1. Сколько руды следует перевозить с карьера С ₁ на обогати­тельную фабрику S ₂?

2. Сколько руды следует перевозить с карьера С ₄ на обогати­тельную фабрику S ₃?

3. Какова общая минимальная стоимость перевозок?

4. Стало известно, что поставки с карьера С ₁ на обогатитель­ную фабрику S ₂ нужно ограничить объемом 50 тыс. т. К тому же из-за плохого состояния дороги перевозки с карьера С ₄на обогатительную фабрику S ₃ невозможны. Определите но­вый план перевозок, учитывающий эти условия. На сколь­ко возрастет стоимость перевозок?

5. Сколько руды следует перевозить с карьера С ₄ на обогати­тельную фабрику S ₂ с учетом дополнительной информации?

Задача 4. Фирма «Мойдодыр» оценила спрос на производимый ею лосьон для каждого из четырех следующих месяцев: 100 ящи­ков в июне, 140 — в июле, 170 — в августе и 90 — в сентябре. Без использования сверхурочного времени фирма может производить до 125 ящиков лосьона в месяц. В сверхурочное время может быть произведено еще 25 ящиков в месяц, но производство каждого ящика обойдется при этом на 1 тыс. руб. дороже. Хранение одно­го ящика в течение месяца обходится в 100 руб.

Используя модель транспортной задачи, определите, сколько ящиков лосьона следует производить в каждый из этих месяцев, что­бы удовлетворить спрос с минимальными совокупными затратами.

Вопросы:

1. Сколько ящиков лосьона следует произвести в июне?

2. Сколько часов сверхурочного времени следует использовать в сентябре?

Задача 5. Фирма «Время — вперед» хочет разработать план сборки компьютеров. Прогноз спроса на компьютеры для каждо­го квартала следующего года показан в таблице:

При работе в одну смену фирма может каждый квартал соби­рать 1200 компьютеров. Издержки по сборке одного компьютера составляют 10 тыс. руб. Если ввести вторую смену, то ежеквар­тально можно собирать еще 800 компьютеров. Однако сборка каж­дого компьютера во вторую смену обходится дороже — 11 тыс. руб. Компьютер может быть произведен в одном квартале, а сбыт — в любом из последующих кварталов. В этом случае хранение каж­дого компьютера обходится в 500 руб. за квартал.

Составьте план производства, используя модель транспортной задачи.

Вопросы:

1. Сколько компьютеров следует собрать в первом квартале, чтобы удовлетворить спрос с минимальными совокупными затратами?

2. На сколько процентов следует использовать мощности вто­рой смены в первом квартале?

3. Сколько компьютеров следует собрать во втором квартале?

4. Сколько компьютеров следует собрать во втором квартале во вторую смену для сбыта в третьем квартале?

5. Каковы минимальные издержки?

Ситуации

Ситуация 1. «Фургоны под жилье».

Фирма «Фургоны под жилье», возглавляемая Тони Риццо, за­нимается переделкой стандартных фургонов в бунгало для жилья. В зависимости от объема работы такая переделка обходится заказ­чику от 1000 до 5000 долл. За последние четыре года Тони Риццо расширил свое небольшое дело в Гери, Индиане и открыл фили­алы в Чикаго, Милуоки, Миннеаполисе и Детройте.

Нововведения — основной фактор, позволивший добиться ус­пеха в превращении маленькой фирмы в процветающее предпри­ятие. Тони удалось придумать и создать множество приспособле­ний, пользующихся повышенным спросом у покупателей фурго­нов под жилье, например душевую кабину, сконструированную Тони через шесть месяцев после того, как была создана фирма. Эта кабина занимает вдвое меньше места, чем обычная, и может быть размещена не только в фургонах любого типа, но и в других мес­тах рядом с фургоном. Душевая кабина сделана из фибергласа и снабжена вешалкой для полотенец, встроенным душем и держа­телем для шампуня. На производство каждой душевой кабины уходит два галлона фибергласа и три часа рабочего времени.

Большинство душевых кабин производилось в Гери, где была основана фирма. Фабрика в Гери может выпускать до 300 душе­вых кабин в месяц, но этого количества всегда было недостаточ­но. Все четыре магазина фирмы выражали недовольство недоста­точным объемом поставок душевых кабин. К тому же Тони отда­вал трем магазинам преимущество в снабжении по сравнению с четвертым в Миннеаполисе, так как последний находился даль­ше всех от Гери. Это приводило в бешенство менеджера фирмы в Миннеаполисе, и после длительных дискуссий Тони решил от­крыть другую фабрику по производству душевых кабин в Форт Вайне. Эта фабрика способна производить 150 душевых кабин в месяц. Новая фабрика в Форт Вайне все же не смогла полностью обеспечить спрос на душевые кабины. Тони знал, что в ближай­шие годы спрос на них может только увеличиваться. После кон­сультаций со своим адвокатом и банкиром Тони принял решение как можно скорее открыть две новые фабрики. Каждая из них должна иметь такую же производительность, как фабрика в Форт Вайне. Был проведен предварительный анализ возможных мест расположения новых фабрик, и Тони решил, что две новые фаб­рики могут быть размещены в одном из трех мест: Детройте (штат Мичиган), Рокфорде (штат Иллинойс) или Мэдисоне (штат Вис­консин). Тони знал, что выбрать место для расположения новых фабрик непросто. Важно учесть транспортные издержки для каж­дого возможного варианта размещения. Магазином в Чикаго управлял Билл Барч. Этот фирменный магазин был первым филиалом, открытым Тони, и его возмож­ности превосходили возможности других магазинов. Фабрика в

Гери поставляла туда 200 душевых кабин в месяц, в то время как Билл знал, что может продать 300 кабин. Издержки на транспорти­ровку одной душевой кабины из Гери в Чикаго составляют 10 долл., и, несмотря на то что удельные транспортные издержки от Форт Вайна вдвое выше, Билл всегда хотел добиться от Тони поставки оттуда 50 кабин. Две новые фабрики могли бы обеспечить Биллу поставку тех 100 кабин, которых ему недоставало. Транспортные издержки, разумеется, будут зависеть от того, где Тони откроет фабрики. Для Детройта удельные транспортные издержки соста­вят 30 долл., для Рокфорда — 5 долл., а для Мэдисона — 10 долл.

Вилма Джексон, менеджер фирменного магазина в Милуоки, выражала недовольство недостаточным объемом поставок душе­вых кабин. В настоящее время спрос составлял 100 кабин и лишь наполовину удовлетворялся поставками с фабрики Форт Вайна. Она не могла понять, почему Тони не присылает ей все 100 ка­бин из Гери. Удельные транспортные издержки для Гери состав­ляют 20 долл., в то время как для Форт Вайна — 30 долл. Вилма надеялась, что одним из мест размещения новой фабрики станет Мэдисон. Тогда она сможет получать необходимое количество душевых кабин при транспортных издержках всего 5 долл. Если не Мэдисон, то новая фабрика в Рокфорде тоже может удовлет­ворять потребности ее магазина. Правда, транспортные издерж­ки в этом случае вдвое выше, чем для Мэдисона. Вилма не пита­ет надежды на поставки из Детройта. Если новую фабрику откро­ют там, то транспортные издержки составят 40 долл.

Управляющим фирменным магазином в Миннеаполисе был Том Пански. Он получал 100 душевых кабин из Гери. Спрос со­ставлял 150 шт. Том имел наибольшие удельные транспортные издержки. Для Гери они составляли 40 долл. Если бы душевые кабины транспортировались из Форт Вайна, удельные транспорт­ные издержки были бы на 10 долл. больше. Том надеялся, что в Детройте новой фабрики не будет, так как в этом случае транс­портные издержки составили бы 60 долл. за одну кабину. Для Рок­форда и Мэдисона они будут 30 и 35 долл. соответственно.

Положение магазина в Детройте было таким же, как в Милуо­ки, только спрос удовлетворялся всего наполовину. Все 100 душе­вых кабин, которые получает Детройт, поступают из Форт Вайна. Для Форт Вайна транспортные издержки составляли 15 долл. за штуку, а для Гери — 25 долл. Дик Лопес, менеджер магазина в Дет­ройте, высоко оценивал шансы строительства новой фабрики в Детройте. Она размещалась бы в пригороде, и удельные транспорт­ные издержки составили бы всего 2 долл. Он мог бы получать 150 душевых кабин с новой фабрики в Детройте, а оставшиеся 50 кабин — из Форт Вайна. Два других места размещения фабри­ки представлялись ему неудачными. Рокфорд имел удельные транспортные издержки 35 долл., а Мэдисон — 40 долл.

Перед тем как созвать на совещание менеджеров своих мага­зинов, Тони несколько недель размышлял о том, где разместить новые фабрики. Проблема была комплексной, но цель ясна — ми­нимизация общих издержек. Совещание, на котором присутство­вали все менеджеры, кроме Вилмы, состоялось в Гери.

Тони: Благодарю за то, что приехали. Как вам известно, я ре­шил открыть две новые фабрики в Рокфорде, Мэдисоне или Дет­ройте. Это, разумеется, изменит положение, и вы сможете полу­чить недостающее количество душевых кабин. Я знаю, что вы могли бы продавать больше, чем сейчас, и чувствую себя ответ­ственным за эту ситуацию.

Дик: Тони, я много размышлял над этой проблемой и считаю, что местом размещения одной из новых фабрик должен стать Детройт. Сейчас я получаю лишь половину того количества кабин, которое могу продать. Мой брат Леон очень заинтересован в пус­ке фабрики, и я думаю, он хорошо справился бы с этой работой.

Том: Дик, я убежден, что Леон был бы на высоте, и я знаю, какие у вас проблемы из-за спада в автомобильной промышлен­ности. Однако нам следует принимать во внимание издержки, а не персоналии. Я убежден, что новые фабрики надо открыть в Рокфорде и Мэдисоне. Мой магазин слишком удален от других фабрик, и такое размещение позволит существенно снизить транс­портные издержки.

Дик: Может быть, это и верно, но надо учитывать другие фак­торы. Детройт — один из основных потребителей фибергласа, и я интересовался ценами на него. Новая фабрика в Детройте сможет получать фиберглас на 2 долл. дешевле, чем в любом другом месте.

Том: В Мэдисоне прекрасная рабочая сила благодаря студен­там Мэдисонского университета. Студенты — отличные рабочие, и они согласятся получать на 1 долл. в час меньше.

Билл: Хватит спорить. Ясно, что так мы не договоримся о том, где размещать новые фабрики. Давайте проголосуем и выберем два города.

Тони: Не думаю, что голосование — лучший способ выбора. К то­му же Вилма не смогла приехать. Нам следовало бы учесть все эти факторы формальным образом.

Задания

1. Оцените избранную Тони стратегию поставок при двух дей­ствующих фабриках в предположении, что существующий объем поставок душевых кабин в магазины фирмы не мо­жет быть уменьшен. Обеспечивает ли она минимальные транспортные издержки?

2. Разработайте модель математического программирования, учитывающую все факторы, влияющие на принятие решения.

3. Проведите расчеты и определите наилучшие места для раз­мещения новых фабрик. Обоснуйте ваши выводы результа­тами расчетов.

(Переработано из: Render В., Stair R. Quantitative Analysis for Manage­ment. 4th ed. — Boston: Allyn and Bacon, 1991)

Ситуация 2. «Мечта автомобилиста».

Фирма «Мечта автомобилиста» изготовляет сменные стекла для всех типов российских автомобилей. Фирма разработала и внедри­ла сложную систему прогнозирования спроса, использующую дан­ные за последние годы для определения фактора сезонности и долгосрочных трендов. В таблице представлен агрегированный (для всех видов стекол) понедельный прогноз спроса на текущий год (в кг):

Фирма «Мечта автомобилиста» использует прогнозы спроса для планирования объемов производства. При составлении плана про­изводства фирма должна учесть издержки найма или увольнения рабочих, оплату сверхурочных, субподряда, издержки хранения готовой продукции.

Издержки хранения составляют 0,12 руб. за 1 кг в неделю. Со­гласно смете производственные издержки в настоящее время рав­ны 20 руб. за 1 кг в неделю. Сумма затрат на каждого нанимаемо­го рабочего, приходящаяся на 1 кг продукции, составляет 5,63 руб. (данные издержки рассчитываются на основе затрат на обучение и средней производительности труда одного рабочего). Сумма за­трат на каждого увольняемого, приходящаяся на 1 кг продукции, составляет 15,73 руб. (рассчитывается исходя из размера компен­сационных выплат при увольнении и с учетом уменьшения пре­стижа фирмы). При нормальном режиме работы (без сверхуроч­ных) фирма может производить до 1900 кг стекла в неделю. Кро­ме того, может быть произведено до 100 кг при использовании субподряда, и еще 250 кг стекла в неделю «Мечта автомобилиста» может произвести на своих мощностях сверхурочно. Издержки для стекла, производимого сверхурочно, на 8 руб. за 1 кг больше, чем для производимого в обычное время. Издержки производства по субподряду на 2 руб. за 1 кг больше, чем при производстве сверх­урочно (т.е. на 10 руб. за 1 кг выше, чем при производстве в обыч­ном режиме).

В настоящее время запасы стекла на складе составляют 73 кг. Производство работает на полную мощность, выпуская 1900 кг продукции в неделю.

Задание

Составьте агрегированный план производства для фирмы «Мечта автомобилиста» в целях минимизации совокупных из­держек. Примите во внимание различные предположения и ва­рианты реализации производственной политики и покажите, как эти различия отразятся на вариантах планов.

Ответы и решения

Ответы на вопросы: 1 —1, 2 — 2, 3 —2, 4 — 1, 5 —4.

Задача 1. Решение.

С учетом исходной информации транспортная таблица имеет вид

Результаты расчетов (оптимальный план доставки автомобилей):

С учетом дополнительной информации транспортная таблица имеет вид

Оптимальный план доставки автомобилей:

Ответы: 1. 3810 км. 2. Два автомобиля. 3. На 150 км.

Задача 2. Решение.

Транспортная таблица имеет вид

Результаты расчетов (оптимальный план транспортировки стульев):

С учетом запретов на перевозки имеем следующую транспортную таблицу, где М — большое число:

С учетом дополнительных ограничений на перевозки модель имеет вид

Результаты расчетов:

Ответы: 1. 130 тыс. т. 2. 180 тыс. т. 3. 2930 тыс. руб. 4. На 360 тыс. руб. 5. 140 тыс. т.

Задача 4. Решение.

Транспортная таблица имеет вид (издержки производства в основное время принимаются равными нулю; буква M означает запрет соответствующих «пере­возок»)

Результаты расчетов:

Ответы: 1. 125 ящиков. 2. 0 часов.

Задача 5. Решение.

Транспортная таблица имеет вид

План производства:

Ответы: 1. 1300 компьютеров. 2. На 12,5%. 3. 2000 компьютеров. 4. 800 компьютеров. 5. 76700 тыс. руб.

Глава 6. Задача о назначениях

Цели

В процессе управления производством зачастую возникают за­дачи назначения исполнителей на различные виды работ, напри­мер: подбор кадров и назначение кандидатов на вакантные долж­ности, распределение источников капитальных вложении между различными проектами научно-технического развития, распреде­ление экипажей самолетов между авиалиниями.

Задачу о назначениях можно сформулировать следующим об­разом. Необходимо выполнить N различных работ. Для их выпол­нения можно привлечь N рабочих. Каждый рабочий за определен­ную плату готов выполнить любую работу. Выполнение любой работы следует поручить одному рабочему. Требуется так распре­делить работы между рабочими, чтобы общие затраты на выпол­нение всех работ были минимальными.

После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь определять и использовать для экономи­ческого анализа:

• задачу о назначениях в стандартной форме;

• открытую задачу о назначениях;

• таблицу задачи о назначениях;

• матрицу назначений;

• эффективность назначений.

Модели

Пусть т — количество работ.

Задача о назначениях в стандартной форме. При рассмотрении задачи о назначениях в стандартной форме предполагается, что количество рабочих равно количеству работ.

Обозначения:

с_ij — показатель эффективности назначения i -го рабочего на j -й работе, например издержки выполнения i- м рабочим j -й работы;

x_ij — переменная модели (х_ij = 1, если i -й рабочий использует­ся на j -й работе, и x_ij = 0 в противном случае).

Модель задачи о назначениях:

Здесь (1) — целевая функция (минимум издержек на выполнение всех работ);

(2) — система ограничений, отражающая следующие усло­вия:

а) каждая работа должна быть выполнена одним рабо­чим;

б) каждый рабочий может быть привлечен к одной работе;

(3) — условия неотрицательности переменных.

При решении задачи о назначениях исходной информацией является таблица задачи о назначениях с={ с_ij }, элементами ко­торой служат показатели эффективности назначений. Для задачи о назначениях, записанной в стандартной форме, количество строк этой таблицы совпадает с количеством столбцов:

Результатом решения задачи о назначениях (1)—(3) является вектор х * = { }, компоненты которого — целые числа.

Оптимальный план задачи о назначениях (1)—(3) можно пред­ставить в виде квадратной матрицы назначений, в каждой строке и в каждом столбце которой находится ровно одна единица. Та­кую матрицу иногда называют матрицей перестановок. Значение целевой функции (1), соответствующее оптимальному плану, на­зывают эффективностью назначений.

Задача о назначениях в открытой форме. Задача о назначени­ях в открытой форме возникает тогда, когда количество рабочих не равно количеству работ. В этих случаях задача может быть пре­образована в задачу, сформулированную в стандартной форме.

Пусть, например, количество рабочих п превышает количество работ т.

Введем дополнительные фиктивные работы с индексами j = w + 1,..., п. Коэффициенты таблицы назначений с_ij, i = 1,..., п; j = т + 1,..., п, положим равными нулю. В этом случае получаем задачу, сформулированную в стандартной форме. Если в опти­мальном плане этой задачи = 1 при j = т + 1,..., п, то испол­нитель i назначается на выполнение фиктивной работы, т.е. ос­тается без работы. Заметим, что оптимальное значение целевой функ­ции исходной задачи совпадает с оптимальным значением задачи, приведенной к стандартной форме. Поэтому эффективность на­значений в результате такого преобразования не меняется.

Следует особо отметить, что задача о назначениях является частным случаем транспортной задачи, в которой количество пунк­тов производства совпадает с количеством пунктов потребления, а все величины спроса и величины предложения равны.

Примеры

Пример 1. Распределение работ.

Фирма получила заказы на разработку пяти программных про­дуктов. Для выполнения этих заказов решено привлечь пятерых наиболее опытных программистов. Кажды

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: