Главная | Обратная связь | Поможем написать вашу работу!

Исследование и теоретическое обоснование процесса искривления скважин в анизотропных породах при алмазном бурении

Поскольку теории, базирующиеся на асимметрии скола горной породы под торцом инструмента, не дают удовлетворительного обоснования причин искривления скважин в анизотропных породах, для ответа на поставленные вопросы следует обратиться к процессу силового взаимодействия инструмента и породы.

Для того чтобы скважина отклонялась от заданного направления, на нее должна действовать поперечная сила. Поскольку появление этой силы не может быть объяснено асимметричной формой лунки разрушения, должен быть иной принцип ее формирования. Описанные выше эксперименты бурения на комбинированных кернах позволили предположить, что искривление скважин зависит от величины сил, действующих на породоразрушающий инструмент со стороны породы в плоскости, перпендикулярной продольной оси инструмента.

Рис. 11. 40. Схема силовых взаимодействий породоразрушающего инструмента с анизотропной горной породой

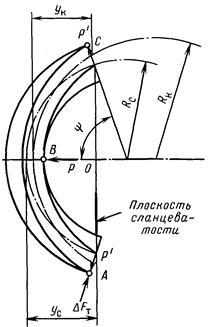
Рассмотрим схему силового взаимодействия породоразрушающего инструмента с образцом анизотропной породы (рис. 11. 40). Основная идея здесь сводится к следующему. Резец породоразрушающего инструмента, перемещающийся по часовой стрелке от точки H до точки G (по дуге HAG), движется в направлении восстания плоскости сланцеватости и, таким образом, вслед отдельным кристаллам, но встречает их под разными углами, что обусловливает неодинаковую силу сопротивления породы этому перемещению в различных точках. От точки G до точки H, двигаясь по дуге GBH, резец перемещается в направлении падения плоскости сланцеватости, причем в точках G и H сопротивление перемещению минимально (если рассматривать дугу GBH), а в точке B сопротивление наибольшее.

Нетрудно заметить, что сумма всех сил, действующих на коронку параллельно x, равна

. (11. 42)

Причем, если сопротивление породы перемещению резца в направлении восстания плоскости сланцеватости меньше, чем в противоположном направлении, то результирующая сила сопротивления DF_т будет расположена так, как это показано на рис. 2. 6, а скважина должна отклоняться в сторону восстания плоскости сланцеватости.

Для того чтобы объяснить наличие отклоняющей силы при встрече плоскости сланцеватости под острым углом, вспомним некоторые общие принципы из теории разрушения горных пород. Дифференцируем этот процесс на составляющие и сопоставим их в условиях перемещения резца в направлении восстания плоскости сланцеватости и в противоположном направлении.

Известно, что процесс алмазного бурения сопровождается погружением резца в породу под действием осевой нагрузки, молекулярным взаимодействием резца и горной породы, пластическим оттеснением некоторой части породы с пути движения резца, упругой деформацией некоторой части породы с последующим восстановлением формы и размеров выступающих частей, скалыванием породы передней гранью резца, - это не полный перечень процессов, которые следует рассматривать в данном случае. Если рассматривать величину погружения резца в породу, ориентируясь на угол встречи плоскости сланцеватости, то она должна быть одинакова для всех точек коронки, во всяком случае в начальный момент.

Силы молекулярного взаимодействия также не зависят от направления вращения инструмента - вслед плоскости сланцеватости или навстречу этой плоскости, поскольку молекулярные силы зависят от притягиваемых масс и расстояния между ними.

Также одинакова и величина пластического оттеснения породы при различных направлениях встречи плоскости сланцеватости, а вот затраты на упругую деформацию выступающих не разрушенных частей породы зависят от направления перемещения резца. В том случае, когда резец скользит вслед наклонным кристаллам (рис. 11. 41, а), вершины последних легко пригибаются и пропускают резец, а при движении резца навстречу кристаллам (Рис. 11. 41, б) для пропуска резца вершина кристалла должна деформироваться на большую величину либо должна нарушиться его сплошность. И в том, и в другом случаях затраты энергии на преодоление препятствия при перемещении резца навстречу наклонному кристаллу больше, чем при перемещении резца вслед наклонному кристаллу.

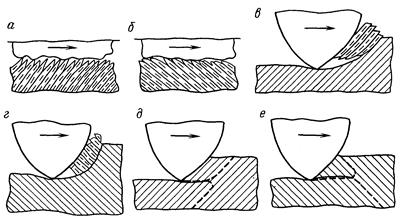
Рис. 11. 41. Схемы взаимодействия резца и породы при перемещении резца: а, б - при упругом деформировании выступающих частей породы; в, г - при скалывании пород передней гранью резца; д, е - при образовании опережающей трещины с различным характером ветвления

Аналогично распределяются затраты энергии на скалывание некоторой части породы передней гранью резца (рис. 11. 41, в, г). Известно, что внутри слойка породы отдельные ее элементы удерживаются друг относительно друга с помощью преимущественно ионно-ковалентных или ковалентно-ионных связей, а слойки породы притягиваются друг к другу посредством молекулярных связей, которые на один - два порядка слабее ионных и ковалентных. Это и обусловливает наличие плоскостей скольжения в горных породах.

Перед передней гранью перемещающегося резца создаются нормальные и касательные напряжения, приводящие к отделению породы в некотором объеме. Тогда, при бурении в направлении восстания плоскости сланцеватости, при одинаковых затратах энергии может быть отделен больший объем породы, чем при перемещении резца в направлении падения плоскости сланцеватости. Это объясняется тем, что в первом случае (рис. 11. 41, в) распространение касательных напряжений при выходе на поверхность забоя соответствует направлениям плоскостей скольжения, что позволяет оторванным элементам породы выскальзывать на поверхность без особых усилий.

Другая картина наблюдается во втором случае (рис. 11. 41, г), когда для отделения элемента породы от массива должна быть нарушена его сплошность по линии не молекулярных, а ионных или ковалентных связей, кроме того существенно затруднено удаление отделенной породы из-под передней грани, что в сумме приводит к появлению большей силы сопротивления перемещению заглубленного резца в направлении падения плоскости сланцеватости.

Этот процесс может быть рассмотрен и с позиций разных конфигураций трещин предразрушения при движении резца. При этом характер ветвления трещин, видимо, может быть различным. Можно предположить, что трещина предразрушения будет наиболее интенсивно развиваться в направлении наименьшей прочности породы, т. е. в направлении плоскостей скольжения. В таком случае наиболее предрасположенными к отделению будут зоны с проработанными зеркалами скольжения при движении резца в направлении восстания плоскости сланцеватости (рис. 11. 42, д), нежели в противоположном направлении (рис. 11. 42, е).

Естественное искривление скважин, наряду с другими причинами, происходит из-за избирательного фрезерования стенки скважины подрезными элементами и асимметричного разрушения ее забоя по площади и по глубине. Независимо от того, за счет каких причин или факторов происходит искривление, оно обусловливается наличием поперечной относительно длинной оси снаряда силы, которая стремится отклонить скважину от заданного направления. Если поперечная сила - равнодействующая множества других отклоняющих сил - отсутствует, то скважина не искривляется.

Если поперечная сила присутствует и скважина искривляется, то алмазная коронка (рис. 11. 42, а) прижимается к стенке скважины половиной своей наружной боковой поверхности, а половиной своей внутренней боковой поверхности прижимается к поверхности керна, контактируя с ними своими соответственно наружными и внутренними подрезными алмазами.

При этом результирующая внешних сил N формирует нормальную составляющую N_н на наружной боковой поверхности матрицы и аналогичную составляющую N_в на ее внутренней поверхности. При вращении коронки в направлении w появляются тангенциальные силы на наружной t_н и внутренней t_в поверхностях матрицы, действующие со стороны породы на коронку в направлении, противоположном вектору скорости.

Таким образом, на наружной боковой поверхности матрицы появляется равнодействующая R_н нормальных и тангенциальных сил, приложенных к коронке и отклоняющих коронку в левую сторону от направления действия результирующей внешних сил N. На внутренней поверхности матрицы появляется соответствующая сила R_в, отклоняющая коронку в правую сторону от направления силы N.

В том случае, когда обе поверхности матрицы несут одинаковую нагрузку, суммарная равнодействующая поперечных сил R направлена по оси действия отклоняющей силы N. При этом уход скважины в сторону от этого направления отсутствует. Если какая-то из боковых поверхностей матрицы нагружена больше другой, то вектор силы R разворачивается в соответствующую сторону, а именно: если перегружена внешняя сторона матрицы, то влево (рис. 11. 42, б), а если перегружена внутренняя сторона, то вправо (рис. 11. 42, в).

Здесь следует подчеркнуть, что направление искусственного искривления следует рассматривать в пространстве относительно вектора суммарной отклоняющей силы N. Так, если скважина естественно выполаживается равно загруженной алмазной коронкой, то при перегрузке внешней поверхности следует ожидать левого искривления. Если выполаживающаяся скважина искривляется естественно вправо, то перегрузка внешней поверхности снижает интенсивность правого искривления или при определенных условиях приводит к левому искривлению. Если же скважина выкручивается, то картина азимутального искривления будет обратной. Например, при повышении загрузки наружной поверхности коронки будет возрастать правая компонента искривления, и уменьшаться левая.

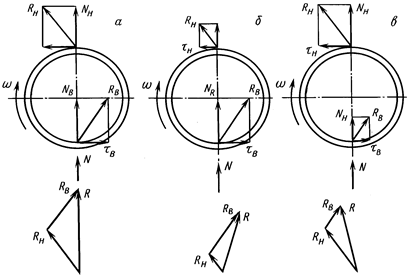
Рис. 11. 42. Упрощенные схемы поперечных отклоняющих усилий и возможные направления искривления скважин

Величина нормальной силы N на боковой поверхности матрицы коронки пропорциональна количеству установленных на ней подрезных алмазов, поскольку все они воспринимают одинаковую нагрузку. А величина силы τ, которая фактически является силой трения, равна произведению нормальной силы на коэффициент трения. Коэффициент трения, который более правильно называть коэффициентом сопротивления перемещению резца при микрорезании, очень сильно зависит от формы алмаза и параметров режима бурения.

Эти эффекты можно использовать для управления искривлением скважин, применяя коронки с заранее заданными параметрами боковых поверхностей

Закономерности естественного искривления скважин в анизотропных породах

Экспериментальный стенд и методика исследований закономерностей

искривления скважин в анизотропных породах

Для экспериментальной проверки сформулированных теоретических положений в Томском политехническом университете был создан специальный стенд.

Традиционные стенды для исследования процесса искривления скважин, например стенд А. Димитрова, стенд лаборатории бурения компании «Терра Тек Инкорпорейшн», предусматривают наличие неподвижно закрепленного образца анизотропной горной породы и относительно свободного бурового снаряда, отклоняющегося от первоначального направления при разбуривании породы. Отклонение скважины от первоначального направления или возникающие в шпинделе напряжения при нормированных условиях считаются критерием искривления скважины.

Однако при таком подходе к компоновке стенда сложно выделить в чистом виде результаты взаимодействия породоразрушающего инструмента с горной породой в связи с влиянием бурового снаряда неопределенной жесткости. Поэтому в стенде Томского политехнического института использована противоположная схема фиксации взаимодействующих элементов. Буровой снаряд зафиксирован, а образцу породы дана определенная свобода перемещения в горизонтальной плоскости в двух взаимно перпендикулярных направлениях.

Рис. 11. 43. Схема экспериментального стенда с двумя степенями свободы: 1 - коронка; 2 - шпиндель бурового станка; 3 - керн; 4 - кернодержатель; 5 ‑ платформа поперечных перемещений; 6 - опорные подшипники поперечных перемещений; 7 - платформа продольных перемещений; 8 - основание; 9 - опорные подшипники продольных перемещений; 10 - направляющие подшипники; 11 - фиксатор подвижных платформ; 12 - упругие элементы; 13 ‑ датчики перемещений

Экспериментальный стенд (рис. 11. 43) включает основание 8, на котором на подшипниках 6, 9 установлены верхняя 5 и нижняя 7 подвижные платформы, имеющие возможность перемещаться в горизонтальной плоскости. Вращению платформы препятствуют направляющие подшипники 10. На верхней платформе закреплен кернодержатель 4 с зажимными плашками. Возможность свободного перемещения платформ ограничена упругими элементами 12. Около упругих элементов смонтированы индуктивные датчики 13. Неподвижность платформ при забуривании обеспечивается фиксатором 11.

Экспериментальный стенд включает буровой станок СКБ-2, промывочный насос НБ-11Э и два самопишущих милливольтметра КСП-4.

Для измерения в процессе бурения зенитной и азимутальной составляющих сил смещения образца породы в качестве воспринимающего эти силы элемента используют упругие стальные пластины. Передача силы смещения на пластины соответствующих кареток осуществляется через шарнирные упоры, закрепленные в верхних частях пластин. Величина изгиба пластины соответствует величине приложенной смещающей силы и измеряется индуктивными датчиками, тарированными в единицах силы.

Методика экспериментального бурения заключалась в следующем. В кернодержателе закреплялся керн анизотропной горной породы, имеющий параллельную сланцеватость. Плоскость сланцеватости устанавливалась под требуемым углом к оси шпинделя станка. При застопоренных с помощью фиксатора платформах забуривалась скважина на высоту матрицы коронки. Затем при выключенной подаче проводилась приработка алмазной коронки, необходимая для снятия напряжений в шпинделе, возникших при забуривании.

После окончания приработки коронки без остановки вращения платформы расстопаривались, включалась подача шпинделя при сохранении режима промывки, включались электросекундомер и самописцы, фиксировались значения поперечных сил при установленных параметрах режима бурения. В зависимости от условий эксперимента углубка проводилась либо ступенчато, либо непрерывно на всю высоту образца. Эксперимент считался состоявшимся в том случае, когда на диаграмме наблюдалась зона устойчивого режима, т. е. сила упругой деформации пластинчатой пружины уравновешивала поперечную отклоняющую силу, генерируемую на контакте резцов коронки и горной породы.

Наличие этого экспериментального стенда позволило впервые выделить в чистом виде и разложить на поперечные составляющие силы, возникающие на контакте алмазной коронки и анизотропной горной породы, которые приводят к отклонению бурового снаряда от прямолинейной траектории.

Связь поперечных отклоняющих сил с осевой нагрузкой на породоразрушающий инструмент и частотой оборотов бурового снаряда

Экспериментальные исследования отклоняющих сил осуществлялись в двух взаимно перпендикулярных направлениях в горизонтальной плоскости. Одно из этих направлений соответствовало проекции линии падения плоскости сланцеватости. Сила, действующая в этом направлении, названа зенитной (P_q). Если сила направлена в сторону восстания плоскости сланцеватости, то она считается положительной, а если в сторону падения этой плоскости - отрицательной.

Другая сила, соответствующая проекции линии простирания плоскости сланцеватости, названа азимутальной (P_a). Если сила, отклоняющая снаряд, направлена вправо от проекции линии восстания плоскости сланцеватости, то она считается положительной, а если влево - отрицательной.

Экспериментальные исследования осуществлялись на рассланцованных породах Таштагольской серии VI-IХ категории по буримости при углах встречи 45° c плоскостью сланцеватости тремя однослойными алмазными коронками диаметром 36 мм. Основные результаты экспериментов приведены в табл. 11. 4.

Таблица 11. 4.

Результаты экспериментального бурения

Номер коронки	z	n = 325 мин^-1			n = 645 мин^-1			, даН	, даН
Номер коронки	z	C₀_y, МПа	P_q, даН	P_a, даН	C₀_y, МПа	P_q, даН	P_a, даН	, даН	, даН
	0, 50	2, 6 4, 9 7, 0	4, 92 7, 96 12, 07	1, 15 2, 08 -0, 20	2, 6 3, 5 5, 1	2, 35 5, 82 8, 04	2, 13 1, 20 1, 09	7, 15	1, 53
	0, 35	2, 6 4, 9 7, 0	3, 68 5, 14 6, 07	0, 21 1, 54 -0, 93	2, 6 3, 5 5, 1 7, 0	2, 37 3, 90 7, 08 5, 65	2, 13 0, 60 -0, 38 -5, 80	5, 06	0, 38
	0, 15	2, 6 4, 9 7, 0	4, 71 6, 13 12, 81	0, 77 -0, 06 -3, 69	2, 6 3, 5 5, 1	4, 22 3, 32 8, 45	0, 98 1, 72 -0, 68	7, 10	-0, 59

Примечание. z - отношение количества алмазов на внутренней и наружной поверхностях матрицы; C₀_y - удельная осевая нагрузка; n - частота вращения.

Зависимости зенитной силы от удельной осевой нагрузки при разных частотах вращения, построенные на основании табл. 11. 4., приведены на рис. 11. 44.

Анализ кривых (рис. 11. 44) позволяет сделать следующие выводы:

1. Отклоняющая сила, формирующая зенитное искривление, имеет абсолютную величину от 2 до 13 даН.

2. Как правило, зенитная отклоняющая сила возрастает с увеличением осевой нагрузки.

3. При малых частотах оборотов эта зависимость хорошо аппроксимируется уравнением прямой линии.

4. При возрастании частоты оборотов эта зависимость менее выражена, хотя в целом тенденция сохраняется.

5. Связь зенитной силы с частотой оборотов при проведении данных экспериментов не столь однозначна, как с осевой нагрузкой.

6. При частоте вращения 645 мин^-1 и малых удельных нагрузках 2-3 МПа зенитная сила меньше, чем при таких же нагрузках, но меньших частотах вращения.

7. При частоте вращения 645 мин^-1 и больших удельных нагрузках 4-7 МПа зенитная сила имеет большие значения, чем при малых частотах оборотов.

Рис. 11. 44. Зависимость величины зенитного отклоняющего усилия от удельной осевой нагрузки для алмазных коронок № 34 (а), № 135 (б), № 153 (в) диаметром 36 мм при различных частотах вращения n, мин^-1: 1, 2 - 325; 3, 4 - 645; 1, 3 - эмпирические кривые; 2, 4 - теоретические прямые

Таблица 11. 5.

Корреляционные характеристики распределения зенитных сил

Номер коронки	n, мин^-1	P_q=f(C₀_y), даН	N, шт	r	t	t_{v; 0, 05}
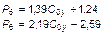
				0, 496 0, 745	3, 18 5, 12	2, 04 2, 07
				0, 335 0, 564	2, 11 2, 84	2, 03 2, 11
				0, 735 0, 455	6, 30 2, 23	2, 03 2, 09

В табл. 11. 5 приведены корреляционные характеристики распределения зенитных сил, определяющие форму их связи с удельной осевой нагрузкой, степень связи этих параметров (r - коэффициент парной корреляции) и оценки степени связи параметров (t - расчетная статистика и t_v_{; 0, 05} - табличная статистика при и уровне значимости 0, 05). Поскольку все t - расчетные больше t - табулированных, зависимости зенитной силы от осевой нагрузки надежно описываются уравнениями прямых линий.

При анализе закономерностей формирования азимутальной силы необходимо учитывать, что для экспериментов были выбраны алмазные коронки, имеющие разное вооружение наружной и внутренней боковых поверхностей матрицы. Коронка № 34 имела соотношение количества внутренних и наружных подрезных алмазов, равное 0, 5; № 135 имела это соотношение 0, 35 и № 53 - соответственно 0, 15. Для определения названного соотношения боковые поверхности матриц стандартных алмазных коронок были обработаны электрохимическим способом, и обнаженные алмазы пересчитаны под микроскопом.

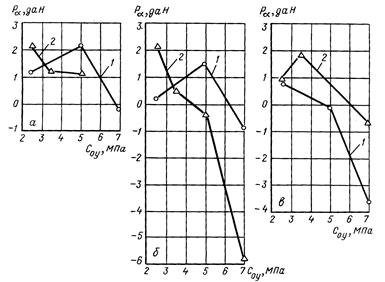
Рис. 11. 45. Зависимости величины азимутальной отклоняющей силы от удельной осевой нагрузки для алмазных коронок № 34 (а), № 135 (б), № 153 (в) диаметром 36 мм при разных частотах вращения n, мин^-1: 1 - 325; 2 - 645

Информация, приведенная на рис. 11. 45, позволяет сделать важные выводы о закономерностях азимутального искривления скважин.

1. Характер азимутальной силы очень существенно зависит от соотношения числа внутренних и наружных подрезных алмазов. При соотношении, равном 0, 5, зафиксировано положительная азимутальная сила, равная 1, 53 даН. При уменьшении соотношения алмазов до 0, 35 сила остается положительной, но ее значение уменьшается до 0, 38 даН. Наконец, при величине соотношения 0, 13 преобладающей в азимутальном искривлении становится левая компонента, а сила равна -0, 59 даН.

2. Очень активную роль при формировании азимутальной силы играет осевая нагрузка. Для всех коронок с ростом нагрузки уменьшается правая компонента и увеличивается левая. Переход от правого искривления к левому не достигнут только у коронки № 34 с соотношением алмазов 0, 5 при частоте оборотов 645 мин^-1. В пяти остальных группах экспериментов при начальной удельной нагрузке 2, 6 МПа наблюдалось положительная сила (правое искривление), а при максимальном давлении 4, 9-7 МПа - отрицательная (левое искривление).

3. Частота оборотов не столь существенно влияет на азимутальное отклонение, однако, в целом, просматривается увеличение правой компоненты искривления с ростом частоты оборотов.

Все изложенное позволило предположить, что отклоняющие зенитная и азимутальная силы связаны между собой. Результаты корреляционного анализа связей между ними сведены в табл. 11. 6.

Таблица 11. 6.

Результаты корреляционного анализа связей между зенитным P_q
и азимутальным P_a усилиями

Номер коронки	n, мин^-1	r	Уравнение связи	, даН	, даН	N, шт
		-0, 45 -0, 39		1, 8 1, 4	8, 0 6, 1
		-0, 14 -0, 54		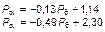0, 5 -0, 1	4, 8 4, 8
		-0, 32 -0, 12		-1, 0 0, 1	7, 6 6, 2

Для прогнозирования азимутального усилия по материалам экспериментального бурения рассчитано уравнение множественной корреляции, связывающее величину азимутального усилия с параметрами режима бурения

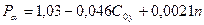. (11. 43)

Между зенитной и азимутальной силами во всех случаях существует обратная зависимость. Это позволяет сделать определенные выводы относительно природы азимутального искривления скважин и создать систему мер по его регулированию.

Обратимся к рис. 11. 40. Торцевые алмазы коронки в точке А движутся вслед плоскости сланцеватости, а в точке В – навстречу. На мой взгляд, это приводит к асимметричному разрушению забоя по глубине. То есть в точке А скорость бурения выше, чем в диаметрально противоположной точке. Таким образом, в результате этого скважина должна двигаться по правому винту, то есть выполаживаться и поворачиваться вправо по азимуту.

А теперь посмотрим рис. 11. 42. Поскольку алмазная коронка на внутренней поверхности всегда имеет меньшее количество подрезных алмазов, чем на наружной, то поперечные нормальные и тангенциальные силы на наружной поверхности больше, чем на внутренней. Поэтому, если принимать в расчет только поперечные компоненты, скважина должна искривляться по левому винту, то есть выполаживаться и отклоняться влево по азимуту за счет ассиметричного разрушения забоя по плоскости. Но эти поперечные компоненты начинают превалировать в том случае, когда поперечная сила достаточна велика, то есть велика сила, прижимающая боковые поверхности матрицы к стенке скважины и керна.

Таким образом, при малых осевых нагрузках создается малая зенитная отклоняющая сила, поэтому скважина искривляется в основном по азимуту вправо за счет асимметричного разрушения забоя по глубине в точках А и В (рис. 11. 40). При наращивании осевой нагрузки увеличивается зенитная сила, возрастают нормальные и тангенциальные силы на боковых поверхностях матрицы коронки, и начинают проявляться поперечные компоненты (рис. 11. 42). Это приводит сначала к снижению интенсивности правого искривления, а затем – к изменению направления азимутального искривления на противоположное (левое).

Роль промывочной жидкости при искривлении скважин
в анизотропных породах

Существует мнение о том, что роль промывочной жидкости в закономерностях искривления скважин определяется ее способностью сохранять или увеличивать диаметр скважины. В частности, имеются утверждения о том, что увеличение расхода промывочной жидкости приводит к существенному расширению скважины в призабойной зоне, сопровождаемому дополнительным перекосом колонкового набора и повышением интенсивности искривления. Однако исследования, проведенные Ф. А. Вайновым и Ю. С. Ивановым, показали, что каждая скважина, пробуренная в скальных и полускальных породах, имеет в призабойной зоне интервал устойчивости, длина которого всегда больше 7-10 м. Диаметр скважины в этом интервале почти равен диаметру породоразрушающего инструмента. Следовательно колонковый набор всегда работает в скважине одного диаметра Поэтому тезис о влиянии размыва стенок скважины на интенсивность искривления может быть снят. Тем не менее, режим промывки оказывает существенное влияние на искривление скважин.

Выдвинутое предположение о приоритетном характере влияния сил сопротивления породы поперечному перемещению резца при бурении в анизотропных породах на искривление скважин потребовало экспериментальной проверки закономерностей искривления скважин при промывке разными жидкостями.

Исследованиями П. А. Ребиндера и др. установлено, что в процессе бурения непосредственно под коронкой образуется трещиноватая зона, и циркулирующая жидкость со смачивающим агентом проникает в микротрещины этой зоны. Использование промывочной жидкости с увеличенной смачивающей способностью повышает эффективность разрушения породы вследствие проникновения смачивателя в микротрещины и адсорбирования его на поверхностях. Этот эффект может активизироваться при бурении в анизотропных породах, склонных к образованию многочисленных плоскостей скольжения, сообщающихся с поверхностью забоя.

В связи с этим был проведен ряд циклов экспериментального бурения рассланцованных горных пород при промывке водным однопроцентным раствором сульфонола, являющегося активным понизителем твердости, и проведено сравнение величин отклоняющих зенитных и азимутальных сил с соответствующими результатами, полученными при промывке скважин технической водой. Основные результаты приведены в табл. 11. 7..

Таблица 11. 7.

Сравнительные результаты экспериментального бурения скважин в анизотропных породах алмазными коронками диаметром 36 мм при промывке жидкостями разного типа

Параметры	Тип промывочной жидкости:
Параметры	вода	1%-ный раствор сульфонола
Число циклов
С₀_y, МПа	5, 3	5, 3
n, мин^-1
Р_q, даН	8, 61	3, 81
Р_a, даН	- 0, 72	0, 78
v_м, мм/с	0, 68	0, 76

Зенитная сила уменьшилась более чем в 2 раза, что, в свою очередь, изменило характер азимутальной силы. Поскольку при бурении с промывкой водой зенитная сила большое, существенно проявилась левая компонента искривления (поперечные эффекты), что подтверждает сделанные ранее выводы.

Исследование характера влияния промывочной жидкости на искривление скважин должно стать объектом серьезных исследований, успешное выполнение которых должно открыть новые возможности управления процессом направленного бурения.

Расчет интенсивности искривления скважин

в анизотропных породах

Из-за разницы сопротивления породы разрушению в разных точках забоя возникает отклоняющая сила DF_т, что приводит к смещению породоразрушающего инструмента в направлении восстания плоскости сланцеватости. Знание величины этой силы или наличие экспериментальной базы для ее определения позволяет рассчитать проектную предельную интенсивность естественного искривления любой конкретной скважины.

Для решения этой задачи необходимо иметь образцы горных пород, соответствующие условиям бурения проектных скважин, и методику расчета проектной интенсивности искривления. На поздних стадиях разведки месторождений полезных ископаемых при сгущении разведочной сети, когда требования к качеству разведки наиболее высоки, образцы горных пород могут быть изготовлены из кернов уже пробуренных скважин.

Рис. 11. 46. Схема к расчету интенсивности искривления скважин в анизотропных породах

Методика расчета проектной интенсивности естественного искривления разработана на основании классических приемов теории сопротивления материалов. Она основывается на том, что в анизотропных породах за счет действия поперечной силы DF_т и других сил скважина резко отклоняется от первоначального прямолинейного направления. В определенный момент времени при достижении предела вписываемости снаряд касается стенок скважины и забоя в трех точках А, В, С (рис. 11. 46). При дальнейшем искривлении скважины появляется поперечный изгиб снаряда за счет действия породы на колонковую трубу в точке В с силой Р, которая пропорциональна прогибу трубы y_к. За счет упругости колонкового набора сила Р передается в точке А и С и воздействует на стенку скважины. Причем величина силы в точках А и С равна половине силы Р.

Сила возрастает с увеличением интенсивности искривления скважины и изгибом колонковой трубы по законам механики, в то время как величина смещающей силы DF_т остается постоянной для данных геолого-технических условий.

В тот момент, когда возрастает до такой степени, что сравняется с отклоняющей силой DF_т, искривление скважины должно стабилизироваться. При этом колонковая труба вращается вокруг криволинейной оси. Другие виды движения практически исключаются, поскольку снаряд зажат в резко искривленном призабойном участке.

Сила Р может быть легко рассчитана, исходя из упругих свойств колонковой трубы,

, (11. 44)

где y_к - величина наибольшего прогиба трубы; Е - модуль упругости; I - момент инерции сечения трубы; l - длина колонковой трубы.

Радиус искривления скважины

, (11. 45)

где y_с - наибольший прогиб скважины на отрезке, равном l.

Выразим прогиб оси скважины через величину прогиба оси трубы,

, (11. 46)

где y - угол смежности точек В и С; Dr - радиальный зазор между колонковой трубой и скважиной.

Поскольку y в реальных условиях не превышает нескольких градусов, запишем

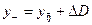, (11. 47)

где DD - диаметральный зазор между колонковой трубой и скважиной.

Решаем уравнение (11. 44) относительно y_к, приравнивая DF_т к Р/2.

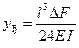, (11. 48)

Подставим выражение (11. 46) в равенство (11. 45) и решим относительно y_к.

. (11. 49)

Приравняем правые части уравнений (11. 48) и (11. 49) и решим относительно R_с.

. (11. 50)

Далее несложно определить интенсивность естественного искривления скважин.

, (11. 51)

где DD - диаметральный зазор, м; DF_т - отклоняющая сила, даН; l - длина колонковой трубы, м; Е - модуль Юнга, даН/м²; I - момент инерции сечения трубы, м⁴.

Вид последнего уравнения позволяет сделать вывод о возможном наличии экстремума длины колонковой трубы, обеспечивающей минимальную интенсивность искривления. Для отыскания экстремума продифференцируем уравнение (11. 51) относительно длины, приравняем первую производную нулю и решим полученное уравнение относительно длины.

; (11. 52)

, (11. 53)

где l₀ - длина колонковой трубы, обеспечивающая минимальную интенсивность искривления.

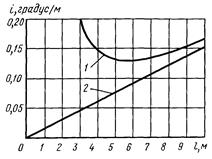
Проиллюстрируем графически экстремальный характер уравнения (11. 51), проведя расчеты интенсивности искривления для колонковых труб диаметром 73 мм и дезориентирующей силы 10 даН (рис. 11. 47).

Рис. 11. 47. Зависимость интенсивности искривления скважин от длины колонкового набора диаметром 73 мм при отклоняющей силе 10 даН: 1 ‑ стандартный колонковый набор; 2 - сцентрированный в скважине колонковый набор

Трансформируем уравнение (11. 51) для полностью сцентрированной в скважине колонковой трубы, приравняв нулю диаметральный зазор, получим уравнение

. (11. 54)

Решим его для тех же усилий, что и предыдущее, и полученную линейную зависимость интенсивности искривления от длины трубы приведем также на рис. 2. 13.

Таблица 11. 8

Интенсивность искривлен

⇐ Предыдущая 2 3 4 5 6 7 8 91011 Следующая ⇒

Воспользуйтесь поиском по сайту: