 |
Парная регрессия и корреляция
|
|
|
|
Министерство образования и науки РФ
Южно-Российский государственный университет экономики и сервиса 
Безуглова Н.П.
Фетисов В.Г.
Эконометрика
Практическое пособие
ШАХТЫ 2004
УДК 519.862.6 (07)
ББК 65в6(Я7)
Б 406
Авторы:
ассистент кафедры «Математика»
Н.П.Безуглова,
д.ф.-м.н., профессор кафедры «Математика»
В.Г.Фетисов
Рецензенты:
д.т.н, профессор кафедры РЭС
К.Е.Румянцев
к.ф.-м.н., доцент кафедры «Математика»
В.И.Филиппенко
Б 406 Безуглова Н.П.. Эконометрика: Практическое пособие/ Н.П.Безуглова, В.Г.Фетисов. – Изд-во ЮРГУЭС, 2004.- 52с.
Данное практическое пособие содержит краткие теоретические сведения, примеры решения типовых задач, а также контрольные вопросы и упражнения по основным разделам учебной дисциплины «Эконометрика». Пособие предназначено для студентов, обучающихся по специальностям 060400 «Финансы и кредит» и 060500 «Бухгалтерский учет и аудит» дневной и заочной форм обучения.
©Южно-Российский государственный
университет экономики и сервиса,2004
©Безуглова Н.П., Фетисов В.Г., 2004
Содержание
| 1 ПРЕДМЕТ, ЗАДАЧИ И МЕТОДЫ ЭКОНОМЕТРИКИ | |
| 2 Парная регрессия и корреляция | |
| 2.1 Краткая теория | |
| 2.2 Примеры решения задач | |
| 3 множественная регрессия и корреляция | |
| 3.1 Краткая теория | |
| 3.2 Примеры решения задач | |
| 4 система линейных эконометрических уравнений | |
| 4.1 Краткая теория | |
| 4.2 Примеры решения задач | |
| 5 ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ | |
| 4.1 Краткая теория | |
| 4.2 Примеры решения задач | |
| 6 КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ | |
| Библиографический список |
1 ПРЕДМЕТ, ЗАДАЧИ И МЕТОДЫ ЭКОНОМЕТРИКИ
|
|
|
Создание надежной информационной базы для менеджмента во всех отраслях экономики невозможно без учёта действия различных факторов, формирующих результаты работы организаций (предприятий). Необходимо выделить роль факторов, которые положительно или отрицательно влияют на результаты хозяйствования. Одновременно целесообразно выделить отдельно влияние факторов, которые зависят непосредственно от принятия управленческих решений данным объектом хозяйствования (предприятием, фирмой, ассоциацией предприятий или регионом) и влияние факторов, которые от менеджмента на данном хозяйственном объекте не зависят. При отсутствии необходимых для переходного периода к рыночной экономике законов или при изменении цен, тарифов, экономических нормативов, налогов, инфляции, которые, несомненно, от конкретного объекта хозяйствования не зависят, ухудшаются экономические результаты его работы. Устранение влияния таких факторов в эконометрических расчетах и характеристика их влияния путем соответствующих вычислений позволяет более правильно прогнозировать результаты хозяйственной деятельности в будущем периоде.
Эконометрические расчеты помогают лучше понять хозяйственные явления и процессы, что в свою очередь позволяет более достоверно формулировать советы и давать прогнозы.
Предметом эконометрики являются факторы, формирующие развитие экономических явлений и процессов. Эконометрика-это искусство разработки и предвидения экономических нормативов, прогнозов и гипотез.
Основными задачами эконометрики являются: оценка направленных действий специалистов на достижение экономической эффективности хозяйственной деятельности; прогнозирование путей развития макро- и микроэкономических факторов хозяйственной деятельности. Прогнозная информация должна давать возможность принимать решение в зависимости от хозяйственной коньюктуры. Успешное выполнение поставленных перед эконометрикой задач зависит от соблюдения всех критериев и принципов эконометрических расчетов от формулировки проблемы, отбора цели, составления альтернативных действий, сбора данных, выбора метода их оценки и построения экономических прогнозов или моделей, взвешивания затрат по отношению к экономическим результатам, дополнительной проверки предпосылок и исходных данных до улучшения модели.
|
|
|
Наибольшее распространение в практике эконометрики имеет метод регрессионного и корреляционного анализа. Для успешного применения этого метода необходимо соблюдать статистические критерии для обработки информации о хозяйственной деятельности: наличие многочисленной совокупности предприятий, случайности хозяйственных и экономических процессов, одинаковых единиц измерения факторов и результативных показателей, нормального распределения переменных; отсутствие функциональной связи между факторами и т.д.
Парная регрессия и корреляция
Краткая теория
Парная регрессия – уравнение связи двух переменных
 ,
,
где 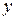 - зависимая переменная (результативный признак),
- зависимая переменная (результативный признак),
 - независимая, объясняющая переменная (фактор-признак).
- независимая, объясняющая переменная (фактор-признак).
Различают линейные и нелинейные регрессии.
Линейная регрессия:  .
.
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
· полиномы разных степеней 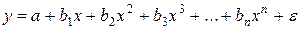 ;
;
· равносторонняя гипербола  .
.
Регрессии, нелинейные по оцениваемым параметрам:
· степенная  ;
;
· показательная 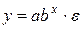 ;
;
· экспоненциальная 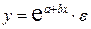
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака 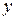 от теоретических
от теоретических  минимальна, т.е.
минимальна, т.е.
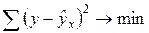 .
.
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно  и
и  .
.
|
|
|
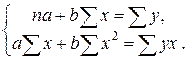
Можно воспользоваться готовыми формулами, вытекающими из этой системы:
 ,
,
 .
.
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции 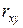 для линейной регрессии (
для линейной регрессии (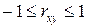 ):
):
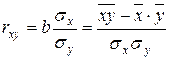 ,
,
и индекс корреляции  - для нелинейной регрессии (
- для нелинейной регрессии (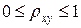 ):
):
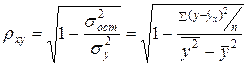 .
.
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
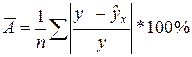 .
.
Допустимый предел значений  - не более 8-10%.
- не более 8-10%.
Средний коэффициент эластичности 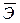 оценивает силу влиянии фактора на результат и показывает, на сколько процентов в среднем по совокупности изменится результат
оценивает силу влиянии фактора на результат и показывает, на сколько процентов в среднем по совокупности изменится результат 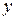 от своей средней величины при изменении фактора
от своей средней величины при изменении фактора  на 1% от своего среднего значения:
на 1% от своего среднего значения:
 .
.
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
 ,
,
где  - общая сумма квадратов отклонений;
- общая сумма квадратов отклонений;
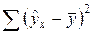 - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
- сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
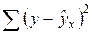 - остаточная сумма квадратов отклонений.
- остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака 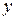 характеризует коэффициент (индекс) детерминации -квадрат коэффициента или индекса корреляции.
характеризует коэффициент (индекс) детерминации -квадрат коэффициента или индекса корреляции.
F-тест – оценивание качества уравнения регрессии состоит в проверке гипотезы  о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического
о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического  и критического (табличного)
и критического (табличного)  значений F-критерия Фишера.
значений F-критерия Фишера.  определяется из соотношения факторной и остаточной дисперсий, рассчитанный на одну степень свободы:
определяется из соотношения факторной и остаточной дисперсий, рассчитанный на одну степень свободы:
 ,
,
где 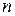 -число единиц совокупности (наблюдений),
-число единиц совокупности (наблюдений),  -число параметров при переменных
-число параметров при переменных  в уравнении регрессии.
в уравнении регрессии.
 - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости
- это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости  -вероятности отвергнуть нулевую гипотезу
-вероятности отвергнуть нулевую гипотезу  при условии, что она верна.
при условии, что она верна.  обычно принимается равным 0,05 или 0,01.
обычно принимается равным 0,05 или 0,01.  определяется по таблице и зависит от уровня значимости, числа степеней свободы
определяется по таблице и зависит от уровня значимости, числа степеней свободы  и числа степеней свободы
и числа степеней свободы  . Таблицу для определения
. Таблицу для определения  а так же таблицы других используемых при решении задач статистик можно найти в [1].
а так же таблицы других используемых при решении задач статистик можно найти в [1].
|
|
|
Если  , то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. В противном случае гипотеза
, то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. В противном случае гипотеза  не отклоняется и признается статистическая незначимость, ненадёжность уравнения регрессии и показателя тесноты связи.
не отклоняется и признается статистическая незначимость, ненадёжность уравнения регрессии и показателя тесноты связи.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывается t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза  о случайной природе показателей, т.е. незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия проводится путем сопоставления их значений с величиной случайной ошибки.
о случайной природе показателей, т.е. незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия проводится путем сопоставления их значений с величиной случайной ошибки.
Случайные ошибки показателей 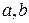 и
и 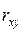 определяются по формулам:
определяются по формулам:
 ,
,
 ,
,
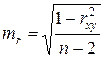 .
.
Фактическиезначения t-критерия вычисляются следующим образом:
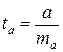 ,
,
 ,
,
 .
.
Критическое значение t-критерия 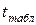 определяется по таблице и зависит от уровню значимости
определяется по таблице и зависит от уровню значимости  и числа степеней свободы
и числа степеней свободы  , где
, где 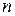 -число единиц совокупности (наблюдений).
-число единиц совокупности (наблюдений).
Если  , то гипотеза
, то гипотеза  о случайной природе показателей отклоняется, т.е.
о случайной природе показателей отклоняется, т.е.  ,
,  и
и 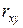 не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора
не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора  . В противном случае гипотеза
. В противном случае гипотеза  принимается и признается случайная природа формирования показателей
принимается и признается случайная природа формирования показателей  ,
,  и
и 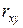 .
.
Для расчета доверительных интервалов определяем предельную ошибку  для каждого из показателей:
для каждого из показателей:
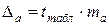 ,
,
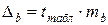 .
.
Доверительные интервалы рассчитываются по формулам:
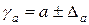 ,
,
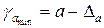 ,
,
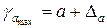 ;
;
 ,
,
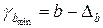 ,
,
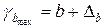 .
.
Если в границы доверительного интервала попадает нуль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр признается нулевым, статистически ненадёжным, так как он не может одновременно принимать и положительные и отрицательные значения.
Прогнозное значение 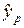 определяется путем подстановки в уравнение регрессии
определяется путем подстановки в уравнение регрессии  соответствующего (прогнозного) значения
соответствующего (прогнозного) значения 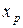 . Вычисляется средняя стандартная ошибка прогноза
. Вычисляется средняя стандартная ошибка прогноза 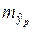 :
:
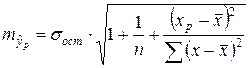 ,
,
где 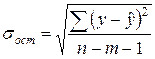 ;
;
и строится доверительный интервал прогноза:
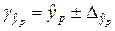 ,
,
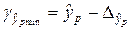 ,
,
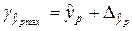 ,
,
где 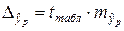 .
.
Примеры решения задач
Пример 2.2.1
По 12 территориям России за 199Х г. известны значения двух признаков (табл. 2.2.1.)
Таблица 2.2.1
| Район | Средняя заработная плата работающего, тыс. руб., x | Доля денежных средств, направляемых на прирост сбережений во вкладах, %, y |
| Респ. Карелия | 2,01 | |
| Архангельская обл. | 2,83 | |
| Вологодская обл. | 3,46 | |
| Новгородская обл. | 3,99 | |
| Ростовская обл. | 4,47 | |
| Орловская обл. | 4,89 | |
| Ярославская обл. | 5,29 | |
| Калужская обл. | 5,65 | |
| Ленинградская обл. | 6,01 | |
| Мурманская обл. | 6,32 | |
| Респ. Коми | 6,63 | |
| Московская. обл. | 6,92 |
Требуется:
|
|
|
1. Для характеристики зависимости 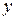 от
от  рассчитать параметры следующих функций: А) линейной; Б) степенной; В) показательной; Г) равносторонней гиперболы.
рассчитать параметры следующих функций: А) линейной; Б) степенной; В) показательной; Г) равносторонней гиперболы.
2. Оценить каждую модель через среднюю ошибку аппроксимации, показатель корреляции и F-критерий Фишера. Выбрать лучшую модель.
Решение.
А) Для расчета параметров  и
и  линейной регрессии
линейной регрессии  составим следующую таблицу (табл.2.2.2.)
составим следующую таблицу (табл.2.2.2.)
Таблица 2.2.2
| Район | 
| 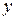
| 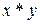
| 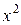
| 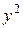
| 
| 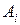
|
| Респ. Карелия | 2,01 | 2,01 | 4,0401 | 2,521154 | 25,4305 | ||
| Архангельская обл. | 2,83 | 5,66 | 8,0089 | 2,948671 | 4,19333 | ||
| Вологодская обл. | 3,46 | 10,38 | 11,9716 | 3,376189 | 2,42229 | ||
| Новгородская обл. | 3,99 | 15,96 | 15,9201 | 3,803706 | 4,66902 | ||
| Ростовская обл. | 4,47 | 22,35 | 19,9809 | 4,231224 | 5,34175 | ||
| Орловская обл. | 4,89 | 29,34 | 23,9121 | 4,658741 | 4,72922 | ||
| Ярославская обл. | 5,29 | 37,03 | 27,9841 | 5,086259 | 3,85144 | ||
| Калужская обл. | 5,65 | 45,2 | 31,9225 | 5,513776 | 2,41104 | ||
| Ленинградская обл. | 6,01 | 54,09 | 36,1201 | 5,941294 | 1,1432 | ||
| Мурманская обл. | 6,32 | 63,2 | 39,9424 | 6,368811 | 0,77233 | ||
| Респ. Коми | 6,63 | 72,93 | 43,9569 | 6,796329 | 2,50873 | ||
| Московская обл. | 6,92 | 83,04 | 47,8864 | 7,223846 | 4,39084 | ||
| ИТОГО | 58,47 | 441,19 | 311,646 | 61,8637 | |||
| Среднее | 6,5 | 4,8725 | 36,7658 | 54,167 | 25,9705 | 5,15531 | |
| Дисперсия | 11,9167 | 2,2293 | |||||
| Ср.кв.отклонение | 3,4521 | 1,4931 |
Напомним, что средние значения рассчитываются по формулам 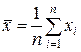 ,
,  ,
,  ,
,  и т.д., где
и т.д., где 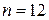 (число наблюдений в рассматриваемой задаче). Дисперсия определяется по формулам
(число наблюдений в рассматриваемой задаче). Дисперсия определяется по формулам  ,
,  , а среднеквадратическое отклонение есть корень квадратный из дисперсии.
, а среднеквадратическое отклонение есть корень квадратный из дисперсии.
Рассчитаем параметры  и
и  линейной регрессии
линейной регрессии  .
.
 ,
,
 .
.
Уравнение линейной регрессии имеет вид 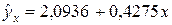 .
.
Рассчитаем линейный коэффициент парной корреляции
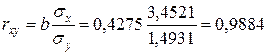 . Связь сильная (так как
. Связь сильная (так как 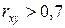 ), прямая (так как
), прямая (так как 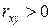 ).
).
Коэффициент детерминации  , значит, вариация результата на 97,7% объясняется вариацией фактора
, значит, вариация результата на 97,7% объясняется вариацией фактора  , а на 2,3% вариацией неучтенных в модели признаков. Подставляя в уравнение регрессии фактические значения
, а на 2,3% вариацией неучтенных в модели признаков. Подставляя в уравнение регрессии фактические значения  , определим теоретические (расчетные) значения
, определим теоретические (расчетные) значения  . Найдем величину средней ошибки аппроксимации:
. Найдем величину средней ошибки аппроксимации:
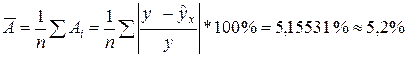 .
.
В среднем расчетные значение от фактических отклоняются на 5,2%, это говорит об удовлетворительном качестве модели, поскольку средняя ошибка аппроксимации не превышает 8-10%.
Оценим теперь статистическую надежность полученной модели с помощью F-критерия Фишера. Выдвигаем гипотезу  о статистической незначимости уравнения регрессии и показателя тесноты связи.
о статистической незначимости уравнения регрессии и показателя тесноты связи.
 .
.
Определяем по таблице значений F-критерия Фишера  . Так как
. Так как  , то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.
, то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.
Б) Построению степенной модели 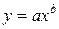 предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
 ;
;
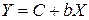 , где
, где  ,
, 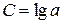 ,
,  .
.
Для расчетов используем данные таблицы 2.2.3.
Таблица 2.2.3
| Район | 
| 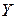
| 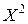
| 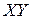
| 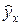
| 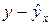
| 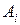
| 
|
| Респ. Карелия | 0,303 | 2,0044 | 0,0056 | 0,2778 | 0,0000311745 | |||
| Архангельская обл. | 0,301 | 0,452 | 0,091 | 0,136 | 2,8318 | -0,0018 | 0,0639 | 0,0000032712 |
| Вологодская обл. | 0,477 | 0,539 | 0,228 | 0,257 | 3,4662 | -0,0062 | 0,179 | 0,0000383477 |
| Новгородская обл. | 0,602 | 0,601 | 0,362 | 0,362 | 4,0007 | -0,0107 | 0,2691 | 0,0001152464 |
| Ростовская обл. | 0,699 | 0,65 | 0,489 | 0,455 | 4,4715 | -0,0015 | 0,0336 | 0,0000022573 |
| Орловская обл. | 0,778 | 0,689 | 0,606 | 0,536 | 4,897 | -0,007 | 0,1428 | 0,0000487626 |
| Ярославская обл. | 0,845 | 0,723 | 0,714 | 0,611 | 5,2882 | 0,0018 | 0,0348 | 0,0000033965 |
| Калужская обл. | 0,903 | 0,752 | 0,816 | 0,679 | 5,6522 | -0,0022 | 0,0385 | 0,0000047380 |
| Ленинградская обл. | 0,954 | 0,779 | 0,911 | 0,743 | 5,994 | 0,016 | 0,2661 | 0,0002557166 |
| Мурманская обл. | 0,801 | 0,801 | 6,3173 | 0,0027 | 0,0432 | 0,0000074573 | ||
| Респ. Коми | 1,041 | 0,822 | 1,084 | 0,856 | 6,6247 | 0,0053 | 0,0801 | 0,0000282301 |
| Московская. обл. | 1,079 | 0,84 | 1,165 | 0,907 | 6,9184 | 0,0016 | 0,0234 | 0,0000026192 |
| ИТОГО | 8,68 | 7,951 | 7,464 | 6,343 | 1,4523 | 0,0005412173 | ||
| Среднее | 0,723 | 0,663 | 0,622 | 0,529 | 0,121 | 0,0000451014 | ||
| Дисперсия | 0,099 | 0,025 |
Рассчитаем 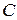 и
и  :
:
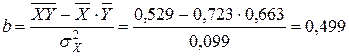 ,
,
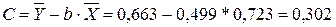 .
.
Получим линейное уравнение 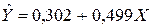 .
.
Выполнив его потенцирование, получим:
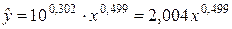 .
.
Подставляя в уравнение регрессии фактические значения  , определим теоретические (расчетные) значения
, определим теоретические (расчетные) значения  . По ним рассчитаем показатели: тесноты связи- индекс корреляции
. По ним рассчитаем показатели: тесноты связи- индекс корреляции  и среднюю ошибку аппроксимации:
и среднюю ошибку аппроксимации:
 . Связь сильная. Коэффициент детерминации
. Связь сильная. Коэффициент детерминации  , значит, вариация результата на 99,998% объясняется вариацией фактора
, значит, вариация результата на 99,998% объясняется вариацией фактора  , а на 0,002 % вариацией неучтенных в модели признаков.
, а на 0,002 % вариацией неучтенных в модели признаков.
Величина средней ошибки аппроксимации  говорит об удовлетворительном качестве модели, поскольку
говорит об удовлетворительном качестве модели, поскольку  не превышает 8-10%.
не превышает 8-10%.
Оценим теперь статистическую надежность полученной модели с помощью F-критерия Фишера. Выдвигаем гипотезу  о статистической незначимости уравнения регрессии и показателя тесноты связи.
о статистической незначимости уравнения регрессии и показателя тесноты связи.
 .
.
 .
.
Так как  , то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.
, то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.
В) Построению показательной модели 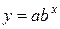 предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
 ;
;
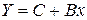 , где
, где  ,
,  ,
, 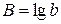 .
.
Для расчетов используем данные таблицы 2.2.4.
Таблица 2.2.4
| Район | 
| 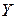
| 
| 
| 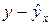
| 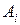
| 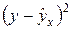
|
| Респ. Карелия | 0,303 | 0,303196 | 2,668038 | -0,65804 | 32,73823 | 0,433015 | |
| Архангельская обл. | 0,452 | 0,903573 | 2,945627 | -0,11563 | 4,085775 | 0,01337 | |
| Вологодская обл. | 0,539 | 1,617228 | 3,252097 | 0,207903 | 6,008746 | 0,043223 | |
| Новгородская обл. | 0,601 | 2,403892 | 3,590453 | 0,399547 | 10,0137 | 0,159638 | |
| Ростовская обл. | 0,65 | 3,251538 | 3,964012 | 0,505988 | 11,31963 | 0,256023 | |
| Орловская обл. | 0,689 | 4,135853 | 4,376438 | 0,513562 | 10,5023 | 0,263746 | |
| Ярославская обл. | 0,723 | 5,06419 | 4,831772 | 0,458228 | 8,662149 | 0,209973 | |
| Калужская обл. | 0,752 | 6,016388 | 5,334481 | 0,315519 | 5,584403 | 0,099552 | |
| Ленинградская обл. | 0,779 | 7,00987 | 5,889493 | 0,120507 | 2,005106 | 0,014522 | |
| Мурманская обл. | 0,801 | 8,007171 | 6,50225 | -0,18225 | 2,883699 | 0,033215 | |
| Респ. Коми | 0,822 | 9,036649 | 7,178759 | -0,54876 | 8,276909 | 0,301137 | |
| Московская. обл. | 0,84 | 10,08127 | 7,925654 | -1,00565 | 14,53257 | 1,01134 | |
| ИТОГО | 7,951 | 57,83082 | 116,6132 | 2,838753 | |||
| Среднее | 6,5 | 0,663 | 4,819235 | 9,717769 | 0,236563 | ||
| Дисперсия | 11,9167 | 0,025 |
Рассчитаем 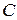 и
и  :
:
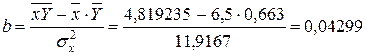 ,
,
 .
.
Получим линейное уравнение  .
.
Выполнив его потенцирование, получим:
 .
.
Подставляя в уравнение регрессии фактические значения  , определим теоретические (расчетные) значения
, определим теоретические (расчетные) значения  . По ним рассчитаем показатели: тесноты связи- индекс корреляции
. По ним рассчитаем показатели: тесноты связи- индекс корреляции  и среднюю ошибку аппроксимации:
и среднюю ошибку аппроксимации:
 . Связь сильная. Коэффициент детерминации
. Связь сильная. Коэффициент детерминации 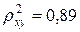 , значит, вариация результата на 89 % объясняется вариацией фактора
, значит, вариация результата на 89 % объясняется вариацией фактора  , а на 11 % вариацией неучтенных в модели признаков.
, а на 11 % вариацией неучтенных в модели признаков.
Величина средней ошибки аппроксимации 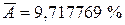 говорит о не очень хорошем, но все же удовлетворительном качестве модели, поскольку
говорит о не очень хорошем, но все же удовлетворительном качестве модели, поскольку  близко к 10%.
близко к 10%.
Оценим теперь статистическую надежность полученной модели с помощью F-критерия Фишера. Выдвигаем гипотезу  о статистической незначимости уравнения регрессии и показателя тесноты связи.
о статистической незначимости уравнения регрессии и показателя тесноты связи.
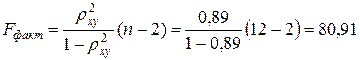 .
.
 .
.
Так как  , то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.
, то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.
Г) Уравнение равносторонней гиперболы 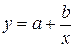 линеаризуется при замене
линеаризуется при замене  . Тогда
. Тогда 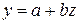 .
.
Для расчетов используем данные таблицы 2.2.5.
Таблица 2.2.5
| Район | 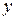
| 
| 
| 
| 
| 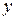 - - 
| 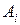
| 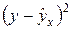
|
| Респ. Карелия | 2,01 | 2,01 | 1,085765 | 0,924235 | 45,98182 | 0,85421 | ||
| Арханг. обл. | 2,83 | 0,5 | 0,25 | 1,415 | 3,639541 | -0,80954 | 28,60571 | 0,655357 |
| Вологод. обл. | 3,46 | 0,33 | 0,111111 | 1,153333 | 4,4908 | -1,0308 | 29,79191 | 1,062549 |
| Новгород. обл. | 3,99 | 0,25 | 0,0625 | 0,9975 | 4,916429 | -0,92643 | 23,21878 | 0,858272 |
| Рост. обл. | 4,47 | 0,2 | 0,04 | 0,894 | 5,171807 | -0,70181 | 15,70038 | 0,492533 |
| Орлов. обл. | 4,89 | 0,17 | 0,027778 | 0,815 | 5,342059 | -0,45206 | 9,244557 | 0,204357 |
| Ярослав.обл. | 5,29 | 0,14 | 0,020408 | 0,755714 | 5,463667 | -0,17367 | 3,282934 | 0,03016 |
| Калужск. обл. | 5,65 | 0,13 | 0,015625 | 0,70625 | 5,554874 | 0,095126 | 1,683655 | 0,009049 |
| Ленингр..обл. | 6,01 | 0,11 | 0,012346 | 0,667778 | 5,625812 | 0,384188 | 6,392484 | 0,147601 |
| Мурман. обл. | 6,32 | 0,1 | 0,01 | 0,632 | 5,682562 | 0,637438 | 10,08604 | 0,406327 |
| Респ. Коми | 6,63 | 0,090909 | 0,008264 | 0,602727 | 5,728995 | 0,901005 | 13,58983 | 0,811811 |
| Москов.обл. | 6,92 | 0,083333 | 0,006944 | 0,576667 | 5,767688 | 1,152312 | 16,6519 | 1,327823 |
| Среднее | 4,8725 | 0,258601 | 0,130415 | 0,935497 | 17,01917 | 0,571671 | ||
| Дисперсия | 2,229252 | 0,06354 |
Рассчитаем параметры  и
и  .
.
 ,
,
 .
.
Получено уравнение  .
.
Подставляя в уравнение регрессии фактические значения  , определим теоретические (расчетные) значения
, определим теоретические (расчетные) значения  . По ним рассчитаем показатели: тесноты связи - индекс корреляции
. По ним рассчитаем показатели: тесноты связи - индекс корреляции  и среднюю ошибку аппроксимации:
и среднюю ошибку аппроксимации:
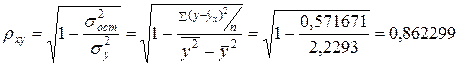 . Связь сильная. Коэффициент детерминации
. Связь сильная. Коэффициент детерминации  , значит, вариация результата на 74 % объясняется вариацией фактора
, значит, вариация результата на 74 % объясняется вариацией фактора  , а на 26 % вариацией неучтенных в модели признаков.
, а на 26 % вариацией неучтенных в модели признаков.
Величина средней ошибки аппроксимации  говорит неудовлетворительном качестве модели, поскольку
говорит неудовлетворительном качестве модели, поскольку  превышает 10%.
превышает 10%.
Оценим теперь статистическую надежность полученной модели с помощью F-критерия Фишера. Выдвигаем гипотезу  о статистической незначимости уравнения регрессии и показателя тесноты связи.
о статистической незначимости уравнения регрессии и показателя тесноты связи.
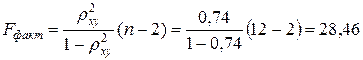 .
.
 .
.
Так как  , то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.
, то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.
Проведённые исследования показывают, что рассматриваемую в задаче зависимость лучше всего описывает степенная кривая, поскольку для этой модели показатель корреляции оказался больше, а ошибка аппроксимации меньше, чем для других построенных функций, при этом уравнение степенной регрессии статистически надёжно.
Пример 2.2.2
По 14 территориям Уральского и Западно-Сибирского района по данным за ноябрь 1997 г. изучалась зависимость потребительских расходов на душу населения (тыс.руб.,  ) от средней заработной платы и выплат социального характера (тыс.руб.,
) от средней заработной платы и выплат социального характера (тыс.руб.,  ). Было получено следующее уравнение линейной регрессии
). Было получено следующее уравнение линейной регрессии  ,
, 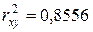 . Известны следующие данные
. Известны следующие данные 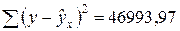 ,
, 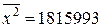 ,
, 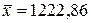 .
.
Задание.
1. Оценить статистическую значимость параметров регрессии и корреляции.
2. Выполнить прогноз потребительских расходов на душу населения, если значение средней заработной платы и выплат социального характера увеличится на 6% от своего среднего уровня.
3. Определить доверительны
|
|
|


