 |
Система линейных эконометрических уравнений
|
|
|
|
Краткая теория
Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений.
Различают несколько видов систем уравнений:
· система независимых уравнений – когда каждая зависимая переменная 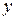 рассматривается как функция одного и того же набора факторов
рассматривается как функция одного и того же набора факторов  :
:
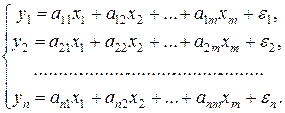
· система рекурсивных уравнений - когда зависимая переменная 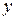 одного уравнения выступает в виде фактора в другом уравнении:
одного уравнения выступает в виде фактора в другом уравнении:
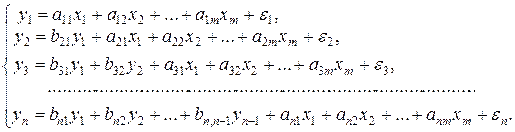
· система взаимосвязанных (совместных) уравнений – когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а другие в правую:

Такая система уравнений называется структурной формой модели.
Эндогенные переменные – взаимозависимые переменные, которые определяются внутри системы (модели) 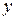 .
.
Экзогенные переменные – независимые переменные, которые определяются вне системы  .
.
Лаговые эндогенные переменные – эндогенные переменные за предыдущие моменты времени.
Предопределенные переменные – экзогенные и лаговые эндогенные переменные системы.
Коэффициенты  и
и  при переменных – структурные коэффициенты модели.
при переменных – структурные коэффициенты модели.
Система линейных функций эндогенных переменных от всех предопределенных переменных системы – приведенная форма модели:
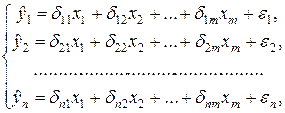
где 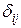 - коэффициенты приведенной формы модели.
- коэффициенты приведенной формы модели.
Необходимое условие идентификации – выполнение счетного правила:
 -уравнение идентифицируемо;
-уравнение идентифицируемо;
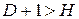 -уравнение сверхидентифицируемо;
-уравнение сверхидентифицируемо;
 -уравнение неидентифицируемо,
-уравнение неидентифицируемо,
где  - число эндогенных переменных в уравнении,
- число эндогенных переменных в уравнении, 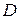 - число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
- число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
Достаточное условие идентификации – определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
|
|
|
Для решения идентифицируемого уравнения применяется косвенный метод наименьших квадратов, для решения сверхидентифицированных - двухшаговый метод наименьших квадратов.
Косвенный МНК состоит в следующем:
· составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
· путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
Двухшаговый МНК заключается в следующем:
· составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
· выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяются двухшаговым МНК, и находят расчетные значения этих эндогенных переменных по соответствующим уравнениям приведенной системы;
· обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части уравнения.
Примеры решения задач
Пример 4.2.1
Рассматривается модель протекционизма Сальватора (упрощенная версия):

где 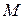 - доля импорта в ВВП;
- доля импорта в ВВП;
 -общее число прошений об освобождении от таможенных пошлин;
-общее число прошений об освобождении от таможенных пошлин;
 - число удовлетворенных прошений об освобождении от таможенных пошлин;
- число удовлетворенных прошений об освобождении от таможенных пошлин;
 - фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен, и 0-для всех остальных лет;
- фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен, и 0-для всех остальных лет;
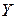 - реальный ВВП;
- реальный ВВП;
 -реальный объем чистого экспорта;
-реальный объем чистого экспорта;
 - текущий период;
- текущий период;
 -предыдущий период.
-предыдущий период.
Задание.
1. Применив необходимое и достаточное условие идентификации определите, идентифицировано ли каждое из уравнений модели.
|
|
|
2. Определите метод оценки параметров модели.
3. Запишите приведенную форму модели в общем виде.
Решение.
1. Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные (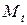 ,
,  ,
,  ) и четыре предопределенные переменные (три экзогенные
) и четыре предопределенные переменные (три экзогенные  ,
,  ,
, 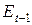 и одну лаговую эндогенную
и одну лаговую эндогенную  ).
).
Проверим необходимое условие идентификации для уравнений модели.
1 уравнение.
Это уравнение включает три эндогенные переменные (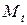 ,
,  ,
,  ) и две предопределенные (
) и две предопределенные (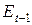 и
и  ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, равно числу эндогенных переменных, входящих в уравнение: 2+1=3. Уравнение идентифицировано.
). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, равно числу эндогенных переменных, входящих в уравнение: 2+1=3. Уравнение идентифицировано.
2 уравнение.
Это уравнение включает три эндогенные переменные (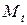 ,
,  ,
,  ) и одну предопределенную (
) и одну предопределенную ( ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 3+1>3. Уравнение сверхидентифицировано.
). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 3+1>3. Уравнение сверхидентифицировано.
3 уравнение.
Это уравнение включает три эндогенные переменные (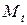 ,
,  ,
,  ) и одну предопределенную (
) и одну предопределенную ( ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 3+1>3. Уравнение сверхидентифицировано.
). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 3+1>3. Уравнение сверхидентифицировано.
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели:
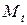
| 
| 
| 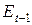
| 
| 
| 
| |
| 1 уравнение | -1 | 
| 
| 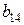
| 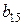
| ||
| 2 уравнение | 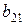
| -1 | 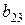
| 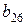
| |||
| 3 уравнение | 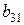
| 
| -1 | 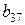
|
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее, чем число эндогенных переменных модели минус 1, т.е. в данной задаче больше или равен 3-1=2.
1 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
 .
.
Ее определитель 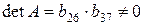 . Ранг этой матрицы
. Ранг этой матрицы 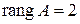 . Следовательно, для 1 уравнения достаточное условие выполняется, это уравнение точно идентифицируемо.
. Следовательно, для 1 уравнения достаточное условие выполняется, это уравнение точно идентифицируемо.
|
|
|
2 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
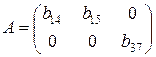 .
.
Ранг этой матрицы 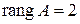 , так как она содержит отличный от нуля минор второго порядка
, так как она содержит отличный от нуля минор второго порядка  . Следовательно, для 2 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо.
. Следовательно, для 2 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо.
3 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
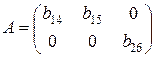 .
.
Ранг этой матрицы 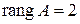 , так как она содержит отличный от нуля минор второго порядка
, так как она содержит отличный от нуля минор второго порядка 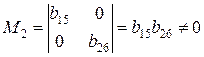 . Следовательно, для 3 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо.
. Следовательно, для 3 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо.
2. Таким образом, система в целом сверхидентифицируема, для оценки ее параметров можно применить двухшаговый метод наименьших квадратов.
3. Запишем приведенную форму модели в общем виде:
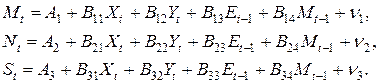
Пример 4.2.2
Рассматривается структурная модель вида:
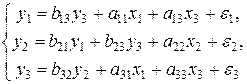
Задание.
1. Применив необходимое и достаточное условие идентификации определите, идентифицировано ли каждое из уравнений модели.
2. Определите метод оценки параметров модели.
3. Запишите приведенную форму модели в общем виде.
Решение.
1. Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные (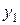 ,
, 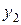 ,
, 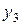 ) и три предопределенные переменные (экзогенные
) и три предопределенные переменные (экзогенные  ,
,  ,
,  ).
).
Проверим необходимое условие идентификации для уравнений модели.
1 уравнение.
Это уравнение включает две эндогенные переменные (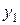 и
и 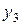 ) и две предопределенные (
) и две предопределенные ( и
и  ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, равно числу эндогенных переменных, входящих в уравнение: 1+1=2. Уравнение идентифицировано.
). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, равно числу эндогенных переменных, входящих в уравнение: 1+1=2. Уравнение идентифицировано.
2 уравнение.
Это уравнение включает три эндогенные переменные (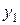 ,
, 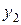 ,
, 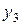 ) и одну предопределенную (
) и одну предопределенную ( ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, равно числу эндогенных переменных, входящих в уравнение: 2+1=3. Уравнение идентифицировано.
). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, равно числу эндогенных переменных, входящих в уравнение: 2+1=3. Уравнение идентифицировано.
3 уравнение.
Это уравнение включает две эндогенные переменные (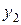 и
и 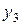 ) и две предопределенные (
) и две предопределенные ( и
и  ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, равно числу эндогенных переменных, входящих в уравнение: 1+1=2. Уравнение идентифицировано.
). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, равно числу эндогенных переменных, входящих в уравнение: 1+1=2. Уравнение идентифицировано.
|
|
|
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели:
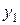
| 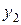
| 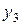
| 
| 
| 
| |
| 1 уравнение | -1 | 
| 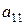
| 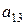
| ||
| 2 уравнение | 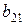
| -1 | 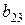
| 
| ||
| 3 уравнение | 
| 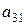
| 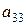
|
1 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
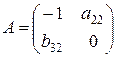 .
.
Определитель матрицы  , а ранг матрицы
, а ранг матрицы 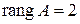 , что не менее чем число эндогенных переменных системы минус один. Следовательно, для первого уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
, что не менее чем число эндогенных переменных системы минус один. Следовательно, для первого уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
2 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
 .
.
Определитель матрицы  , а ранг матрицы
, а ранг матрицы 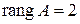 , что не менее чем число эндогенных переменных системы минус один. Следовательно, для второго уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
, что не менее чем число эндогенных переменных системы минус один. Следовательно, для второго уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
3 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
 .
.
Определитель матрицы 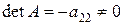 , а ранг матрицы
, а ранг матрицы 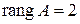 , что не менее чем число эндогенных переменных системы минус один. Следовательно, для третьего уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
, что не менее чем число эндогенных переменных системы минус один. Следовательно, для третьего уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
2. Все уравнения системы точно идентифицируемы, следовательно, система в целом точно идентифицируема, для оценки ее параметров может быть применен косвенный метод наименьших квадратов.
3. Запишем приведенную форму модели в общем виде:

|
|
|


