Проводник во внешнем электрическом поле.

Если проводнику сообщить избыточный заряд, то этот заряд распределится по поверхности проводника. Действительно, если внутри проводника выделить произвольную замкнутую поверхность S, то поток вектора напряженности электрического поля через эту поверхность должен быть равен нулю. В противном случае внутри проводника будет существовать электрическое поле, что приведет к перемещению зарядов. Следовательно, для того, чтобы выполнялось условие

,

суммарный электрический заряд внутри этой произвольной поверхности должен равняться нулю.

Напряженность электрического поля вблизи поверхности заряженного проводника можно определить, используя теорему Гаусса. Для этого выделим на поверхности проводника малую произвольную площадку d S и, считая ее за основание, построим на ней цилиндр с образующей d l (рис. 3.1). На поверхности проводника вектор Е направлен по нормали к этой поверхности. Поэтому поток вектора Е через боковую поверхность цилиндра из-за малости d l равен нулю. Поток этого вектора через нижнее основание цилиндра, находящееся внутри проводника, также равен нулю, так как внутри проводника электрическое поле отсутствует. Следовательно, поток вектора Е через всю поверхность цилиндра равен потоку через его верхнее основание d S^':

 

,

где Е_n - проекция вектора напряженности электрического поля на внешнюю нормаль n к площадке d S.

По теореме Гаусса, этот поток равен алгебраической сумме электрических зарядов, охватываемых поверхностью цилиндра, отнесенной к произведению электрической постоянной и относительной диэлектрической проницаемости среды, окружающей проводник. Внутри цилиндра находится заряд , где 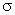- поверхностная плотность зарядов. Следовательно 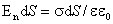и , т. е. напряженность электрического поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности электрических зарядов, находящихся на этой поверхности.

Экспериментальные исследования распределения избыточных зарядов на проводниках различной формы показали, что распределение зарядов на внешней поверхности проводника зависит только от формы поверхности: чем больше кривизна поверхности (чем меньше радиус кривизны), тем больше поверхностная плотность заряда.

Вблизи участков с малыми радиусами кривизны, особенно около острия, из-за высоких значений напряженности происходит ионизация газа, например, воздуха. В результате одноименные с зарядом проводника ионы движутся в направлении от поверхности проводника, а ионы противоположного знака к поверхности проводника, что приводит к уменьшению заряда проводника. Это явление получило название стекания заряда.

На внутренних поверхностях замкнутых полых проводников избыточные заряды отсутствуют.

Если заряженный проводник привести в соприкосновение с внешней поверхностью незаряженного проводника, то заряд будет перераспределяться между проводниками до тех пор, пока их потенциалы не станут равными.

Если же тот же заряженный проводник касается внутренней поверхности полого проводника, то заряд передается полому проводнику полностью.
Эта особенность полых проводников была использована американским физиком Робертом Ван-де-Граафом для создания в 1931 г. электростатического генератора, в котором высокое постоянное напряжение создается посредством механического переноса электрических зарядов. Наиболее совершенные электростатические генераторы позволяют получать напряжение величиной до 15 - 20 МВ.

В заключение отметим еще одно явление, присущее только проводникам. Если незаряженный проводник поместить во внешнее электрическое поле, то его противоположные части в направлении поля будут иметь заряды противоположных знаков. Если, не снимая внешнего поля, проводник разделить, то разделенные части будут иметь разноименные заряды. Это явление получило название электростатической индукции.

 

ЭЛЕКТРОЕМКОСТЬ.

Рассмотрим уединенный проводник, т. е. проводник, находящийся в однородной изотропной среде вдали от других проводников и заряженных тел. При сообщении такому проводнику избыточного заряда q последний распределяется по поверхности проводника с поверхностной плотностью 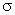, которая зависит от размеров и формы проводника.
Выделим на поверхности проводника малый элемент площади d S, полагая, что заряд этого элемента является точечным. В другой точке поверхности этого же проводника, отстоящей от элемента d S на расстояние r, этот заряд создает электрическое поле, потенциал которого равен

,где - относительная диэлектрическая проницаемость среды, в которой находится проводник. Интегрируя это выражение по всей поверхности проводника S, найдем потенциал, создаваемый в рассматриваемой точке всем проводником:

 

Так как в различных точках на поверхности проводника поверхностная плотность заряда имеет разные значения, то будем полагать, что 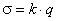, где k - некоторая функция координат выбранного элемента поверхности d S. Тогда выражение для потенциала проводника имеет вид

 

. (3.1)

В полученном выражении интеграл зависит от размеров и формы поверхности проводника, а также от расположения точки, для которой определяется потенциал.

Значения этого интеграла не зависят от величины заряда, сообщенного проводнику, т. е. одинаковы при различных значениях заряда q.

Из формулы (3.1) следует, что потенциал уединенного проводника прямо пропорционален его заряду и отношение заряда q к потенциалу для данного проводника есть величина постоянная. Это отношение называется электрической емкостью, или электроемкостью, проводника:

 

Электрическая емкость уединенного проводника зависит от его формы и размеров, а также от величины относительной диэлектрической проницаемости среды, в которой он находится. Электроемкость не зависит от материала проводника, его агрегатного состояния, от формы и размеров возможных полостей внутри проводника. Электроемкость не зависит также ни от заряда проводника, ни от его потенциала.

В качестве примера найдем электроемкость уединенного проводящего шара радиуса R, покрытого слоем диэлектрика с относительной проницаемостью и толщиной d. Пусть шар имеет заряд q. Тогда напряженность поля, создаваемого шаром внутри диэлектрического слоя,

 

За пределами слоя напряженность поля определяется выражением:

 

Потенциал поверхности шара:

 

Таким образом, электроемкость шара, покрытого слоем диэлектрика, есть

 

В случае, если толщина диэлектрического слоя , емкость шара равна 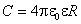. При d =0 она равна .

Из приведенных соотношений следует, что потенциалы одинаково заряженных и геометрически подобных проводников должны быть обратно пропорциональны их линейным размерам, а их электрические емкости прямо пропорциональны этим размерам.

Электроемкость проводника численно равна заряду, который нужно сообщить этому проводнику для изменения его потенциала на единицу. В СИ единица измерения электрической емкости 1 фарада (Ф). Это емкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл: 1 Ф = 1 Кл / 1 В.
Если вблизи проводника есть другие проводящие незаряженные тела, то при сообщении проводнику некоторого электрического заряда его потенциал будет меньше, чем потенциал уединенного проводника таких же формы и размеров. Это обусловлено тем, что на поверхностях тел, обращенных к заряженному проводнику, будут индуцироваться электрические заряды противоположного знака.
Для наглядности поясним это явление на примере. Пусть на некотором расстоянии от проводящего шара радиуса R расположен незаряженный металлический стержень длиной l так, что его ближний конец находится на расстоянии r от центра шара, а дальний - на расстоянии (r + l). Если шару сообщить положительный электрический заряд Q, то создаваемое шаром поле будет индуцировать на ближнем конце стержня заряд -q, а на дальнем заряд + q. Потенциал шара при этом будет равен

 

Следовательно, электроемкость проводника возрастает, если недалеко от него находятся другие проводящие тела. В этом случае принято говорить о взаимной электроемкости проводников.

Наибольший интерес представляет взаимная электроемкость системы из двух проводников с равными по величине и противоположными по знаку электрическими зарядами: |+ q | = |- q | = q. Их взаимная электрическая емкость определяется как отношение заряда к разности потенциалов ,где разность потенциалов между проводниками.

 

КОНДЕНСАТОРЫ.

Если два проводника имеют такую форму, что создаваемое ими электрическое поле сосредоточено в ограниченной области пространства, то образованная ими система носит название конденсатора, а сами проводники называют обкладками конденсатора.

Сферический конденсатор. Два проводника, имеющие форму концентрических сфер с радиусами R ₁ и R ₂ (R ₂ > R ₁), образуют сферический конденсатор. Используя теорему Гаусса, легко показать, что электрическое поле существует только в пространстве между сферами. Напряженность этого поля

,

где q - электрический заряд внутренней сферы; - относительная диэлектрическая проницаемость среды, заполняющей пространство между обкладками; r - расстояние от центра сфер, причем R ₁ r R ₂. Разность потенциалов между обкладками

 

и емкость сферического конденсатора

 

.

Цилиндрический конденсатор представляет собой два проводящих коаксиальных цилиндра радиусами R ₁ и R ₂ (R ₂ > R ₁). Пренебрегая краевыми эффектами на торцах цилиндров и считая, что пространство между обкладками заполнено диэлектрической средой с относительной проницаемостью , напряженность поля внутри конденсатора можно найти по формуле:

 

,

где q - заряд внутреннего цилиндра; h - высота цилиндров (обкладок); r - расстояние от оси цилиндров. Соответственно, разность потенциалов между обкладками цилиндрического конденсатора и его емкость есть

 

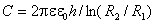
Плоский конденсатор. Две плоские параллельные пластины одинаковой площади S, расположенные на расстоянии d друг от друга, образуют плоский конденсатор. Если пространство между пластинами заполнено средой с относительной диэлектрической проницаемостью , то при сообщении им заряда q напряженность электрического поля между пластинами равна , разность потенциалов равна . Таким образом, емкость плоского конденсатора .

Последовательное и параллельное соединение конденсаторов. При последовательномсоединении n конденсаторов суммарная емкость системы равна

 

Параллельное соединение n конденсаторов образует систему, электроемкость которой можно вычислить следующим образом:

 

ЭЛЕКТРИЧЕСКИЙ ТОК.

Если через некоторую поверхность переносится суммарный заряд, отличный от нуля, то говорят, что через эту поверхность течет электрический ток. Ток может протекать в твердых телах, в жидкостях и в газах. Для протекания тока необходимо наличие в данном теле (или в данной среде) заряженных частиц, которые могут перемещаться в пределах всего тела. Такие частицы называются носителями тока. Ими могут быть электроны, ионы либо макроскопические частицы (например, заряженные пылинки, капельки), несущие избыточный заряд.

Направлением тока условились считать направление движения положительно заряженных частиц. Линии, вдоль которых движутся заряженные частицы, названы линиями тока. Для количественной характеристики электрического тока служат две основные величины: плотность тока и сила тока.

Плотность тока равна заряду, проходящему в единицу времени через единицу поверхности, которая перпендикулярна к линиям тока. Пусть в единице объема содержится положительных носителей тока и отрицательных.

Алгебраическая величина зарядов носителей тока равна, соответственно, и . Если под действием поля носители тока приобретают средние скорости движения и , то за единицу времени через единичную площадку пройдет положительных носителей тока, которые перенесут заряд . Аналогично отрицательные носители перенесут в противоположную сторону заряд . Таким образом, для плотности тока получается следующее выражение:

.

Или в векторном виде вектор плотности тока j определяется следующим образом

 

.

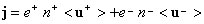Если в поперечном сечении проводника выделить бесконечно малую площадку d S, перпендикулярную вектору плотности тока j, то заряд d q, проходящий через нее за время d t, равен

 

.

Сила тока в проводнике равна заряду, проходящему в единицу времени через полное сечение проводника. Если заряд d q, проходящий через сечение проводника за время d t, то

 

.

Сила тока скалярная величина. Зная вектор плотности тока в каждой точке проводника, можно выразить через него и силу тока

 

.

Размерность силы тока - ампер (А), единица измерения плотности тока - ампер на метр квадратный (). Если сила тока не меняется во времени, то ток, протекающий в проводнике, называют постоянным. Силу постоянного тока будем обозначать буквой I.

Рассмотрим среду, в которой течет ток, и выделим в ней замкнутую поверхность S (рис. 4.1). Для тока, выходящего в единицу времени из объема V, ограниченного поверхностью S, имеем

 

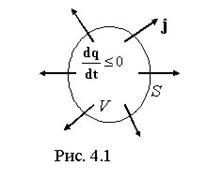
В силу закона сохранения заряда эта величина должна быть равна скорости убывания заряда, содержащегося в данном объеме

 

.
Это соотношение называют уравнением непрерывности. Учитывая, что заряд

,

получим 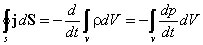. Преобразовав левую часть равенства по теореме о дивергенции (теореме Гаусса - Остроградского), находим

 

.

Таким образом в каждой точке пространства выполняется условие

 

,

которое является дифференциальной формой уравнения непрерывности.

Если токи постоянны, то все электрические величины не зависят от времени и в уравнении непрерывности нужно положить равным нулю. Тогда , следовательно, в случае постоянного тока вектор j не имеет источников. Это означает, что линии тока нигде не начинаются и нигде не заканчиваются, т. е. они замкнуты.

 

 

ЭЛЕКТРОДВИЖУЩАЯ СИЛА.

Смещение под действием электрического поля зарядов в проводнике всегда происходит таким образом, что электрическое поле в проводнике исчезает и ток прекращается. Для протекания тока в течение продолжительного времени на заряды в электрической цепи должны действовать силы, отличные по природе от сил электростатического поля, такие силы получили название сторонних сил.
Эти силы могут быть обусловлены химическими процессами, диффузией носителей тока в неоднородной среде, электрическими (но не электростатическими) полями, порождаемыми переменными во времени магнитными полями, и т. д. Всякое устройство, в котором возникают сторонние силы, называется источником электрического тока.
Сторонние силы характеризуют работой, которую они совершают над перемещаемыми по электрической цепи носителями заряда.

Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС) , действующей в электрической цепи или на ее участке.

Представим стороннюю силу , действующую на заряд q, в виде

,

где векторная величина представляет напряженность поля сторонних сил. Тогда на участке цепи ЭДС равна

 

Интеграл, вычисленный для замкнутой цепи, дает ЭДС, действующую в этой цепи,

 

.

Последнее выражение дает самое общее определение ЭДС и пригодно для любых случаев. Если известно, какие силы вызывают движение зарядов в данном источнике, то всегда можно найти напряженность поля сторонних сил и вычислить ЭДС источника. Физическая природа электродвижущих сил в разных источниках весьма различна.

 

Рассмотрим пример. Пусть имеется металлический диск радиуса R (рис. 4.2), вращающийся с угловой скоростью . Диск включен в электрическую цепь при помощи скользящих контактов, касающихся оси диска и его окружности. Центростремительная сила 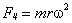, где m - масса электрона; r - расстояние от оси диска. Эта сила действует на электрон и поэтому , возникающая ЭДС равна

 

.

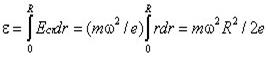ЗАКОН ОМА.

Немецкий физик Г. Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному (отсутствуют сторонние силы) металлическому проводнику, пропорциональна падению напряжения на проводнике:

.

Сопротивление проводника. Величина R называется электрическим сопротивлением проводника. Единица сопротивления - 1 Ом. Для однородного цилиндрического проводника

 

где l - длина проводника; S - площадь его поперечного сечения; - зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением. В системе СИ единица измерения есть .
Дифференциальная форма закона Ома. Найдем связь между плотностью тока j и напряженностью поля Е в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора Е. Поэтому направления векторов j и Е совпадают.
Рассмотрим в однородной изотропной среде элементарный объем с образующими, параллельными вектору Е, длиной , ограниченной двумя эквипотенциальными сечениями 1 и 2 (рис. 4.3).

 

Обозначим их потенциалы и , а среднюю площадь сечения через . Используя закон Ома, получим для тока , или для плотности тока , следовательно

 

.

Перейдем к пределу при , тогда рассматриваемый объем можно считать цилиндрическим, а поле внутри него однородным, так что

 

,

где Е - напряженность электрического поля внутри проводника. Учитывая, что j и Е совпадают по направлению, получаем

 

.

Это соотношение является дифференциальной формой закона Ома для однородного участка цепи. Величина называется удельной проводимостью.

На неоднородном участке цепи на носители тока действуют, кроме электростатических сил , еще и сторонние силы , следовательно, плотность тока в этих участках оказывается пропорциональной сумме напряженностей. Учет этого приводит к дифференциальной форме закон Ома для неоднородного участка цепи.

 

.

От закона Ома в дифференциальной форме легко перейти к интегральной форме. Рассмотрим неоднородный участок цепи. Внутри этого участка выберем контур тока, удовлетворяющий следующим условиям: в каждом сечении, перпендикулярном к контуру, величины имеют с достаточной точностью одинаковые значения; векторы в каждой точке направлены по касательной к контуру.

Вследствие закона сохранения заряда сила постоянного тока в каждом сечении должна быть одинаковой. Поэтому величина постоянна вдоль контура. Тогда, заменяя j отношением , получаем

 

.

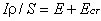Умножим это соотношение на d l и проинтегрируем вдоль контура:

 

,

где представляет собой суммарное сопротивление участка цепи, первый интеграл в правой части - разность потенциалов на концах участка, а второй интеграл определяет ЭДС 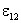, действующую на участке цепи. Таким образом .

ЭДС 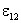, как и сила тока I, величина алгебраическая. В случае, когда ЭДС способствует движению положительных носителей тока в выбранном направлении (в направлении 1-2), . Если ЭДС препятствует движению положительных носителей в данном направлении, то :

 

.

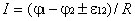Последняя формула выражает закон Ома для неоднородного участка цепи. Для замкнутой цепи закон Ома имеет вид

 

,

где R - сопротивление нагрузки, r - внутреннее сопротивление источника тока.

 

ЗАКОН ДЖОУЛЯ-ЛЕНЦА.

Рассмотрим произвольный участок цепи постоянного тока, к концам которого приложено напряжение U. За время t через каждое сечение проводника проходит заряд 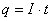. Это равносильно тому, что заряд q переносится за время t из одного конца проводника в другой.

При этом силы электростатического поля и сторонние силы, действующие на данном участке, совершают работу . Разделив работу на время t, за которое она совершается, получим мощность, развиваемую током на рассматриваемом участке .

Эта мощность может расходоваться на совершение работы над внешними телами; на протекание химических реакций; на нагревание данного участка цепи и др.

В случае, когда проводник неподвижен и химических превращений в нем не совершается, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается. Принято говорить, что при протекании тока в проводнике выделяется тепло

(4.1)

Это соотношение называется законом Джоуля - Ленца. Оно было экспериментально установлено английским физиком Д. П. Джоулем и подтверждено точными опытами Э. Х. Ленца.

Если сила тока изменяется со временем, то количество теплоты, выделяющееся в проводнике за время t, вычисляется по формуле

От формулы (4.1), можно перейти к выражению, характеризующему выделение тепла в различных точках проводника. Выделим в проводнике элементарный объем в виде цилиндра. Согласно закону Джоуля - Ленца, за время d t, в этом объеме выделится количество теплоты

 

,

где - d V элементарный объем. Разделив это выражение на d V и d t, найдем количество теплоты, выделяющееся в единице объема в единицу времени:

 

.

Величину называют удельной тепловой мощностью тока. Эта формула представляет собой дифференциальную форму закона Джоуля - Ленца.

 

 

22. ПОРАЖЕНИЕ ЭЛЕКТРИЧЕСКИМ ТОКОМ ЧЕЛОВЕКА В РАЗНЫХ СИТУАЦИЯХ.
Поражение электричеством может иметь место в следующих формах: остановка сердца или дыхания при прохождении электрического тока через тело; ожог; механическая травма из-за сокращения мышц под действием тока; ослепление электрической дугой. Смерть обычно наступает из-за остановки сердца или дыхания, или того и другого.

Переменный ток и постоянный ток опасны почти в одинаковой степени. 90 % травм происходит из-за плохой организации фуда и только 10 % - по вине пострадавших.
Действие электрического тока на живую ткань носит разносторонний и своеобразный характер. Проходя через тело человека, электроток производит термическое, электролитическое, механическое и биологическое действие.
Ток, проходящий через тело человека, зависит от напряжения прикосновения, под которым оказался пострадавший, и суммарного электрического сопротивления, в которое входит сопротивление тела человека. Величина последнего определяется в основном сопротивлением рогового слоя кожи и составляет при сухой коже и отсутствии повреждений сотни тысяч Ом. Если эти условия состояния кожи не выполняются, то ее сопротивление падает до 1 кОм. При высоком напряжении и значительном времени протекания тока через тело сопротивление кожи падает еще быстрее и способствует более тяжелым последствиям поражения током. Внутреннее сопротивление тела человека не превышает нескольких сот Ом и существенной роли не играет.

На сопротивление организма воздействию электрического тока оказывает влияние физическое и психическое состояние человека.

Нездоровье, утомление, голод, опьянение, эмоциональное возбуждение приводят к снижению сопротивления.

Характер воздействия тока на человека зависит от силы и рода тока. Для переменного тока частотой 50 Гц, напряжением 220 В и пути тока — «рука — нога» сила тока 0,6 - 1,5 мА является ощутимой, появляется легкое дрожание пальцев. При силе тока 2,0 - 2,5 мА возникают болевые ощущения, а при 5,0 - 7,0 мА —судороги в руках; 20,0 - 25,0 мА —это неотпускающий ток, человек не может самостоятельно оторвать руки от электродов, наблюдаются сильные боли и судороги, затрудненное дыхание, а при 50,0 - 80,0 мА—паралич дыхания; 90,0 - 100,0 мА— наступает фибрилляция сердца при действии тока в течение 2-3 с и паралич дыхания.

Допустимым следует считать ток, при котором человек может самостоятельно освободиться от электрической цепи. Его величина зависит от скорости прохождения тока через тело человека: при длительности действия более 10 с —2 мА, а при —120 с и менее — 6 мА. Переменный ток более опасен, чем постоянный, однако при высоком напряжении (более 500 В) опаснее становится постоянный ток. Из всех возможных путей протекания тока через тело человека (голова —рука, голова —нога, рука —рука, нога —рука, нога —нога и т. д.) наиболее опасен тот, при котором поражаются головной мозг, сердце и легкие.

Электрическое сопротивление человеческого тела имеет иную природу, чем сопротивление металлических проводников и электролитов.

Оно зависит от многих внешних и внутренних (в том числе психических) факторов. Больше всего от действия электрического тока страдает центральная нервная система. Из-за повреждения ее нарушаются дыхание и сердечная деятельность. Участки тела с наименьшим сопротивлением (т.е. более уязвимые): боковые поверхности шеи; виски, тыльная сторона ладони; поверхность ладони между большим и указательным пальцами; рука на участке выше кисти; плечо; спина; передняя часть ноги; акупунктурные точки, расположенные в разных местах тела.

Электроожоги излечиваются значительно труднее обычных термических. Некоторые последствия электротравмы могут проявиться через несколько часов, дней, месяцев. Пострадавший должен длительное время жить в "шядящемм режиме и находиться под наблюдемнием.

Поражения электрическим током происходят при контакте части человеческого тела с любым источником электричества, который вызывает прохождение тока достаточной силы через кожу, мышцы или волосы. Как правило, это выражение используется для описания травмирующего воздействия электричества. Токи малой силы могут быть незаметны. Более сильные токи, проходящие через тело, могут вызвать спазм мышц, в результате которого жертва поражения электрическим током не сможет отпустить источник напряжения. Еще большие токи могут вызвать фибрилляцию сердца и повреждение тканей тела. Когда травмы от удара электричества несовместимы с жизнью, наступает смерть от поражения электрическим током.

Сила электрического тока

Минимальная сила тока, который может почувствовать человек, зависит от типа тока (переменный или постоянный) и от его частоты. Человек способен ощутить минимальный переменный ток силой (в среднем) 1 мА с частотой 60 Гц, в то время как для постоянного тока минимальная величина будет равна 5 мА. Переменный ток силой приблизительно 10 мА, проходящий через руку человека, может заставить сократиться ее мышцы с силой 68 килограммов; при этом жертва не в состоянии контролировать свои мышцы и не может освободиться от объекта электрического тока. Это явление известно как «порог отпускания» и является критерием опасности удара при обращении с электрическим током. Электроток достаточно высокой силы может вызвать повреждение тканей или фибрилляцию, которая может привести к остановке сердца. Переменный ток силой более 30 мА (при частоте, в среднем, 60 Гц), или 300-500 мА постоянного тока может стать причиной фибрилляции. Длительный удар электрического тока напряжением 120 В при частоте 60 Гц особенно опасен, являясь причиной фибрилляции сердечных желудочков, поскольку при этом обычно превышен порог отпускания, в то время как человек не получает достаточно начальной энергии для того, чтобы отпустить источник тока. Последствия удара электрическим током также зависят от путей его прохождения через тело человека. Если напряжение тока менее 200 В, то кожа человека, точнее, ее роговой слой, вносит основной вклад в сопротивление тела в случае макрошока – прохождении тока между двумя точками контакта на коже. Однако особенностью кожи является нелинейность. Если напряжение превышает 450-600 В, происходит диэлектрический пробой кожи. Защитные свойства кожи снижаются из-за испарения на ее поверхности, и это происходит скорее, если мышцы сокращены из-за превышения порога отпускания в течение длительного времени. Если электрическая цепь замкнута через электроды, введенные в тело, минуя кожу, то вероятность летального исхода намного выше, особенно если путь электротока проходит через сердце. Это явление известно как микрошок. В этом случае для фибрилляции сердца достаточно тока силой всего лишь 10 мкА. Некоторое беспокойство вызывает обстановка в современных больницах, где пациент бывает подключен к множеству электроприборов.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: