 |
Теорема остроградского-гаусса для магнитного поля.
|
|
|
|
Подобно тому, как было введено понятие потока вектора напряженности электрического поля, введем понятие потока вектора магнитной индукции, или магнитного потока. Элементарный магнитный поток 
через малую элементарную площадку 
, которую можно считать плоской, и в окрестности которой магнитное поле можно считать однородным, равен произведению вектора индукции на площадь выделенного элемента поверхности и косинус угла между вектором индукции и нормалью к поверхности:
.
Поток может быть как положительным, так и отрицательным в зависимости от направления нормали к поверхности.
За единицу магнитного потока в системе единиц СИ принят вебер (Вб). 1 Вб – это магнитный поток через поверхность площадью 
, расположенную в однородном магнитном поле перпендикулярно вектору индукции 
, равному по модулю 
:
.
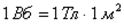В случае неоднородного магнитного поля поток через какую-либо поверхность равен алгебраической сумме потоков через участки поверхности, вблизи которых поле можно считать однородным.
Магнитный поток, как и поток вектора напряженности электрического поля, можно считать равным числу магнитных силовых линий, пересекающих рассматриваемую поверхность. Магнитное поле является вихревым, то есть его линии магнитной индукции замкнуты. Поэтому замкнутая поверхность, помещенная в магнитное поле, пронизывается линиями магнитной индукции так, что любая линия, входящая в эту поверхность, выходит из нее. Следовательно, полный магнитный поток через произвольную замкнутую поверхность равен нулю. Это утверждение носит название теоремы Гаусса для магнитных полей. Равенство нулю магнитного потока через замкнутую поверхность является следствием того, что в природе нет магнитных зарядов, и магнитные поля образуются только электрическими зарядами.
|
|
|
Определим поток напряжённости поля электрических зарядов через некоторую замкнутую поверхность, окружающую эти заряды. Рассмотрим сначала случай сферической поверхности радиуса R, окружающей один заряд, находящийся в ее центре (рис. 13.6). 
Напряженность поля по всей сфере одинакова и равна
Силовые линии направлены по радиусам, т.е. перпендикулярны поверхности сферы 
, следовательно
т.к.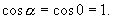 
Тогда поток напряженности 
будет равен
Используя формулу напряжённости, находим
| (13.6) |
Окружим теперь сферу произвольной замкнутой поверхностью S’. Каждая силовая линия, пронизывающая сферу, пронижет и эту поверхность. Следовательно формула (13.6) справедлива не только для сферы, но и для любой замкнутой поверхности. Если произвольной поверхностью окружаем n зарядов, то очевидно, что поток напряженности через эту поверхность равен сумме потоков, создаваемых каждым из зарядов, т.е.
или
| (13.7) |
Таким образом, полный поток вектора напряженности электростатического поля через замкнутую поверхность произвольной формы численно равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности, поделенной на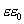 
. Это положение называется теоремой Остроградского - Гаусса. С помощью этой теоремы можно определить напряженность полей, создаваемых заряженными телами различной формы.
МАГНИТНЫЙ ПОТОК.
(поток магнитной индукции), поток Ф вектора магн. индукции В через к.-л. поверхность. М. п. dФ через малую площадку dS, в пределах к-рой вектор В можно считать неизменным, выражается произведением величины площадки и проекции Bn вектора на нормаль к этой площадке, т. е. dФ=BndS. М. п. Ф через конечную поверхность S определяется интегралом: Ф=?SBndS.
Для замкнутой поверхности этот интеграл равен нулю, что отражает соленоидальныйхар-р магнитного поля, т. е. отсутствие в природе магнитных зарядов — источников магн. поля (магн. поля создаются электрич. токами). Единица М. п. в Международной системе единиц (СИ) — вебер, в СГС системе единиц — максвелл; 1 Вб=108 Мкс.
|
|
|
МАГНИТНЫЙ ПОТОК- поток Ф вектора магнитной индукции В через к.-л. поверхность S:
Здесь dS - элемент площади, п - единичный вектор нормали к S. В СИ М. п. измеряется в веберах (Во), в гауссовой системе единиц (к-рая применяется ниже) - в максвеллах (Мкс); 1 Вб=108 Мкс. Поскольку вектор В является чисто вихревым 
, М. п. через произвольную замкнутую поверхность S равен нулю. Это свойство, установленное Гауссом, может нарушаться только при наличии внутри S магнитных монополей, пока ещё гипотетических.
Изменение во времени М. п. ведёт, согласно Максвелла уравнениям (в интегральной форме), к возникновению вихревого электрич. поля Е, циркуляция к-рого по замкнутому контуру l, ограничивающему поверхность S, равна
Здесь направление обхода по l связано с направлением нормали п к S правилом правого винта.
Для проводящих контуров, изготовленных из материалов с достаточно высокой проводимостью (напр., из металлич. провода), соотношение (2) в квазистатич. приближении соответствует закону электромагнитной индукции Фарадея:
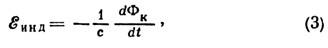
где -эдс эл.-магн. индукции, 
- М. п., "сцепленный" 
с проводящим контуром, т. е. М. п., усреднённый по всем поверхностям Si, опирающимся на линии тока в контуре. В отличие от (2), в (3) берётся полная производная от М. п. по времени в соответствии с тем, что эдс индукции возникает не только при изменении магн. поля во времени, но и при движении проводящего контура поперёк магн. поля, при вращениях и деформациях контура.
М. п., сцепленный со свсрхпроводящим контуром, постоянен во времени и может принимать лишь дискретные (квантованные) значения: 
, где h - постоянная Планка, е - заряд электрона, и - целое число (см. Квантование магнитного потока). Величина кванта М. п. указывает на то, что носители электрич. тока в сверхпроводнике (куперовские пары) имеют заряд 2е.
М. п. может направляться стержнями (обычно ферромагнитными) с магнитной проницаемостью 
(см. Магнитная цепь), подобно тoму как электрич. ток направляется проводами с большой электропроводностью. На границе магнитопровода с окружающим пространством (вакуумом) непрерывна нормальная компонента вектора магн. индукции: 
- внутр. и внеш. поле магн. индукции), а тангенциальная составляющая терпит скачок: 
. Поэтому при 
и при почти произвольной ориентации внеш. магн. поля (исключение составляет случай, когда поле нормально к границе) вектор магн. индукции 
почти параллелен границе и его величина много больше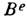 
, а М. п. слабо меняется вдоль магнитопровода. Это свойство ферромагн. материалов широко используется в электротехнике для сосредоточения и переноса М. и. (напр., в трансформаторах, пост.магнитах, якорях электродвигателей).
|
|
|
|
|
|
