З-н Био-СавараЛапласа ( книга физика стр. 207).

Био, Савар и Лаплас установили закон, который позволяет вычислить магнитную ин дукцию поля, созданного элементом тока Id на расстоянии от него:

dB = , (5)

т.е. индукция магнитного поля, создаваемого элементом тока Id точке А, (см. рис. 3), на расстоянии r от него, пропорциональна величине элемента тока и синусу угла a, равного углу между направлениями элемента тока Id и , а также обратно пропорциональна квадрату расстояния между ними; Гн / м - магнитная постоянная.

Закон Био - Савара - Лапласа в векторной форме имеет вид: d = . (6)

Закон Био - Савара - Лапласа позволяет вычислить магнитную индукцию поля любых систем токов, используя принцип суперпозиции магнитных поля = . (7)

Применим закон Био - Савара - Лапласа и принцип суперпозиции (7) к расчету магнит ных полей следующих токов:

ЗАКОН АМПЕРА (ФИЗИКА СТР. 209).

МАГНИТОСТАТИКА В ВАКУУМЕ.

Магнитоста́тика — раздел классической электродинамики, изучающий взаимодействие постоянных токов посредством создаваемого ими постоянного магнитного поля и способы расчета магнитного поля в этом случае. Под случаем магнитостатики или приближением магнитостатики понимают выполнение этих условий (постоянства токов и полей — или достаточно медленное их изменение со временем), чтобы можно было пользоваться методами магнитостатики в качестве практически точных или хотя бы приближенных. Магнитостатика вместе сэлектростатикой представляют собой частный случай (или приближение) классической электродинамики; их можно использовать совместно и независимо (расчет электрического и магнитного полей в этом случае не имеет взаимозависимостей — в отличие от общего электродинамического случая).

Все основные уравнения магнитостатики линейны^[1] (как и классической электродинамики вообще, частным случаем которой магнитостатика является). Это подразумевает важную роль в магнитостатике (тоже как и во всей электродинамике) принципа суперпозиции.

· Принцип суперпозиции для магнитостатики может быть сформулирован так: Магнитное поле, создаваемое несколькими токами, есть векторная сумма полей, которые бы создавались каждым из этих токов по отдельности.

Этот принцип одинаково формулируется и в принципе одинаково используется для вектора магнитной индукции и для векторного потенциала и применяется при расчетах повсеместно. Особенно очевидным и прямым образом это проявляется, когда при применении закона Био — Савара (см. ниже) для расчета магнитного поля производится суммирование (интегрирование) бесконечно малых вкладов , создаваемых каждым бесконечно малым элементом тока, текущих в разных точках пространства (точно так же и при применении варианта этого закона для векторного потенциала).

Основные уравнения, используемые в магнитостатике^[2]:

· Закон Био — Савара — Лапласа (величина магнитного поля, генерируемого в данной точке элементом тока)

· Теорема о циркуляции магнитного поля

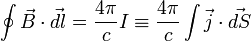
· она же в дифференциальной форме:

· Выражение для силы Лоренца (силы, с которой на движущуюся заряженную частицу действует магнитное поле)

· Выражение для силы Ампера (силы, с которой на элемент тока действует магнитное поле)

(уравнения выше записаны в гауссовой системе единиц); в других системах единиц эти формулы отличаются только постоянными коэффициентами, например:

в системе СИ [показать]

Здесь — вектор магнитной индукции, I — сила тока в проводнике (а в теореме о циркуляции — суммарный ток через поверхность), — элемент проводника (в теореме о циркуляции — элемент контура интегрирования), — радиус-вектор, проведённый из элемента тока в точку, в которой определяется магнитное поле, — плотность тока, —величина заряда и скорость заряженной частицы.

· Для расчёта магнитного поля в магнитостатике можно пользоваться (и часто это весьма удобно) понятием магнитного заряда, делающим аналогию магнитостатики с электростатикой более детальной и позволяющим применять в магнитостатике формулы, аналогичные формулам электростатики — но не для электрического, а для магнитного поля. Обычно (за исключением случая теоретического рассмотрения гипотетических магнитных монополей) подразумевается лишь чисто формальное использование, так как в реальности магнитные заряды не обнаружены. Такое формальное использование (фиктивных) магнитных зарядов возможно благодаря теореме эквивалентности поля магнитных зарядов и поля постоянных электрических токов. Фиктивные магнитные заряды можно использовать при решении разных задач как в качестве источников магнитного поля (например, магнитом или катушкой), так и для определения действия внешних магнитных полей на магнитное тело (магнит, катушку).

Уравнения магнитостатики в среде

Уравнения «для вакуума», приведенные в начале статьи, являются наиболее фундаментальными и простыми (в принципе) уравнениями магнитостатики.

Однако если речь идет о вычислении магнитного поля в среде магнетика, более удобными для практических вычислений, а до некоторой степени и в теоретическом плане, являются менее фундаментальные, однако хорошо приспособленные к этой ситуации, так называемые уравнения для среды (или в среде).

· Говоря о терминологии, следует заметить, что термины уравнения для вакуума и уравнения для среды можно считать в заметной мере условными^[3], однако эта терминология имеет довольно ясное оправдание (см. предыдущее примечание); кроме того, она достаточно устоявшаяся и поэтому не приводит к путанице.

Итак, уравнения для среды используются в магнитостатике для того, чтобы исследовать магнитное поле в случае, когда всё пространство или некоторые его области заполнено магнитной средой (магнетиками). Подразумевается обычно, что среда рассматривается макроскопически (то есть микроскопические поля — поля на атомных масштабах — усредняются, атомные, молекулярные токи и магнитные моменты также рассматриваются только в их совокупности). На микроскопическом уровне действуют^[4] фундаментальные уравнения для вакуума, описанные в статье выше, поэтому в контексте исследования в среде уравнения для ваккма называются также микроскопическими уравнениями в противоположность самим макроскопическим уравнениям для поля в среде.

Формулы для действия поля на движущийся заряд (силы Лоренца) или на ток (силы Ампера) для случая магнитных сред сохраняются полностью неизменными, такими же, как и для вакуума.

Что касается остальных уравнений, они претерпевают для среды определенные изменения по сравнению с вакуумом (имеются в виду, конечно, макроскопические уравнения, микроскопические остаются теми же, что и для вакуума).

В принципе, можно вводить эти изменения по-разному^[5], но весьма общий, традиционный и удобный подход, являющийся общепринятым и стандартным^[6]: записать уравнения с использованием вспомогательной физической величины напряженность магнитного поля , специально вводимой в этом случае.

, где

— в системе СИ,

— в системе СГС.

· Здесь — вектор намагниченности, характеризующий магнитную поляризацию среды.

Смысл её введения состоит в том, что с её помощью можно переписать все основные уравнения в виде, очень похожем на тот, что имеют фундаментальные уравнения (для вакуума), а всё касающееся реальной среды поместить по возможности в отдельное уравнение, что позволяет лучше логически структурировать задачу. В сравнительно простых, но важных случаях, к которым относится и практически вся магнитостатика, это удается сделать настолько хорошо, что, в принципе, действительно всё, касающееся конкретной среды, оказывается полностью спрятано в единственную зависимость — зависимость намагниченности от намагничивающего поля (то есть, в принципе, в одну-единственную формулу)^[7]вида (для случая ферромагнетиков, если требовать точности описания, несколько сложнее, но ненамного).

При этом, что также ценно, уравнения для вакуума становятся частным случаем уравнений для среды (случаем среды с всегда нулевой намагниченностью).

· В простейшем, но практически важном случае линейного^[8] отклика среды на намагничивающее поле, просто пропорционально , а если среда изотропна по своим магнитным свойствам, то это сводится просто к умножению на число:

 

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: