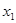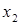|
Корреляционно-регрессионный анализ
|
|
|
|
Корреляционный и регрессионный методы решают две основные задачи:
1. Определение с помощью уравнений регрессии аналитической формы связи между вариацией признаков х и у;
2. Установление меры тесноты связи между признаками (в какой мере вариация х обусловливает вариацию у).
Путем построения и анализа регрессионных моделей можно ответить на вопрос, как каждый фактор влияет на изучаемое явление. Корреляционный и регрессионный методы дают возможность количественно исследовать влияние факторов на изучаемое явление. Современные статистики широко используют метод корреляции. Он выступает как источник теоретических знаний. Между тем применение его без заранее обусловленной цели и качественного анализа нередко приводит к ошибочным выводам.
Для того чтобы корреляционный метод способствовал изучению сущности явлений, необходимо, чтобы исследователь владел не только этим методом, но и предметом своего исследования.
Понятие корреляционной зависимости является частным случаем более общего понятия – зависимости стохастической. Переменная у находится в стохастической зависимости от х, если каждому значению х соответствует ряд распределения у и с изменением х эти ряды закономерно изменяются. Если же они не изменяются или изменяются случайно, то у стохастически не зависит от х.
Основная задача изучения корреляционных связей состоит в отыскании причин исследуемого явления, события, факта. Факторный признак выступает как признак-причина, а результативный – как признак-следствие.
Корреляционный метод анализа включает в себя несколько этапов:
1. Постановка задачи и выбор факторных и результативных признаков;
|
|
|
2. Сбор статистического материала, его проверка;
3. Предварительное изучение взаимосвязей с помощью графиков и аналитических группировок;
4. Изучение парных зависимостей;
5. Исследование многофакторной зависимости;
6. Оценка результатов исследования, пояснение и анализ.
Степень тесноты связи характеризуется количественными оценками, а направление связи знаками у коэффициента корреляции (таблица 11).
Таблица 11. Количественные критерии оценки тесноты связи.
| Величина коэффициента корреляции | Характер связи |
| До |±0,3| | Практически отсутствует |
| От |±0,3| до |±0,5| | Слабая |
| От |±0,5| до |±0,7| | Средняя |
| Свыше |±0,7| | Сильная (высокая) |
Для начала изучим связь между затратами на оплату труда и себестоимостью. Значение факторного признака - затраты на оплату труда ( ) располагается по ранжиру (таблица 12), себестоимость – y.
) располагается по ранжиру (таблица 12), себестоимость – y.
Таблица 12. Ранжированный ряд по затратам
|
| y | Год |
| 7,73 | 68,56 | 1992 |
| 8,40 | 71,23 | 1993 |
| 9,56 | 75,02 | 1994 |
| 12,56 | 530,11 | 1998 |
| 12,84 | 186,63 | 1995 |
| 13,41 | 246,41 | 1996 |
| 14,24 | 391,22 | 1997 |
| 14,26 | 484,14 | 1999 |
| 15,38 | 342,23 | 2000 |
| 18,91 | 676,77 | 2001 |
В среднем наблюдается прямолинейная прямая зависимость, т.е. увеличение затрат на заработную плату приводит к увеличению себестоимости.
Результативный и факторный признаки изменяются одинаково, значит, мы имеем дело с линейной связью.
Далее строим корреляционное поле, приведенное на рисунке 1, для определения направления и аналитического выражения связи между  и y.
и y.
На оси абсцисс наносим значения факторного признака ( ), а на оси ординат – результативного (y), а по данным таблицы 12 все единицы, обладающие определенными значениями
), а на оси ординат – результативного (y), а по данным таблицы 12 все единицы, обладающие определенными значениями  и y.
и y.
Рис.1. Связь между затратами на заработную плату и себестоимостью яйца

Соединив полученные на пересечении  и y точки прямыми линиями, получим статистическую ломанную регрессии (рис.1). Ломанная позволяет судить о форме связи, об аналитическом ее выражении.
и y точки прямыми линиями, получим статистическую ломанную регрессии (рис.1). Ломанная позволяет судить о форме связи, об аналитическом ее выражении.
|
|
|
Корреляционное поле на рис.1 показывает прямолинейную и прямую связь между затратами на заработную плату и себестоимостью яиц. Аналитически связь между факторными и результативными признаками описывается уравнением прямой  .
.
Для определения параметров  и
и  в уравнении прямой данные приводятся в таблице 13.
в уравнении прямой данные приводятся в таблице 13.
Таблица 13 Расчеты параметров уравнения
| Год | Затраты на оплату труда, р. | Себестоимость, р. |
|
|
| Для изучения связи | |

| y | Ранжир по фактору | y=-268,28+ | ||||
| 1992 | 7,73 | 68,56 | 59,75 | 4700,47 | 529,97 | 7,73 | 73,93 |
| 1993 | 8,4 | 71,23 | 70,56 | 5073,71 | 598,33 | 8,40 | 103,59 |
| 1994 | 9,56 | 75,02 | 91,39 | 5628,00 | 717,19 | 9,56 | 154,94 |
| 1995 | 12,84 | 186,63 | 164,87 | 34830,76 | 2396,33 | 12,56 | 287,75 |
| 1996 | 13,41 | 246,41 | 179,83 | 60717,89 | 3304,36 | 12,84 | 300,15 |
| 1997 | 14,24 | 391,22 | 202,78 | 153053,09 | 5570,97 | 13,41 | 325,38 |
| 1998 | 12,56 | 530,11 | 157,75 | 281016,61 | 6658,18 | 14,24 | 362,12 |
| 1999 | 14,26 | 484,14 | 203,35 | 234391,54 | 6903,84 | 14,26 | 363,01 |
| 2000 | 15,38 | 342,23 | 236,54 | 117121,37 | 5263,50 | 15,38 | 412,59 |
| 2001 | 18,91 | 676,77 | 357,59 | 458017,63 | 12797,72 | 18,91 | 568,87 |
| Всего | 127,29 | 3072,32 | 1724,41 | 1354551,08 | 44740,39 | 127,29 | 2952,33 |
Определим параметры  и
и  , для этого необходимо решить систему уравнений относительно
, для этого необходимо решить систему уравнений относительно  и
и  :
:

Подставляем данные таблицы 13:

Решая эту систему уравнений, находим, что  и
и  , следовательно
, следовательно 
Коэффициент регрессии  , следовательно, каждый рубль затрат на заработную плату повышает себестоимость яиц (в среднем) на 44,27р.
, следовательно, каждый рубль затрат на заработную плату повышает себестоимость яиц (в среднем) на 44,27р.
По данным таблицы 13 определим частный коэффициент детерминации
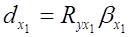 , где
, где  - это частный коэффициент корреляции,
- это частный коэффициент корреляции,
 - бета-коэффициент.
- бета-коэффициент.
 ;
;  ;
;  ;
;
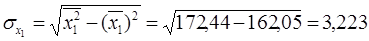 ;
;
 ;
;
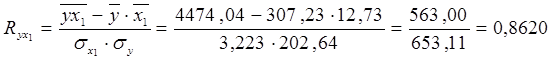 ;
;
 ;
;
 .
.
Это свидетельствует о том, что 60,68% вариации себестоимости яиц объясняется вариацией затрат на заработную плату.
Связь между затратами на заработную плату и себестоимостью проявилась сильная и прямая.
Далее в такой же последовательности рассмотрим зависимость себестоимости яиц (y) от продуктивности ( ).
).
По этим данным в таблице 14 приводятся параллельные данные.
Таблица 14. Ранжированный ряд по урожайности картофеля
|
| y | Год |
| 258 | 68,56 | 1992 |
| 265 | 186,63 | 1995 |
| 265 | 75,02 | 1994 |
| 267 | 71,23 | 1993 |
| 269 | 246,41 | 1996 |
| 319 | 391,22 | 1997 |
| 323 | 676,77 | 2001 |
| 331 | 530,11 | 1998 |
| 333 | 342,23 | 2000 |
| 339 | 484,14 | 1999 |
Связь между себестоимостью и продуктивностью проявляется по прямой.
Проявление связи показано графическим методом на рис.2.
Рис.2. Связь между себестоимостью яиц и продуктивностью
|
|
|

Соединив полученные на пересечении  и y точки прямыми линиями, получим статистическую ломанную. Из графика видно, что связь между факторным и результативным факторами описывается уравнением прямой
и y точки прямыми линиями, получим статистическую ломанную. Из графика видно, что связь между факторным и результативным факторами описывается уравнением прямой 
Для определения параметров  и
и  в уравнении прямой данные приводятся в таблице 15.
в уравнении прямой данные приводятся в таблице 15.
Таблица 15. Расчетная таблица для изучения связи
между себестоимостью яиц и продуктивностью.
| Год | Продуктивность. шт. | Себестоимость, р. |
|
|
| Для изучения связи | ||
|
| y | Ранжир по фактору | y=-1596,56+ +6,41 | |||||
| 1992 | 258 | 68,56 | 66365,09 | 4700,47 | 17662,03 | 258 | 54,75 | |
| 1993 | 267 | 71,23 | 71346,36 | 5073,71 | 19026,06 | 267 | 115,60 | |
| 1994 | 265 | 75,02 | 70437,79 | 5628,00 | 19910,40 | 265 | 104,66 | |
| 1995 | 265 | 186,63 | 70050,84 | 34830,76 | 49395,58 | 265 | 99,98 | |
| 1996 | 269 | 246,41 | 72191,93 | 60717,89 | 66206,81 | 269 | 125,71 | |
| 1997 | 319 | 391,22 | 101545,51 | 153053,09 | 124666,97 | 319 | 446,06 | |
| 1998 | 331 | 530,11 | 109401,98 | 281016,61 | 175339,03 | 331 | 523,61 | |
| 1999 | 339 | 484,14 | 115046,09 | 234391,54 | 164212,76 | 339 | 577,61 | |
| 2000 | 333 | 342,23 | 110775,51 | 117121,37 | 113904,26 | 333 | 536,88 | |
| 2001 | 323 | 676,77 | 104284,16 | 458017,63 | 218549,73 | 323 | 473,43 | |
| Всего | 2968 | 3072,3 | 891445,26 | 1354551,08 | 968873,62 | 2968 | 3058,29 | |
Определим параметры  и
и  , для этого необходимо решить систему уравнений относительно
, для этого необходимо решить систему уравнений относительно  и
и  :
:

Подставляем данные таблицы 15:

Решая эту систему уравнений, находим, что 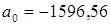 и
и  , следовательно
, следовательно 
Коэффициент регрессии  , следовательно, каждый яйцо продуктивности повышает себестоимость яиц (в среднем) на 6,41р.
, следовательно, каждый яйцо продуктивности повышает себестоимость яиц (в среднем) на 6,41р.
По данным таблицы 15 определим частный коэффициент детерминации
 , где
, где  - это частный коэффициент корреляции,
- это частный коэффициент корреляции,
 - бета-коэффициент.
- бета-коэффициент.
 ;
; 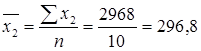 ;
;
 ;
;
Из предыдущего пункта нам уже известно, что  и
и 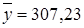 ;
;
Итак,  ;
;
 ;
;
 .
.
Это свидетельствует о том, что 88,99% вариации себестоимости яиц объясняется вариацией продуктивности кур.
Связь между продуктивностью и себестоимостью проявилась сильная и прямая.
Связь между тремя признаками ( ,
,  и y) будем рассматривать множественной корреляцией и регрессией.
и y) будем рассматривать множественной корреляцией и регрессией.
Практика показывает, что основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации. Поэтому и мы для построения нашего многофакторного модуля взаимосвязи будем использовать линейную модель: 
Для определения параметров 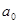 ,
,  и
и 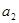 необходимо решить уравнения:
необходимо решить уравнения:
|
|
|
 ;
;
 ;
;
 .
.
Для удобства решения запишем все необходимые данные в таблицу 16.
Таблица 16. Расчетная таблица для изучения множественной корреляции.
| Год | Затраты на оплату труда, р. | Продуктивность, шт. | Себестоимость, р. |
|
|
|
|
|
|
|
| y | ||||||
| 1992 | 7,73 | 258 | 68,56 | 59,75 | 66564 | 529,97 | 17688,48 | 1994,34 |
| 1993 | 8,4 | 267 | 71,23 | 70,56 | 71289 | 598,33 | 19018,41 | 2242,80 |
| 1994 | 9,56 | 265 | 75,02 | 91,39 | 70225 | 717,19 | 19880,30 | 2533,40 |
| 1995 | 12,84 | 265 | 186,63 | 164,87 | 70225 | 2396,33 | 49456,95 | 3402,60 |
| 1996 | 13,41 | 269 | 246,41 | 179,83 | 72361 | 3304,36 | 66284,29 | 3607,29 |
| 1997 | 14,24 | 319 | 391,22 | 202,78 | 101761 | 5570,97 | 124799,18 | 4542,56 |
| 1998 | 12,56 | 331 | 530,11 | 157,75 | 109561 | 6658,18 | 175466,41 | 4157,36 |
| 1999 | 14,26 | 339 | 484,14 | 203,35 | 114921 | 6903,84 | 164123,46 | 4834,14 |
| 2000 | 15,38 | 333 | 342,23 | 236,54 | 110889 | 5263,50 | 113962,59 | 5121,54 |
| 2001 | 18,91 | 323 | 676,77 | 357,59 | 104329 | 12797,72 | 218596,71 | 6107,93 |
| Всего | 127,29 | 2969 | 3072,32 | 1724,41 | 892125 | 44740,39 | 969276,78 | 38543,96 |




Уравнение множественной регрессии:

Расчеты показывают, что с увеличением затрат на заработную плату на 1 рубль себестоимость увеличивается на 54,18р., а также, что с увеличением продуктивности на 1 яйцо себестоимость повышается на 5,41р.
Совокупный множественный коэффициент корреляции рассчитывается по формуле:

Связь проявилась сильная, т.е. отклонение себестоимости яиц от средней по совокупности зависит от затрат на заработную плату и продуктивности на 87,09%.
На основе коэффициентов регрессии ( и
и  ) нельзя сказать, какой из факторных признаков оказывает наибольшее влияние на результативный признак. Чтобы судить о сравнительной силе влияния отдельных факторов, вычислим Q - коэффициент, который вычисляется по формуле:
) нельзя сказать, какой из факторных признаков оказывает наибольшее влияние на результативный признак. Чтобы судить о сравнительной силе влияния отдельных факторов, вычислим Q - коэффициент, который вычисляется по формуле:
 , где
, где
 - коэффициент вариации, соответствующего факторного признака;
- коэффициент вариации, соответствующего факторного признака;
 - коэффициент эластичности.
- коэффициент эластичности.
 ;
;

Это означает, что при увеличении затрат на заработную плату на 1% себестоимость увеличивается на 2,24%, а при росте продуктивности на 1% себестоимость увеличивается на 5,23%.
 ; ;
| 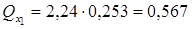 ; ;
|

|  . .
|
Из двух изучаемых факторов наиболее существенное влияние на вариацию себестоимости по районам оказывает фактор  - продуктивность.
- продуктивность.
Ряды динамики
Рядом динамики называется временная последовательность значений статистических показателей.
Ряд динамики состоит из двух элементов: моментов времени (обычно дат) или периодов времени (годы, кварталы, месяцы), к которым относятся статистические данные, и самих данных, называемых уровнями ряда. Оба элемента – время и уровень – называются членами ряда динамики.
Для правильного анализа динамических рядов необходимо знать их виды, которые выделяются при группировке элементов ряда по разным признакам.
По времени, отражаемому в динамических рядах, они разделяются на моментные и интервальные.
|
|
|
В моментных рядах динамики уровни ряда выражают величину явления на определенную дату. В них время обозначает момент, к которому относится каждый уровень ряда. Уровни моментных рядов динамики суммировать не имеет смысла, поскольку суммирование будет включать одну и ту же величину несколько раз, но разность уровней имеет определенный смысл.
В интервальных рядах уровни ряда выражают размеры явления за определенный промежуток времени. Отличительной особенностью интервальных рядов динамики абсолютных величин является возможность суммировать уровни следующих друг за другом периодов, поскольку их можно рассматривать как итог за более длительный период времени.
По способу выражения уровней рядов динамики они могут быть рядами абсолютных, средних и относительных величин.
При изучении динамики социально-экономических явлений используют некоторые статистические характеристики, которые позволяют измерить изменение явлений во времени.
Большинство статистических характеристик основано на абсолютном или относительном сравнении уровней динамических рядов показателей динамики: абсолютный прирост, темпы роста и прироста, абсолютное значение одного процента прироста. Сравниваемый уровень называется текущим, а уровень, с которым производится сравнение, базисным. За базисный уровень часто принимается либо предыдущий уровень, либо начальный в данном динамическом ряду. Если производится сравнение каждого уровня с предыдущим, то получаются цепные показатели динамики. Если каждый уровень сравнивается с начальным или каким-либо другим, принятым за базу сравнения, то получаются базисные показатели.
Выбор базы сравнения должен быть обоснован исторически и экономически, так чтобы база отражала определенный этап развития явления. Иногда за базу сравнения принимается средний уровень какого-либо предшествующего периода.
Ряды динамики могут быть с равностоящими (по времени) уровнями и не равностоящими.
Чтобы выделить специфику развития явления за отдельные периоды времени определяют абсолютные и относительные показатели ряда динамики (абсолютный прирост, темпы роста, темпы прироста, абсолютное значение одного процента прироста) цепным или базисным способами.
Абсолютный рост (снижение) исчисляются как разность сравниваемых уровней:
  или или
|  , где , где
|
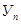 - уровень текущего n-ого периода;
- уровень текущего n-ого периода;
 - уровень предшествующего периода;
- уровень предшествующего периода;
 - уровень базисного периода (в нашем случае за этот уровень взята средняя величина урожайности картофеля за весь период).
- уровень базисного периода (в нашем случае за этот уровень взята средняя величина урожайности картофеля за весь период).
Интенсивность изменения уровня в динамике определяется отношением уровней и выражается коэффициентом роста (снижения):
 или или
| 
|
Данные коэффициентов характеризуют интенсивность - во сколько раз произошло изменение. А интенсивность изменения в процентах выражается показателем – темп роста (снижения):
 или или
| 
|
Чтобы выразить изменение величины абсолютного прироста (снижения) в процентах, исчисляют показатель темпа прироста (снижения).
 и
и 
Можно определить по схеме:
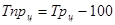 или или
| 
|
Абсолютное значение одного процента прироста:
 или или
| 
|
Средние значения показателей ряда динамики определяют по той или иной формуле в зависимости от его вида и способе получения статистических данных. Если ряд динамики с равностоящими уравнениями во времени расчет среднего уровня изучаемого явления  производится по средней арифметической простой:
производится по средней арифметической простой: 
Средний абсолютный прирост (снижение) определяется по схеме:

Среднегодовой коэффициент роста определяется по средней геометрической: 
Среднегодовой темп роста (снижения): 
Среднегодовой темп прироста: 
Все показатели динамики себестоимости яиц приведены в таблице 17.
Таблица 17. Себестоимость яйца в СХ ОАО «Белореченское»
и показатели динамики
| Год | Себестоимость | Абсолютный прирост | Коэффициент роста | Темп роста | Темп прироста | Значение 1% прироста | ||||
| ц | б | ц | б | ц | б | ц | б | ц | ||
| 1992 | 68,56 | - | -238,67 | - | 0,22 | - | 22,32 | - | -77,68 | - |
| 1993 | 71,23 | 2,67 | -236,00 | 1,04 | 0,23 | 103,89 | 23,18 | 3,89 | -76,82 | 0,69 |
| 1994 | 75,02 | 3,79 | -232,21 | 1,05 | 0,24 | 105,32 | 24,42 | 5,32 | -75,58 | 0,71 |
| 1995 | 186,63 | 111,61 | -120,60 | 2,49 | 0,61 | 248,77 | 60,75 | 148,77 | -39,25 | 0,75 |
| 1996 | 246,41 | 59,78 | -60,82 | 1,32 | 0,80 | 132,03 | 80,20 | 32,03 | -19,80 | 1,87 |
| 1997 | 391,22 | 144,81 | 83,99 | 1,59 | 1,27 | 158,77 | 127,34 | 58,77 | 27,34 | 2,46 |
| 1998 | 530,11 | 138,89 | 222,88 | 1,36 | 1,73 | 135,50 | 172,54 | 35,50 | 72,54 | 3,91 |
| 1999 | 484,14 | -45,97 | 176,91 | 0,91 | 1,58 | 91,33 | 157,58 | -8,67 | 57,58 | 5,30 |
| 2000 | 342,23 | -141,91 | 35,00 | 0,71 | 1,11 | 70,69 | 111,39 | -29,31 | 11,39 | 4,84 |
| 2001 | 676,77 | 334,54 | 369,54 | 1,98 | 2,20 | 197,75 | 220,28 | 97,75 | 120,28 | 3,42 |
| В среднем | 307,23 | 65,58 | - | 1,2897 | - | 128,97 | - | 3,44 | - | 2,40 |
 р.
р.
Для расчета базисных показателей за базу сравнения принимается средняя за 10 лет (307,23р.).
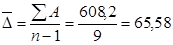 р.;
р.;

Средний темп роста и средний темп прироста:
 ;
;
 .
.
Наблюдается снижение себестоимости, произошедшее в 2000г. по сравнению с 1999г. на 141,91р или 29,31%. Иначе говоря, себестоимость в 2000г. по сравнению с 1999г. составляет 70,69%, т.е. снижение в 0,71 раз. При сравнении с постоянной базой сравнения наибольшее снижение произошло в 1992г, на 238,67р. или на 77,68%.
Максимальное повышение себестоимости произошло в 2001г по сравнению с 2000г и составило 334,54р. или на 97,75%, если сравнивать с постоянной базой сравнения, то максимальное повышение произошло в том же 2001г – на 369,54 или на 120,28%.
При анализе рядов динамики необходимо учесть тенденцию изменения уровня себестоимости за 1992-2001 гг.
Тенденция – это основное направление развития. Основной тенденцией (трендом) называется плавное и устойчивое изменение уровня признака во времени свободное от случайных колебаний.
Наиболее эффективным способом выявления основной тенденции отклонений изучаемых признаков является аналитическое выравнивание. Выбор функции времени  производится на основе анализа характера закономерностей динамики данного признака.
производится на основе анализа характера закономерностей динамики данного признака.
С помощью графического метода, приведенного на рис.3, рассматривается характер закономерностей изменения уровня себестоимости яиц.
В системе координат на оси абсцисс наносятся временные интервалы, а на оси ординат - уровни себестоимости.
Рис.3. Динамика себестоимости яиц
в СХ ОАО «Белореченское» за 1992-2001гг.

На рис.3 статистическая ломаная показывает, что за 1992-2001 гг. себестоимость яиц (в среднем) имеет тенденцию к повышению. Для выравнивания используем уравнение прямой:  ,
,
Чтобы определить параметры уравнения  ,
,  составим систему уравнений:
составим систему уравнений:

Для решения данной системы приводится расчетная таблица 18.
Таблица 18. Расчетная таблица для выравнивания ряда динамики
себестоимости яиц
| Год | Исходная информация | Расчетная информация | Выровненная себестоимость, р. |
|
| ||
| Себестоимость, р. | Номер года | ||||||
|
| 
|
| 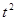
| 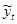
| |||
| 1992 | 68,56 | 0 | 0 | 0 | 13,02 | 55,54 | 3084,692 |
| 1993 | 71,23 | 1 | 71,23 | 1 | 78,4 | -7,17 | 51,4089 |
| 1994 | 75,02 | 2 | 150,04 | 4 | 143,78 | -68,76 | 4727,938 |
| 1995 | 186,63 | 3 | 559,89 | 9 | 209,16 | -22,53 | 507,6009 |
| 1996 | 246,41 | 4 | 985,64 | 16 | 274,54 | -28,13 | 791,2969 |
| 1997 | 391,22 | 5 | 1956,1 | 25 | 339,92 | 51,30 | 2631,69 |
| 1998 | 530,11 | 6 | 3180,66 | 36 | 405,3 | 124,81 | 15577,54 |
| 1999 | 484,14 | 7 | 3388,98 | 49 | 470,68 | 13,46 | 181,1716 |
| 2000 | 342,23 | 8 | 2737,84 | 64 | 536,06 | -193,83 | 37570,07 |
| 2001 | 676,77 | 9 | 6090,93 | 81 | 601,44 | 75,33 | 5674,609 |
| Всего | 3072,32 | 45 | 19121,31 | 285 | 3072,3 |
| 70798,01 |
 , откуда
, откуда  ,
, 
Уравнение для выравнивания выглядит следующим образом:
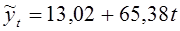
Кривая на рис.3 показывает, что себестоимость яиц в 1992-2001гг. ежегодно увеличивалась (в среднем) на 65,38р.
Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровень ряда динамики, а колебание уровней около тренда служит мерой воздействия остаточных факторов.
Её можно измерить по формуле среднего квадратического отклонения:

В среднем колебания себестоимости яиц по годам от среднего уровня составляет ±84,14р. или 27,39% [(84,14:307,23)·100%].
Индексный анализ
|
|
|