 |
Дифференциальное исчисление функции одной переменной.
|
|
|
|
Задача 14
Найти производные первого порядка заданных функций:
14.1. 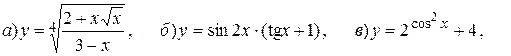
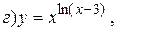

14.2. 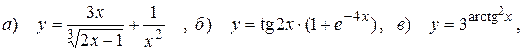
 ,
, 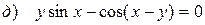
14.3. 
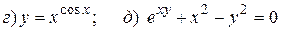
14.4. 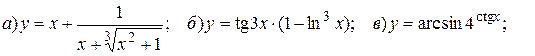
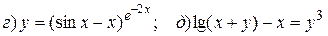
14.5. 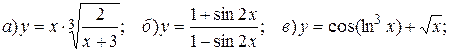
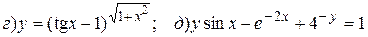
14.6. 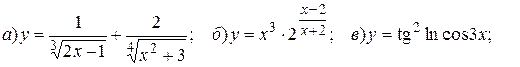
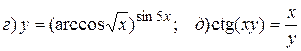
14.7. 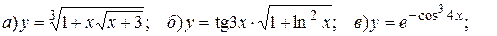
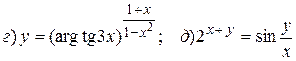
14.8. 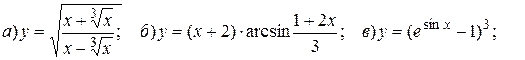
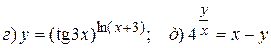
14.9. 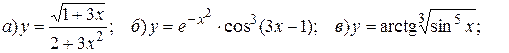
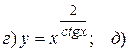

14.10. 
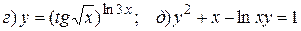
Задача 15
Найти 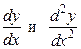 для заданных функций:
для заданных функций:
15.1. 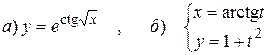
15.2. 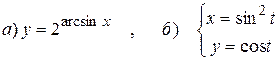
15.3. 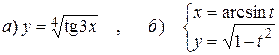
15.4. 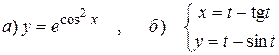
15.5. 
15.6. 
15.7. 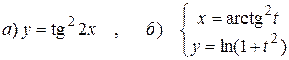
15.8. 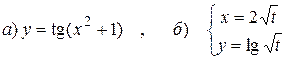
15.9. 
15.10. 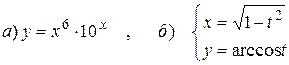
Задача 16
Используя геометрический или физический смысл производной, решить задачу:
16.1. а) В какой точке касательная к параболе у = – х 2 + 7 х – 10перпендикулярна прямой х + у -1 = 0? Составить уравнение касательной. Сделать чертеж.
б) Колесо вращается так, что угол поворота пропорционален квадрату времени. Первый оборот был сделан колесом за время Т = 8 сек. Найти угловую скорость w в момент t = 32 сек после начала движения.
16.2. а) При каком значении независимой переменной касательные к кривым у = х 2 и у = х 3 параллельны? Найти уравнения этих касательных. Сделать чертеж.
б) Тело массой т = 4 двигается прямолинейно по закону X = t2+ t+ 1. Определить кинетическую энергию тела в момент времени t = 5.
16.3. а) Под каким углом график функции у =  пересекает прямую х = 2.
пересекает прямую х = 2.
б) Радиус шара изменяется со скоростью v. С какой скоростью изменяется объем и поверхность шара?
16.4. а) Под каким углом пересекаются кривые х 2 – у 2 = 5и 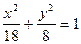 ? Указание: под углом между кривыми понимают угол между касательными к этим кривым в точке их пересечения.
? Указание: под углом между кривыми понимают угол между касательными к этим кривым в точке их пересечения.
б) Угол j, на который поворачивается колесо за t сек., равен j 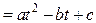 , где
, где 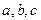 - положительные константы. Найти угловую скорость w движения колеса. Через сколько времени от начала движения угловая скорость будет равна нулю?
- положительные константы. Найти угловую скорость w движения колеса. Через сколько времени от начала движения угловая скорость будет равна нулю?
16.5. а) Показать, что отрезок касательной к астроиде  , заключенный между осями координат, имеет постоянную длину, равную
, заключенный между осями координат, имеет постоянную длину, равную 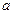 .
.
б) В какой точке эллипса 16 х2 + 9 у 2 = 400 ордината убывает с той же скоростью, с какой возрастает абсцисса?
|
|
|
16.6. а) Какой угол образует с прямой у = 2 х - 3 касательная к параболе у = х 2 - 3 х+ 5, проведенная в точке (2, 3)? Найти уравнение этой касательной. Сделать чертеж.
б) Барометрическое давление Ризменяется с высотой h по закону  , где Р0 - нормальное давление, с – некоторая постоянная. На высоте 5540 м давление равно половине нормального. Установите зависимость скорости изменения давления от высоты.
, где Р0 - нормальное давление, с – некоторая постоянная. На высоте 5540 м давление равно половине нормального. Установите зависимость скорости изменения давления от высоты.
16.7. а) Найти уравнение касательной и нормали в точке (2; 2) к кривой, заданной параметрически уравнениями 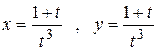 .
.
б) По оси абсцисс двигаются две точки, имеющие законы движения х= 100 +5t и х = 0,5 t, где t >0. С какой скоростью удаляются точки друг от друга в момент встречи?
16.8. а) Найти уравнение касательной к кривой у = х 2 + 2 х - 1 в точке её пересечения с параболой у = 2 х 2. Сделать чертеж.
б) Показать, что если тело движется по закону S = a e-t + b e-t , то его ускорение численно равно пройденному пути.
16.9. а) Найти координаты точки, в которой касательная к параболе у= х 2 + 3 х - 10образует угол 1350 с положительным направлением оси ОХ. Найти уравнение этой касательной. Сделать чертеж.
б) Точка двигается прямолинейно по закону s = t 3 - 16 t 2 + 64 t. Определить: 1) в какие моменты времени точка находилась в начале координат; 2) в какие моменты времени её скорость была равна нулю?
16.10. а) Написать уравнение касательной к кривой 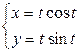 в точке (-
в точке (-  , 0).
, 0).
б) Точка двигается по гиперболе  так, что ее абсцисса растет равномерно со скоростью 1 единица в секунду. С какой скоростью изменяется ее ордината, когда точка проходит положение (5;2)?
так, что ее абсцисса растет равномерно со скоростью 1 единица в секунду. С какой скоростью изменяется ее ордината, когда точка проходит положение (5;2)?
Задача 17
Исследовать функцию и построить ее график:
17.1. 
| 17.2. у = 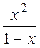
|
17.3. у = 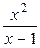 . .
| 17.4. 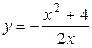
|
17.5. 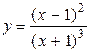
| 17.6. 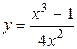
|
17.7. 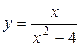
| 17.8. 
|
17.9. 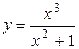
| 17.10. 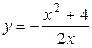
|
Функции нескольких переменных
Задача 18.
Найти область определения функции. Сделать чертеж.
18.1. а) 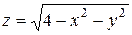 ; б)
; б) 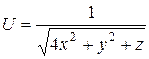 .
.
18.2.. а)  ; б)
; б) 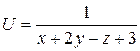 .
.
18.3.. а)  ; б)
; б) 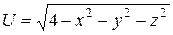 .
.
18.4. а) 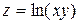 ; б)
; б) 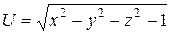 .
.
18.5. а) 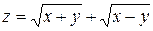 ; б)
; б)  .
.
18.6. а) 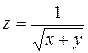 ; б)
; б) 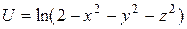 .
.
18.7. а) 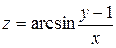 ; б)
; б) 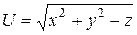 .
.
18.8. а) 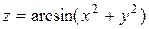 ; б)
; б) 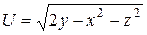 .
.
|
|
|
18.9. а) 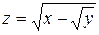 ; б)
; б) 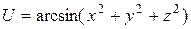
18.10. а) 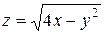 ; б)
; б) 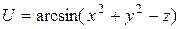 .
.
Задача 19.
Проверить, удовлетворяет ли данная функция 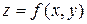 указанному уравнению.
указанному уравнению.
19.1 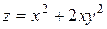 ,
,  .
.
19.2 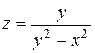 ,
, 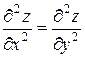 .
.
19.3 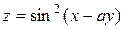 ,
, 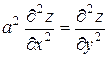 .
.
19.4 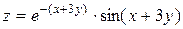 ,
, 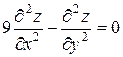 .
.
19.5  ,
, 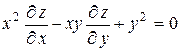 .
.
19.6  ,
, 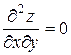 .
.
19.7  ,
, 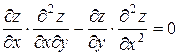 .
.
19.8. 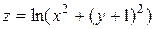 ,
,  .
.
19.9 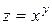 ,
, 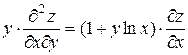 .
.
19.10. 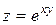 ,
, 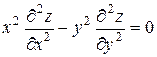
Задача 20.
Линеаризовать функцию 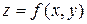 в окрестности точки
в окрестности точки 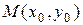 .
.
20.1. 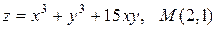 .
.
20.2.  .
.
20.3. 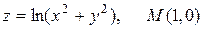 .
.
20.4. 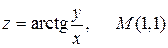 .
.
20.5. 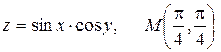 .
.
20.6. 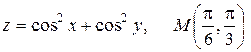
20.7.  .
.
20.8. 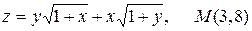 .
.
20.9.  .
.
30.10. 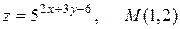 .
.
Задача 21.
Для функции 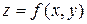 найти:
найти:
а) производную в точке 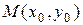 в направлении вектора
в направлении вектора  ;
;
б) градиент в точке 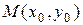 и наибольшую скорость изменения функции в этой точке.
и наибольшую скорость изменения функции в этой точке.
21.1. 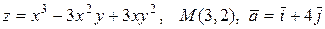 .
.
21.2. 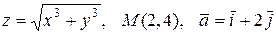 .
.
21.3. 
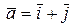 .
.
21.4.. 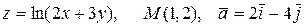 .
.
21.5. 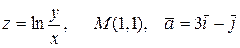 .
.
21.6.  .
.
21.7. 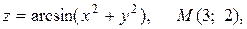
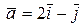 .
.
21.8. 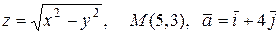 .
.
21.9.  .
.
21.0. 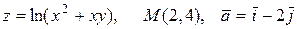 .
.
Задача 22.
Найти экстремум функции 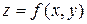 .
.
22.1. 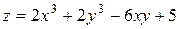 .
.
22.2. 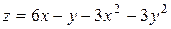 .
.
22.3. 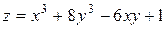 .
.
22.4.  .
.
22.5. 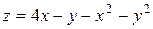 .
.
22.6.  .
.
22.7. 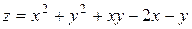 .
.
22.8.  .
.
22.9.  .
.
22.10. 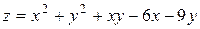 .
.
Задача 23.
Методом наименьших квадратов найти функцию y = f (x) в виде y = ax + b (в нечетных номерах) и y = ax 2 + b (в четных номерах). Экспериментально полученные п значений искомой функции y = f (x) при п значениях аргумента приведены в таблице.
23.1. 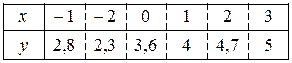
23.2. 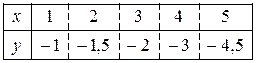
23.3. 
23.4. 
23.5. 
23.6. 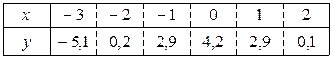
23.7. 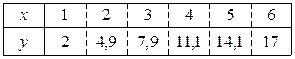
23.8. 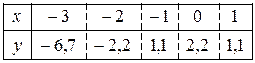
23.9. 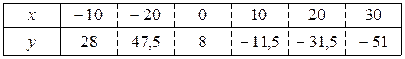
23.10. 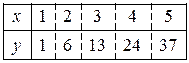
|
|
|


