Главная | Обратная связь | Поможем написать вашу работу!

Параметры-массивы в функциях

Если мы хотим передать в подпрограмму отдельный элемент
массива, то в качестве соответствующего ему формального параметра указывается простая переменная того же типа.

Массивы, так же как и простые переменные, можно передавать в функции в качестве параметров. Так как имя массива – это адрес, то передача массива происходит всегда по адресу.

Рассмотрим, например, функцию, вычисляющую среднее значение элементов массива. Желательно сделать ее так, чтобы в нее можно было передавать массивы любого размера и она всегда правильно вычисляла результат. В языке С++ функции не могут самостоятельно определять размер массива, поэтому он должен быть обязательно одним из параметров.

#include "stdafx.h"

int Sum (int A[], int N)

{

int i, sum;

sum = 0;

for (i = 0; i < N; i ++)

sum += A[i];

return sum/N;

}

void main()

{

int x[5]={1,2,3,4,5},y[3]={11,22,33};

printf("\nsr x=%d sr y=%d\n",

Sum(x,5),Sum(y,3));

}

Обратите внимание, что в заголовке функции размер массива указан отдельно. Нельзя объявлять массив-параметр как A[N], а только как A[] или *A.

Если в функцию передаётся двумерный массив, то описание соответствующего аргумента функции должно содержать количество столбцов; количество строк - несущественно, поскольку фактически передаётся указатель. Например: int Х[ ][5], или Х[5][5].

Рассмотрим пример функции, перемножающей матрицы А и В; результат - матрица С.

const nmax = 10;

void product(int А[][nmax], int В[][nmax],int С[][nmax], int m, int n, int k)

{
/* m - число строк в матрице А;
n - число строк в матрице В (должно быть равно числу столбцов в матрице А);
k - число столбцов в матрице В.
*/
for (int i=0; i< m; i++)
for (int j=0; j< k; j++){
С[i][j]=0;
for (int l=0; l< n; l++)

С[i][j] + = А[i][l]*В[l][j];
}
}

В приведённом примере есть недостаток - здесь заранее фиксируется максимальная размерность матриц. Но использоваться может только часть памяти.

Рекурсия

В теле функции известны все объекты, описанные во внешнем блоке, т.е. все глобальные переменные и имя самой функции.

Таким образом, внутри любой функции можно вызывать любую доступную функцию, в том числе и саму себя. Ситуация, когда функция вызывает саму себя, называется рекурсия.

Рекурсия возможна благодаря тому, что при вызове функции создаются новые экземпляры локальных переменных, которые сохраняются во внутреннем стеке машины. Стек функционирует по принципу LIFO - Last In – First Out (последний вошел – первый вышел).

Переменные помещаются в стек одна за другой и выбираются из стека в обратном порядке.

Обязательным элементом всякого рекурсивного процесса является утверждение, определяющее условие завершения рекурсии. Оно называется опорным условием рекурсии.

Если опорное условие выполняется, то может быть задано некоторое фиксированное значение, заведомо достижимое в ходе вычисления. Это позволит организовать своевременную остановку рекурсивного процесса.

Рассмотрим пример вычисления факториала 5.

, где - это 4!

Т.е 5!=4! 5

Факториал нуля равен 1. Отсюда формула вычисления N-факториала:

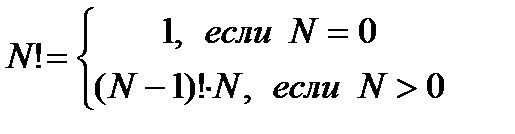
Реализуем вычисление факториала в виде функции:

#include "stdafx.h"

float fact(int n)

{

if (n==0)

return 1;

else

return (fact(n-1)*n);

}

void main()

{

printf("факториал 5=%f\n",fact(5));

}

Примеры программирования задач с использованием подпрограмм

При программировании задач возможны несколько вариантов. Выбор правильного (более эффективного и надежного) варианта зависит от опыта программиста

Задача 1

Даны два вектора: = {х_i}; i = и ={y_i};i = . Вычислить значение: D = , где ; ;

тх, ту - максимальные компоненты векторов и соответственно;

sx, sy - средние значения компонент векторов и соответственно.

Решение:

#include "stdafx.h"

#include <math.h>

float Mod_Otkl (float *a, int n) /* функция для нахождения максимального компонента и среднего значения в любом массиве */

{

float ma, sa, Da;

int i;

ma =-10000;

sa=0;

for (i =0;i<n;i++)

{

if (a[i]>ma) ma= a[i];

sa += a[i];

}

sa = sa/n;

Da= fabs(ma - sa);

return Da;

}

void main()

{ float X[10],Y[10];

int i;

float Dx, Dy, D;

printf("Bведитe массив X:\n");

for (i =0;i<8;i++)

scanf("%f",&X[i]);

printf("Bведитe массив Y:\n");

for (i =0;i<10;i++)

scanf("%f",&Y[i]);

Dx = Mod_Otkl(X, 8); //вызов функции Mod_Otkl для массива X

Dy = Mod_Otkl(Y,10); //вызов функции Mod_Otkl для массива Y

D = Dx/Dy;

printf("D=%f\n",D);

}

Задача 2

Даны две матрицы: А = {a _i _j }₅_x₆ и В = {b _i _j }₄_x₇.

Вычислить разность: С = КА - KB, где КА и KB - количество положительных элементов в матрицах А и В соответственно.

#include "stdafx.h"

int CP(float D[7][7], int m, int n) /* функция для подсчета количества положительных элементов в матрице */

{ int i, j, KD;

KD=0;

for (i=0;i<m;i++)

for (j=0;j<n;j++)

if (D[i][j]>0) KD ++;

return KD;

}

int main()

{

float A[7][7], B[7][7];

int i,j, C;

printf("Введите матрицу А\n");

for (i=0;i<5;i++)

for (j=0;j<6;j++)

scanf("%f",&A[i][j]);

printf("Введите матрицу B\n");

for (i=0;i<4;i++)

for (j=0;j<7;j++)

scanf("%f",&B[i][j]);

C= CP(A, 5,6) - CP(B, 4, 7);

printf("C=%d\n", C);

return 0;

}

Задача 3

На плоскости декартовыми координатами заданы 10 точек:

{x₁,y₁},{x₂,y₂},...,{х₁₀,у₁₀}.

Вывести полярные координаты точки, имеющей наибольший полярный радиус. Вычисление полярных координат одной точки оформить подпрограммой. Расчетные формулы для вычисления полярных координат следующие:

, где а и b - координаты точки.

Решение:

#include "stdafx.h"

#include<math.h>

void PK(float a, float b, float *ro, float *fi) /* функция для расчета полярных координат точки */

{

*ro = sqrt(a*a + b*b);

*fi = atan(b/a);

}

int main()

{

float X[10], Y[10], R[10], F[10];

int i, n;

float max;

printf("Введите абсциссы 10 точек\n");

for (i=0;i<10;i++) scanf("%f",&X[i]);

printf(" Введите ординаты 10 точек\n");

for (i=0;i<10;i++) scanf("%f",&Y[i]);

max = 0;

for (i=0;i<10;i++)

{

PK(X[i],Y[i],&R[i],&F[i]);

if (R[i]>max) // поиск максимального радиуса

{

max =R[i];

n=i;

}

printf("romax=%f fimax=%f\n", R[n],F[n]);

return 0;

}

Задача 4

Для заданных квадратных матриц: A = {a _i _j}₃_x₃ и В = {b_i_j}_4х4 вычислить симметричные матрицы по правилу:

Решение:

#include "stdafx.h"

void SM(float Y[4][4], int n, float X[4][4])

{

int i,j;

for (i=0;i<n;i++)

for (j=i;j<n;j++)

{

X[i][j]=(Y[i][j] + Y[j][i])/2;

X[j][i] =X[i][j];

}

void main()

{

float A[4][4], B[4][4], C[4][4], D[4][4];

int i, j;

printf("Введите матрицу А\n");

for (i=0;i<3;i++)

for (j=0;j<3;j++) scanf("%f",&A[i][j]);

printf("Введите матрицу B\n");

for (i=0;i<4;i++)

for (j=0;j<4;j++) scanf("%f",&B[i][j]);

SM(A, 3,C);

SM(B, 4, D);

printf("Симметричная матрица С\n");

for (i=0;i<3;i++)

{for (j=0;j<3;j++) printf("%8.2f",C[i][j]);

printf("\n");

}

printf("Симметричная матрица D\n");

for (i=0;i<4;i++)

{for (j=0;j<4;j++) printf("%8.2f",D[i][j]);

printf("\n");

}

Текстовые данные

В языке С++ текстовая информация представляется двумя типами данных: с помощью символов и строк - массивов символов.

Символьный тип данных

Значением данных символьного типа является любой символ
из набора всех символов компьютера или его код. Каждому символу соответствует порядковый номер (код) в диапазоне 0..255. Для кодировки символов первой половины диапазона используется код ASCII (американский стандартный код для обмена информацией),
или более современные стандарты в последних версиях языка Си.

При написании программ символьные данные могут быть
представлены либо константами, либо переменными.

Символьная константа представляет собой одиночный
символ, заключенный в апострофы, например:

‘Y’ ‘!’ ‘_’ ‘Д’

Символьная переменная объявляется с помощью ключевого слова char, например:

char cr;

Во внутренней памяти компьютера каждый символ занимаем 1 байт.

⇐ Предыдущая 11 12 13 14 15 161718 19 20 Следующая ⇒

Воспользуйтесь поиском по сайту: