 |
Пример обозначения болта с диаметром резьбы d = 12 мм, с размером под ключ S = 18 мм, длиной 60 мм с крупным шагом резьбы; поле допуска 6g, класс прочности 5.8
|
|
|
|
безпокрытия: Болт Ml2 - 6g х 60. 58 (SI8) ГОСТ 7798-70.
Таблица №21 Подшипники шариковые радиальные однорядные 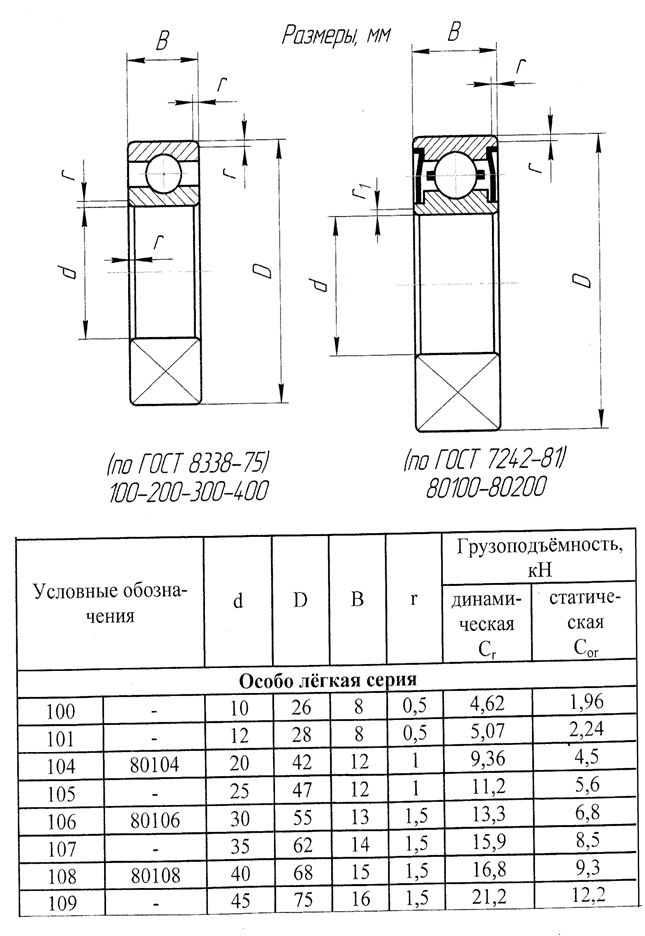
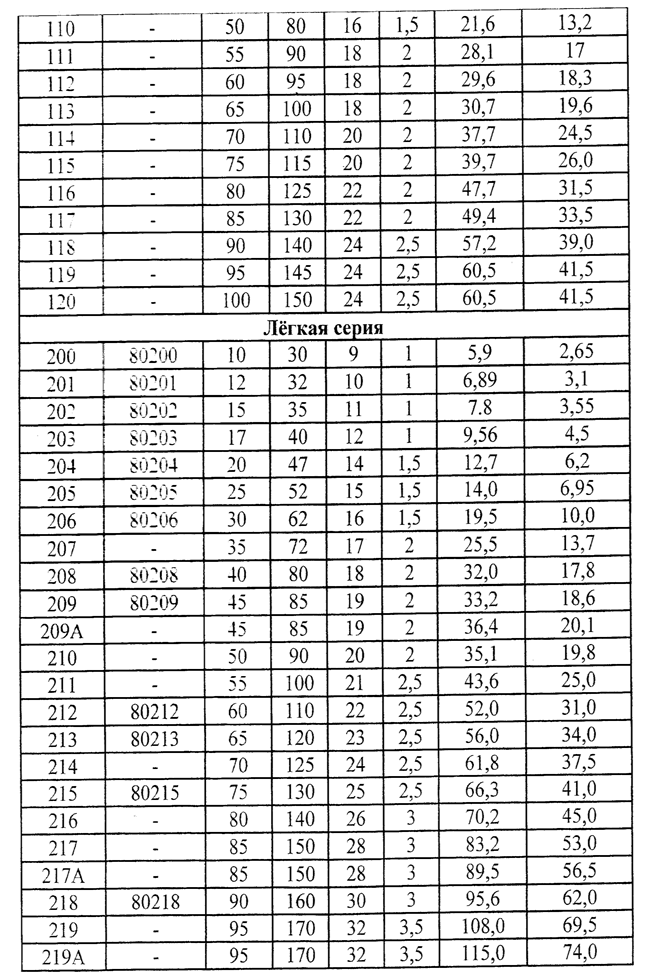
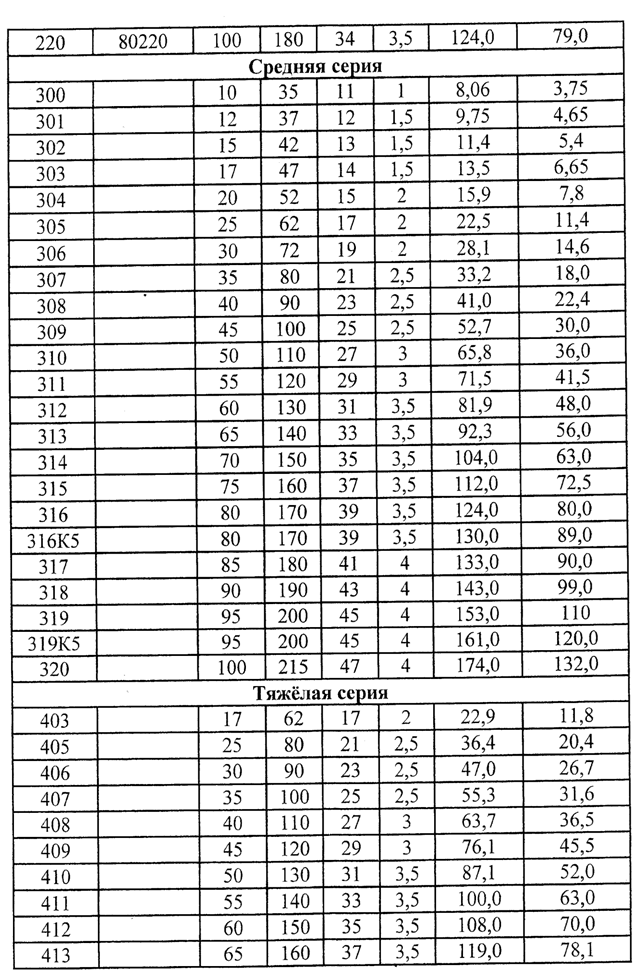
Таблица №22 Рекомендуемые значения вязкости масел при t=50° С
|
Контактное напря-жение sН , МПа | Кинематическая вязкость, ˑ 10-6 м2 /с при окружной скорости v, м/с | ||
| до 2 | от 2 до 5 | св. 5 | |
| До 600 | |||
| Св. 600 до 1000 | |||
Таблица №23 Масла, применяемые для смазывания зубчатых передач при t = 50°С
| Сорт масла | Марка | Кинематическая вязкость, •10-6 м/с |
| Индустриальное | И-12А И-20А И-25А И-30А И-40А И-50А И-70А И-100 А | 10-14 17-23 24-27 28-33 35-45 47-55 65-75 90-118 |
Таблица №24 Пластичные смазочные материалы
| Наименование и марка смазки | ГОСТ | t, °С эксплуатации | t, °С каплепадения |
| Гидратированные кальциевые солидолы | |||
| Солидол С Пресс-солидол С Солидолы жировые, пресс-солидол | 4366 - 76 1033-79 | от -20 до +65 от -30 до +50 от -25 до +65 | 85-105 85-95 75 |
|
| |||
| Многоцелевые | |||
|
| |||
| Литол - 24 | 21150-75 | от -40 до +130 | |
| Морозостойкие(тугоплавкие) | |||
| ЦИАТИМ - 201 ЦИАТИМ - 203 | 6267 - 74 8773 - 73 | от -60 до +90 от -50 до +90 | |
| Натриевые и натриево-кальциевые | |||
| Консталин жировой УТ-1 | 1957-73 | от -20 до +120 | 130-150 |
Рисунок1. График зависимости G=f(аw) 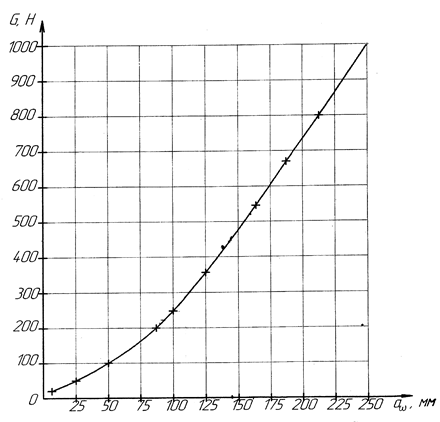
Пример расчетов 
Рассчитать и спроектировать одноступенчатый горизонтальный шевронныйцилиндрический редуктор общего назначения
Исходные данные:
Мощность на выходном валу: P3= 2, 22 кВт Частота вращения выходного вала: n3= 112 об/мин Характер нагрузки: реверсивный
Схема 1-7-2-3
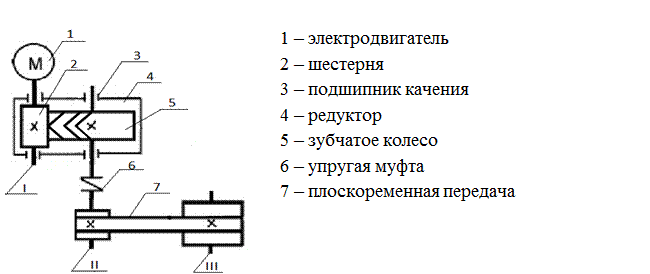 I. Быстроходный вал редуктора II. Тихоходный вал редуктора
I. Быстроходный вал редуктора II. Тихоходный вал редуктора
|
|
|
III. Вал привода рабочей машины
 1. Выбор двигателя. Кинематический расчёт привода.
1. Выбор двигателя. Кинематический расчёт привода.
1. 1. Требуемая мощность на ведущем валу редуктора, Р (кВт).
Рдв. р. = Р3 общ.

|
1. 2. Коэффициент полезного действия привода [7, с. 25, табл. №1]
hобщ. =hпк × hзп × hпк × hм × hоп =
= 0, 99 × 0, 96 × 0, 99 × 0, 98× 0, 97 = 0, 894
где
hоп = 0, 97 - кпд открытой передачи (ременной) hзп = 0, 96 – кпд закрытой передачи (редуктора) η м = 0, 98 - кпд муфты
η пк = 0, 99 - кпд пары подшипников качения
1. 3. Выбор электродвигателя [7, с. 25, табл. №2]
Электродвигатель выбирают из условия Рдв ³ Рдв. р. , применив для расчёта 4 варианта типа двигателя.
| Тип двигателя | Рдв. (кВт) | nдв(мин-1) |
| 4А90L2У3 4А100S4У3 4А112МA6У3 4А112MB8У3 | 3, 0 | 2905 1415 950 710 |
1. 4. Действительное общее передаточное число, для каждого варианта

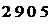 uo1 = 112 = 25, 938
uo1 = 112 = 25, 938
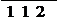 uo 2 = 1415 =12, 634
uo 2 = 1415 =12, 634
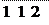 uo3 = 950 = 8, 482
uo3 = 950 = 8, 482
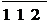 uo4 = 710 = 6, 339
uo4 = 710 = 6, 339
1. 5. Разбивка передаточного числа. [7, с. 26, табл. №3]
Выбираем передаточное число закрытой передачи uзп = 2, 0 - постоянным Передаточное число открытой передачи определяем по формулам:
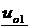
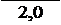
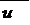
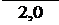 uоп1 = uзп = 25, 938 =12, 969 uоп2 = uo2 = 12, 634 = 6, 317
uоп1 = uзп = 25, 938 =12, 969 uоп2 = uo2 = 12, 634 = 6, 317
зп

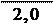 uоп3 = uзп = 8, 482 = 4, 241
uоп3 = uзп = 8, 482 = 4, 241
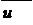
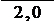 uоп4 = uo4 = 6, 339 = 3, 17 зп
uоп4 = uo4 = 6, 339 = 3, 17 зп
1. 6. Окончательно принимаем двигатель 4А112MB8Y3с параметрами:
Рдв = 3, 0кВт
nдв = 710об/ мин uзп = 2
uоп. = 3, 17
1. 7. Силовые и кинематические параметры привода. 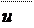

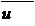
1. 7. 1. Мощность каждой ступени привода, кВт.
|
|
|
|
1. 7. 2. Частота вращения каждой ступени, об/мин.
|
|
| |
n2 = 1 зп
|
|
|
= 2, 0 = 355
n3 = n2 оп

| |
1. 7. 3. Угловая скорость каждой ступени, с-1
 wдв = pnдв = 3, 14× 710 = 74, 313с-1
wдв = pnдв = 3, 14× 710 = 74, 313с-1
| |
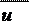
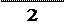
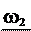 w2 = w1 = 74, 313 = 37, 157 зп
w2 = w1 = 74, 313 = 37, 157 зп
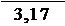 w3 = uоп = 37, 157 =11, 721
w3 = uоп = 37, 157 =11, 721
1. 7. 4. Вращающий момент Т, Нм
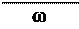
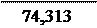 Тдв = Рдв. р × 103 = 2, 483× 1000 = 33, 413Нм
Тдв = Рдв. р × 103 = 2, 483× 1000 = 33, 413Нм
| |
Т2 =Т1 × uзп × hзп × hпк × hм =33, 079× 2× 0, 96× 0, 99× 0, 98= 61, 618Нм Т3 =Т2 × uоп × hоп = 61, 618× 3, 17× 0, 97 =189, 47Нм
1. 8. Сводная таблица силовых и кинематических параметров привода. 
2. Выбор материала зубчатой передачи.
| |
2. 1. Материал шестерни:
| |
|
|
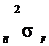 40Х s = 750МПа; s = 520МПа; НВ = 240;
40Х s = 750МПа; s = 520МПа; НВ = 240;
|
|
|
2. 3. 1. Допускаемые напряжения s Н для расчёта на контактную выносливость определяются по формуле:
|
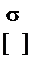 [ ]Н » 2, 75× НВ× kрк (Н / мм2 ), [ ]Нш » 2, 75× 270× 1= 742, 5(Н / мм2 )
[ ]Н » 2, 75× НВ× kрк (Н / мм2 ), [ ]Нш » 2, 75× 270× 1= 742, 5(Н / мм2 )
s Нк » 2, 75× 240× 1= 660(Н / мм2 )
где: НВ- твёрдость материала зубчатого колеса по Бринеллю;

 kрк - коэффициент режима нагрузки при расчёте на контактную прочность.
kрк - коэффициент режима нагрузки при расчёте на контактную прочность.
k ркш = 6
NБ 107
|
= 0, 448 Принимаем Кркш=1;
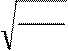 k ркк = 6
k ркк = 6
NБ NЦк
 = 6
= 6
61, 344× 107
= 0, 503 Принимаем Кркк=1;
Число циклов нагружения NЦ каждого зуба рассчитываемого колеса за весь срок службы передачи определяются по формуле:
|
|
где n - частота вращения зубчатого колеса, мин-1 ;
Lh = tГ × tД × tч - расчетная долговечность редуктора, час; Lh = 6∙ 300∙ 16=2880
tГ срок службы редуктора в годах; (6 лет) tД число рабочих дней в году; (300 дней)
tч число часов работы редуктора в течение рабочего дня; (16 часов) а число зацеплений зуба за один оборот колеса, обычно, а =1;
Базовое число циклов нагружения для сталей NБ =107 циклов.
2. 3. 2. Допускаемое напряжение от изгиба при расчёте зубьев по пределу выносливости:
|
|
|
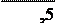
|
|

|
|
где - [n]=1, 5- требуемый (допускаемый) коэффициент запаса прочности [7, с. 26, табл. №6]
Кs =1, 5- эффективный коэффициент концентрации напряжений у основания
зуба [7, с. 27, табл. №7]
s-1 предел выносливости материала при симметрическом цикле нагружения может быть вычислен:
для легированных сталей s-1 = 0, 35× sв + (70... 120), Н / мм2
s-1ш = 0, 35× 950+ 70 = 402, 5, 5Н / мм2 s-1к = 0, 35× 750+70 =332, 5Н / мм2
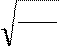 Крu - коэффициент режима нагрузки при расчёте зубьев на изгиб.
Крu - коэффициент режима нагрузки при расчёте зубьев на изгиб.

|
|
рuш 122, 688× 107
k рu = 9
= 0, 586
NБ NЦ
Принимаем Кркш=1;
 kрuк = 9
kрuк = 9
61, 344× 107
= 0, 633 Принимаем Кркк=1;
Число циклов нагружения Nц определяют по формуле:
|
|
2. 4. Сводная таблица данных: 
Механические характеристики материалов зубчатой передачи.
3. Расчет закрытой цилиндрической зубчатой передачи.
Проектный расчёт.
3. 1. Главный параметр – межосевое расстояние аW , мм:
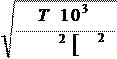 аW ³ Ка × (u+1)3 yа× u× × s]H × KHb где, Ка = 43- вспомогательный коэффициент.
аW ³ Ка × (u+1)3 yа× u× × s]H × KHb где, Ка = 43- вспомогательный коэффициент.
yа = 0, 25- коэффициент ширины шестерни относительно межосевого расстояния [7, с. 27, табл. №8]
u = 2 – передаточное число редуктора
|
|
s Н = 660 МПа - допускаемое контактное напряжение колеса с менее прочным зубом
KHb = 1 - коэффициент неравномерности нагрузки по длине зуба.
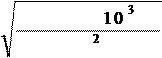
|
3. 2. Модуль зацепления m, мм;
 2× K × T × 103 2× 5, 8× 61, 618× 1000 d2 × b2 × [ ]F 94, 7× 17× 147, 777
2× K × T × 103 2× 5, 8× 61, 618× 1000 d2 × b2 × [ ]F 94, 7× 17× 147, 777
Принимаю m = 3мм; [7, с. 27, табл. №10]
|
|
|
где, Кm = 5, 8 - вспомогательный коэффициент.
d2 = 2аW × u/(u +1)- делительный диаметр колеса, мм; d2 =2∙ 71∙ 2∕ 3=94, 7мм
b2 =ya × aW - ширина венца колеса, мм;
b2 =0, 25∙ 71=17, 75 Принимаю b2=17мм [7, с. 27, табл. №11]
|
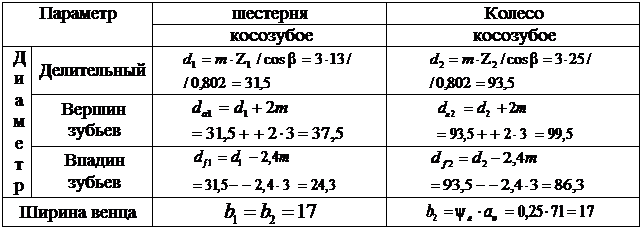
3. 3. Угол наклона зубьев bmin для косозубых передач: bmin = arcsin 3, 5m/b2 =38, 14451
3. 4. Суммарное число зубьев шестерни и колеса: для косозубых колёс:
ZS = Z1 + Z2 = 2× aw × соsbmin /m = 2× 71× cos38, 14451/3 = 37, 204 Принимаю ZS =38
3. 5. Действительная величина угла наклона зубьев для косозубых передач: b = arccos× ZS × m/2aw = arccos× 38× 3/2× 71= 36, 60005
3. 6. Число зубьев шестерни: Z1 = ZS /(1+u) =12, 66 Принимаю Z1 =13
3. 7. Число зубьев колеса: Z2 = ZS -Z1 =38-13= 25
3. 8. Фактическое передаточное число uф , проверить его отклонение uот заданного u:
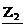
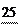 uф = Z1 = 13 =1, 923
uф = Z1 = 13 =1, 923




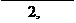

|
|
3. 9. Фактическое межосевое расстояние: для косозубых передач aw = (Z1 + Z2 )× m/(2cosb) = (13+ 25)× 3/(2× 0, 802) = 71
3. 10. Основные геометрические параметры передачи, мм.
Проверочный расчёт
3. 11. Расчёт зубьев на контактную прочность.
Проверка зубьев на контактную прочность: расчётное контактное напряжение
|
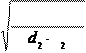
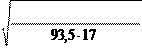
|
|
|
|
КHa = 1, 16 - коэффициент, учитывающий распределение нагрузки между зубьями [7, с. 28, табл. №13]
v = w2 × d2 /(2× 103), м/с,
v =37, 157× 93, 5/2000 =1, 737, м/с
и степени точности передачи =9 [7, с. 27, табл. №12]
КHv =1, 05- коэффициент динамической нагрузки, зависящий от окружной скорости колёс и степени точности передачи [7, с. 28, табл. №14]
3. 12. Расчёт зубьев на выносливость при изгибе. Для косозубых передач
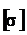
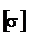
|
|
|
|
|
|


|
s F =147, 777 - расчётное и допускаемое напряжение от изгиба зуба, МПа; Т2 =61, 618 - расчётный момент на валу колеса, Нм;
| |
YF =3, 7– коэффициент формы зуба колеса [7, с. 28, табл. №15]
3. 13. Основные геометрические параметры зубчатой цилиндрической передачи (сводная таблица).
|
|
|
Проектный расчёт
| Шестерня | Колесо |
| Элементы зубьев (мм) | |
| Высота головки зуба ha = m=3 | |
| Высота ножки зуба hf =1, 25m=3, 75 | |
| Полная высота зуба h=2, 25m=6, 75 | |
| Диаметр делительных окружностей | |
| d1 =31, 5 | d2 =93, 5 |
| Диаметры окружностей выступов | |
| da1 =37, 5 | da2 =99, 5 |
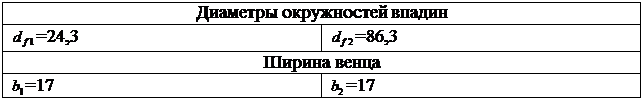
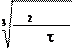
|
|
Проверочный расчёт
| Параметр | Расчётные значения | Допускаемые значения |
| Контактные напряжения sН , МПа | 654, 334 | |
| Напряжения изгиба, sF , МПа | 4, 961 | 147, 777 |
4. Проектный расчёт валов.
4. 1. Выбор материала валов.
применяю термически обработанную сталь 45 [7, с. 26, табл. №4] 4. 2. Выбор допускаемых напряжений на кручение.
|
|
|
|
|
|
|
4. 3. Определение геометрических параметров ступеней валов.
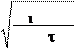 4. 3. 1. Диаметр вала под элемент открытой передачи:
4. 3. 1. Диаметр вала под элемент открытой передачи:
Т × 103
|
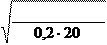 = 3 33, 079× 1000 = 20, 159Принимаю d1ш=20мм; [7, с. 29, табл. №18]
= 3 33, 079× 1000 = 20, 159Принимаю d1ш=20мм; [7, с. 29, табл. №18]
Т × 103 1К 0, 2× [ ]
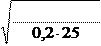 = 3 61, 618× 1000 = 23, 026мм Принимаю d1к=23мм; [7, с. 29, табл. №18]
= 3 61, 618× 1000 = 23, 026мм Принимаю d1к=23мм; [7, с. 29, табл. №18]
где, Т1 =33, 079Т2 =61, 618- крутящие моменты равные вращающим моментам на валах, Нм;
Длина вала под элемент открытой передачи:
| |
| |
l1 = (1, 0-1, 5)× d1 - под полумуфту;
| |
|
4. 3. 2. Диаметр вала под подшипник и уплотнение крышки с отверстием: d2 = d1 +2× t, где t значение высоты буртика [7, с. 28, табл. №16]
d2ш = 20+ 2× 2 = 24мм Принимаю d2ш=25мм; [7, с. 29, табл. №17] d2к = 23+2× 2 = 27ммПринимаю d2к=30мм; [7, с. 29, табл. №17]
Длина вала:
l2 =1, 5× d2 - вал- шестерня цилиндрическая l2ш =1, 5× 25 = 38мм [7, с. 27, табл. №11] l2 =1, 25× d2 - вал колеса
l2к =1, 25× 30 = 37, 5мм Принимаю l2k = 38мм [7, с. 27, табл. №11]
4. 3. 3. Диаметр вала под шестерню, колесо:
d3 = d2 +3, 2× r; [7, с. 28, табл. №16]
d3ш = 25+3, 2× 1, 6 = 29, 6мм Принимаю d3ш= 30мм; [7, с. 29, табл. №18] d3к = 30+3, 2× 1, 6 = 36, 12ммПринимаю d3к =36мм; [7, с. 29, табл. №18]
4. 3. 4. Решение вопроса о конструкции вала- шестерни [7, с. 29, табл. №19]
Расстояние Х от впадины зуба до шпоночного паза:
 Х = df 1 - d3ш -tв = 24, 3-30 - 4, 2 = -7, 05
Х = df 1 - d3ш -tв = 24, 3-30 - 4, 2 = -7, 05
Вал-шестерня
5. Конструктивные размеры зубчатой пары. Составление расчетной схемы нагружения валов.
5. 1. Шестерни конструируют в двух исполнениях: отдельно от вала (насадная шестерня) и как одно целое с валом (вал-шестерня).
Зубчатые колёса состоят из обода, несущего зубья; ступицы, насаживаемой на вал, и диска, соединяющего обод со ступицей.
5. 1. 1. Определение размеров зубчатых металлических колёс
| Параметр | Колесо |
| Диаметр ступицы стальных колёс | dст »1, 6× dв =1, 6× 36 = 57, 6 |
| Длина ступицы | lст =1, 5× dв =1, 5× 36 = 54 |
| Толщина обода цилиндрических колёс | dо = (2, 5... 4)× m = 3× 3= 9 dо ³ 8мм |
| Толщина диска штампованных колёс | С=0, 2× b=0, 2∙ 17=3, 4 |
| Внутренний диаметр обода | Do = da - 2× (dо + h) = 99, 5- 2× (9+ 6, 75) = 68, 2 где, h = 2, 25× m = 2, 25× 3 = 6, 75 |
| Выясняем надо ли, делать облегчающие отверстия в зубчатых колёсах; для этого проверяем, соблюдается ли условие | df /dв £ 2, 5 84, 3/36 = 2, 35³ 2, 5 |
| Толщина ребер | S=0, 8× C=0, 8∙ 3, 4=2, 72 |
| Фаска | n=0, 5m=0, 5× 3=1, 5 |
5. 2. В корпусе редуктора размещаются детали зубчатых передач. При его конструировании должны быть обеспечены прочность и жёсткость, исключающие перекосы валов.
Для повышения жёсткости служат рёбра, располагаемые у приливов, под подшипники. Корпус выполняют разъемным, состоящим из основания (его иногда называют картером) и крышки. Полость разъема проходит через оси валов.
Материал корпуса чугун СЧ10
5. 2. 1. Основные элементы корпуса из чугуна
| Параметры | Ориентировочные соотношения (размеры, мм) |
| Толщина стенки корпуса и крышки редуктора одноступенчатого цилиндрического | d =(0, 025× aw +1) =3, 5мм Принимаюdmin = 8, 0мм d1 = (0, 025× aw +1) = 3, 5мм Принимаюdmin = 8, 0мм |
| Толщина верхнего пояса (фланца) корпуса | b=1, 5∙ δ =12 |
| Толщина нижнего пояса (фланца) крышки корпуса | b1=1, 5∙ δ 1=12мм |
| Толщина нижнего пояса корпуса: без бобышки при наличии бобышки | p=2, 35∙ δ =18, 8 p1=1, 5∙ δ 1 =12 p2=2, 75∙ δ =18 |
| Толщина рёбер основания корпуса | m= (0, 85 – 1) ∙ δ =8мм |
| Толщина рёбер крышки | m1= (0, 85 – 1) ∙ δ 1=8мм |
| Диаметр фундаментных болтов (их число z > 4) | d1 = 0, 036 ∙ aw +12=16мм Принимаю М16 |
| Диаметр болтов у подшипников, соединяющих основание корпуса с крышкой | d2= 0, 75∙ d1 =12 Принимаю М12 d3 =0, 5∙ d1 =8 Принимаю М10 |
| Винты (болты) крепления крышки подшипника d4 Число винтов (болтов) n | принимаю М 8 принимаю n = 4 |
| Наименьший зазор между наружной поверхностью колеса и стенкой корпуса по диаметру по торцам | A= (1 – 1, 2) ∙ δ =8 A1=A |
5. 3. Предварительно выбираем подшипники [7, с. 30, табл. №21] 5. 3. Данные подшипников. 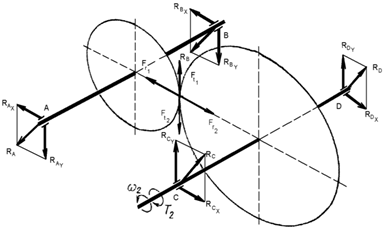
|
Вал | Размер в мм. | Условное обозначен ие подшипни ка | Грузоподъёмность, кН | |||
| Диаметр в месте посадки подшипника | Подшипник | Динамичес кая С | - Статическ ая Со | |||
| Ширина В, мм | Диаметр наружного кольца D, мм | |||||
| Ведущий | 11, 2 | 5, 6 | ||||
| Ведомый | 13, 3 | 6, 8 | ||||
5. 4. Определение расстояния между точками приложения реакций опор подшипников L (мм)
L = lст + 2А+ В=67мм Принимаю L =84мм lст- длина ступицы колеса
А – зазор между боковой поверхностью ступицы колеса и стенкой корпуса редуктора
В – ширина подшипника ведомого вала
5. 5. Предварительная компоновка горизонтального редуктора
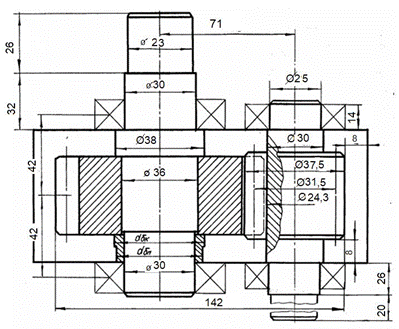 5. 6. Изображаем схемы вала шестерни и вала колеса редуктора с указанием сил, возникающих в зацеплении.
5. 6. Изображаем схемы вала шестерни и вала колеса редуктора с указанием сил, возникающих в зацеплении.
Схема нагружения валов цилиндрического одноступенчатого редуктора.
5. 6. 1. Окружное усилие Ft, возникающее в зубчатой передаче:
|
|
|
|
|
где d2 = 93, 5мм - диаметр делительной окружности колеса,
|
для косозубых передач:
|
|
b - угол наклона зубьев в косозубых передачах;
|
6. Проверка долговечности подшипников.
Подбор подшипников производится по расчётам отдельно для быстроходного и тихоходного валов.
Шестерня
6. 1. 1. Вычерчиваем расчётную схему вала в соответствии с выполненной схемой нагружения валов.
|
6. 1. 3. Определяем реакции в опорах подшипников в горизонтальной плоскости RAX ; RBX .
ì -F1 × L/2-RBx × L =0 î RAx × L+F1 × L/2=0
|
6. 1. 4. Строим эпюру изгибающего момента в горизонтальной плоскости МГ . M1 = -RAx × 0 = 0Нм
|
M3 = -RBx × L/ 2 =11. 627Нм
6. 1. 5. Определяем реакции в опорах подшипников в вертикальной плоскости
RAY ; RBY .
|
|
 ï RBy = 587, 893H î RAy = 587, 893Н
ï RBy = 587, 893H î RAy = 587, 893Н
6. 1. 6. Строим эпюру изгибающего момента в вертикальной плоскости MB .
M1 = -RAy × 0 = 0Нм
M2 = -RAy × L/2 = -24, 692Нм M4 = -RBy × 0 = 0Нм
M3 = -RBy × L/2 = -24, 692Нм

 6. 1. 7. Определяем суммарные реакции опор RА = RАХ 2 + RАY 2 , RB = RBХ 2 + RBY 2 ,
6. 1. 7. Определяем суммарные реакции опор RА = RАХ 2 + RАY 2 , RB = RBХ 2 + RBY 2 ,

 RA = (-276, 824)2 +587, 8932 = 649, 807Н RВ = (-276, 824)2 +587, 8932 = 649, 807Н
RA = (-276, 824)2 +587, 8932 = 649, 807Н RВ = (-276, 824)2 +587, 8932 = 649, 807Н



 6. 1. 8. Определяем суммарный изгибающий момент Мu = MГ 2 + MB2 . Мu1 = Mr12 + MB12 =0
6. 1. 8. Определяем суммарный изгибающий момент Мu = MГ 2 + MB2 . Мu1 = Mr12 + MB12 =0
Мu2 = Mr2 + MB2 =
 Мu3 = Mr 2 + MB2 =
Мu3 = Mr 2 + MB2 =
(11, 627)2 +(-24, 692)2 = 27, 293Hм
 (11, 627)2 +(-24, 692)2 = 27, 293Hм
(11, 627)2 +(-24, 692)2 = 27, 293Hм
Мu4 = 0.
| |


 6. 1. 10. Определяем эквивалентный момент и стоим эпюру Мn = Мu2 + МК 2 Мn1 = 0
6. 1. 10. Определяем эквивалентный момент и стоим эпюру Мn = Мu2 + МК 2 Мn1 = 0
Мn 2 = Мu22 +МК 2 =
 Мn3 = Мu22 +МК 2 =
Мn3 = Мu22 +МК 2 =
27, 2932 +33, 0792 = 40, 195Нм
 27, 2932 +33, 0792 = 40, 195Нм
27, 2932 +33, 0792 = 40, 195Нм
Мn 4 = 0
Колесо
6. 2. 1. Вычерчиваем расчётную схему вала в соответствии с выполненной схемой нагружения валов.
|
6. 2. 3. Определяем реакции в опорах подшипников в горизонтальной плоскости
RСX ; RDX .
|
|
|
|
6. 2. 4. Строим эпюру изгибающего момента в горизонтальной плоскости МГ .
M1 = RCx × 0 = 0Нм
M2 = RCx × L/2 = -11, 627Нм M4 = RDx × 0 = 0Нм
M3 = RDx × L/2 = -11, 627Нм
6. 2. 5. Определяем реакции в опорах подшипников в вертикальной плоскости
RCY ; RDY .
|
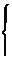 ï - t2 × L/2+ RDy × L = 0
ï - t2 × L/2+ RDy × L = 0
|
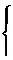 ï RDy = 587, 893H î RCy = 587, 893Н
ï RDy = 587, 893H î RCy = 587, 893Н
6. 2. 6. Строим эпюру изгибающего момента в вертикальной плоскости MB . M1 = RCy × 0 = 0Нм
M2 = RCy × L/2 = 24, 692Нм M4 = RDy × 0 = 0Нм
M3 = RDy × L/2 = 24, 692Нм

 6. 2. 7. Определяем суммарные реакции опор RC = RCХ 2 + RCY 2 , RD = RDХ 2 + RDY 2 ,
6. 2. 7. Определяем суммарные реакции опор RC = RCХ 2 + RCY 2 , RD = RDХ 2 + RDY 2 ,

 RС = (-276, 824)2 +587, 8932 = 649, 807Н RD = (-276, 824)2 +587, 8932 = 649, 807Н
RС = (-276, 824)2 +587, 8932 = 649, 807Н RD = (-276, 824)2 +587, 8932 = 649, 807Н


 6. 2. 8. Определяем суммарный изгибающий момент Мu1 = Mr12 + MB12 =0
6. 2. 8. Определяем суммарный изгибающий момент Мu1 = Mr12 + MB12 =0
Мu2 = Mr 2 + MB2 =
 Мu3 = Mr2 + MB2 =
Мu3 = Mr2 + MB2 =
(-11, 627)2 +(24, 692)2 = 27, 293Hм
 (-11, 627)2 +(24, 692)2 = 27, 293Hм
(-11, 627)2 +(24, 692)2 = 27, 293Hм
Мu4 = 0.
6. 2. 9. Определяем крутящий момент на валу и строим эпюру
MK =Т2 =61, 618Нм;
6. 2. 10. Определяем эквивалентный момент и стоим эпюру

 Мn1 = 0
Мn1 = 0
Мn 2 = Мu22 +МК 2 =
 Мn3 = Мu22 +МК 2 =
Мn3 = Мu22 +МК 2 =
27, 2932 +61, 6182 = 66, 371Нм
 27, 2932 +61, 6182 = 66, 371Нм
27, 2932 +61, 6182 = 66, 371Нм
Мn 4 = 0
6. 3. Окончательный выбор подшипников.
Для подбора типоразмера подшипника требуемый коэффициент работоспособности подшипника, определяем по формуле:
СТР = 0, 2× Q(w× h)0, 3 ,
СТРш = 0, 2× Q(w× h)0, 3 = 0, 2× 830, 472× (74, 313× 5000)0. 3 = 7, 787кН СТР = 0, 2× Q(w × h)0, 3 = 0, 2× 830, 472× (37, 157× 5000)0. 3 = 6, 325кН
где Q – расчётная нагрузка, воспринимаемая подши
|
|
|


