 |
Кинематика точки (задача К1)
|
|
|
|
4.1 Условие задачи К1
По заданным уравнениям движения точки 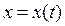 и
и  , заданным в таблице 6, найти и построить на рисунке в масштабе:
, заданным в таблице 6, найти и построить на рисунке в масштабе:
– траекторию движения точки;
– положение точки Мо в начальный момент времени  = 0;
= 0;
– положение точки М1 в заданный момент времени  , с;
, с;
– скорость и ускорение точек Мо и М1 в начальный и заданный моменты времени;
– касательное и нормальное ускорения, радиус кривизны траектории для точек Мо и М1.
4.2 Пример решения задачи К1
Движение точки задано координатным способом уравнениями:
x = 2 sin ( t) + 3; y = 4 cos (
t) + 3; y = 4 cos ( t). (4.1)
t). (4.1)
Для момента времени t = 1c определить кинематические параметры ее движения в соответствии с условием задачи К1.
Решение
Уравнения движения являются одновременно уравнениями траектории точки в параметрической форме. Для получения уравнения траектории из уравнений движения необходимо исключить параметр t:
sin ( t) =
t) =  ; cos (
; cos ( t) =
t) = 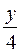 .
.
Если обе части каждого равенства возвести в квадрат и сложить левые и правые части, то получим уравнение эллипса:
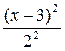 +
+  = 1. (4.2)
= 1. (4.2)
Полуоси эллипса: горизонтальная  = 2 м, вертикальная b = 4 м, координаты его центра
= 2 м, вертикальная b = 4 м, координаты его центра  = 3 м;
= 3 м;  = 0.
= 0.
Траекторию точки строим в масштабе на рисунке (рис. 73).
Для определения положения точки на траектории в уравнения ее координат подставляем соответствующее время.
В начальный момент времени при t = 0 из уравнений (4.1) получим:
 = 3 м,
= 3 м, 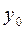 = 4 м.
= 4 м.
В заданный момент времени при  = 1 c из этих уравнений найдем:
= 1 c из этих уравнений найдем:
 = 2 sin
= 2 sin  + 3 = 4,4 м;
+ 3 = 4,4 м;  = 4 cos
= 4 cos  = 2,8 м.
= 2,8 м.
Положения точек Мо и М1 показываем на траектории (рис. 73).
Скорость и ускорение точки найдем по их проекциям на оси координат:  ;
;  ; (4.3)
; (4.3)
 ;
;  . (4.4)
. (4.4)
Тогда в начальный момент времени при t = 0 получим:
 м/с;
м/с;  ;
;
 = 1,57 м/с;
= 1,57 м/с;
 ;
; 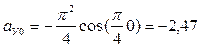 м/
м/  ;
;
 .
.
В заданный момент времени при  :
:
|
|
|
 ;
;  ;
;
 ;
;
 ;
;  ;
;
 .
.
Выбираем масштаб скорости и ускорения и строим векторы скорости и ускорения и их проекции для точек Мо и М1 (рис. 73). Величину выбранного масштаба необходимо указать на рисунке.
Определим касательное, нормальное ускорения точки и радиус кривизны ее траектории.
При движении точки по криволинейной траектории ускорение точки можно выразить через проекции на естественные оси: касательную и нормаль:  ,
,
где  – касательное ускорение точки:
– касательное ускорение точки:  ; (4.5)
; (4.5)
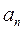 – нормальное ускорение:
– нормальное ускорение:  ; (4.6)
; (4.6)
 – радиус кривизны траектории.
– радиус кривизны траектории.
Нормальное ускорение можно вычислить, зная полное ускорение точки и его касательную составляющую:  . (4.7)
. (4.7)
Подставляем в формулы (4.50), (4.51), (4.52) значения величин, найденных для соответствующих моментов времени. В начальный момент времени при  :
:
 ;
;  ;
; 
В заданный момент времени при  :
:

 ;
; 
 |
Рисунок 73 – Схема к решению задачи К1
Таблица 1 – Исходные данные к задаче К1
| Номер варианта | Уравнения движения точки, м | Заданный момент времени, с | |
x = 
| y = 
| ||
х = 4cos 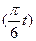 +3 +3
| у = 5sin 
| ||
х = 3sin 
| у = 4cos 
| ||
х = 6sin 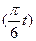
| у = 2cos(
| ||
х = 4cos (
| у = 2sin 
| ||
х = 4cos 
| у = 3sin(
| ||
х = 4sin(
| у = 2cos  t) t)
|
Продолжение таблицы 1
х = 5-2cos 
| у = 3sin(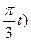 -1 -1
| ||||
х = sin(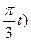
| у = 2cos  -3 -3
| ||||
х = 3cos 
| у = 2sin 
| ||||
х = 2sin 
| у = 4cos(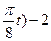
| ||||
х = 4sin(
| у = 5cos 
| ||||
х = 5sin(
| у = 2cos(
| ||||
х = 3sin(
| у = 6cos 
| ||||
х = 3cos(
| у = 2 – 4sin 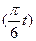
| ||||
х = sin(
| у = 2cos 
| ||||
х = sin 
| у = 4cos( )+2 )+2
| ||||
х = 2cos(
| у = 5sin(
| ||||
х = 5cos(
| у = 3sin 
| ||||
х = 2sin 
| у = 4cos 
| ||||
х = 4cos 
| у = 6sin 
| ||||
х = 2cos 
| у = 5sin 
| ||||
х = 6sin(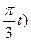
| у = 4cos 
| ||||
х = 5cos(
| у = 7sin 
| ||||
х = 3sin(
| у = 5cos 
| ||||
х = 4+2sin 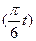
| у = 5cos 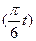
| ||||
х = 7sin 
| у = 4cos 
| ||||
х = 3sin( )+3 )+3
| у = 2cos( ) – 1 ) – 1
| ||||
Продолжение таблицы 1
х = -2cos(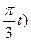
| у = 4sin 
| ||
х = 2sin  +3 +3
| у = 4cos  - 2 - 2
| ||
х = 2cos 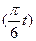 - 2 - 2
| у = 4sin 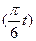 + 3 + 3
|
|
|
|
В выбранном масштабе ускорений показываем проекции ускорения точек Мо и М1 на естественные оси координат (рис. 73), что позволяет осуществить проверку решения.
На графике необходимо соблюсти условия:
 .
.
|
|
|


