|
Пример решения задачи первого типа
|
|
|
|
Исходные данные:
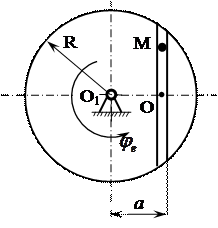
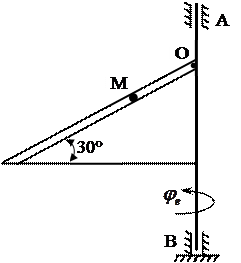
– ось вращательного движения пластины перпендикулярна плоскости чертежа и проходит через точку О1 (рис. 4, 5);
– закон вращательного движения пластины:  (рад);
(рад);
– закон движения точки по поверхности пластины:  (м);
(м);
– размер пластины: b = 40 см;
Определить абсолютную скорость и абсолютное ускорение точки М для момента времени t = t1= 1 с.
Решение
1. Квадратная пластина со стороной b (рис. 4) вращается в плоскости чертежа относительно оси, перпендикулярной этой плоскости и проходящей через точку О1. Подвижная система координат жестко связана с пластиной. Точка М совершает сложное движение:
· относительное – вдоль прямолинейного канала пластины;
· переносное – вместе с вращающейся пластиной.
2. Считаем, что положение пластины на рисунке соответствует углу поворота  в заданный момент времени t1 = 1 c.
в заданный момент времени t1 = 1 c.
3. Определим положение точки М на вращающейся пластине в заданный момент времени t1 = 1 с:
Sr = OM = 20 t2 =  = 20 см.
= 20 см.
Изобразим точку на пластине в заданном положении (рис. 4).
4. Найдем абсолютную скорость точки М по формуле
 . (8)
. (8)
Для определения модуля относительной скорости точки (Vr) продифференцируем по времени закон ее относительного движения:

При t1 = 1 c, Vr = 40  = 40 cм/с. Вектор
= 40 cм/с. Вектор  направлен в сторону, соответствующую положительному направлению относительной координаты S.
направлен в сторону, соответствующую положительному направлению относительной координаты S.

Рисунок 4 – Схема к определению абсолютной скорости точки
В переносном движении точка М в заданный момент времени движется вместе с вращающейся пластинкой по окружности радиуса О1М. Величину скорости точки при переносном вращательном движении найдем по формуле
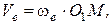
где  с-1.
с-1.
Положительное значение угловой скорости соответствует вращению пластины вокруг оси О1 в направлении, указанном на рисунке, то есть противоположном движению часовой стрелки. Расстояние точки М до оси вращения определим по формуле:
|
|
|


Вектор переносной скорости  направлен перпендикулярно радиусу О1М в сторону переносной угловой скорости
направлен перпендикулярно радиусу О1М в сторону переносной угловой скорости  (рис. 4).
(рис. 4).
Модуль абсолютной скорости найдем по ее проекциям на оси координат:
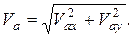 (9)
(9)
Оси координат х и у направим, как показано на рисунке 4.
Для вычисления проекций абсолютной скорости на оси координат найдем значения тригонометрических функций:

Тогда:

5. Абсолютное ускорение точки найдем по формуле:
 . (10)
. (10)
В относительном движении точка движется по прямолинейной траектории, поэтому относительное ускорение характеризует изменение относительной скорости только по величине и определяется по формуле:

Вектор относительного ускорения  (рис. 5) направлен так же, как и вектор относительной скорости, так как знаки
(рис. 5) направлен так же, как и вектор относительной скорости, так как знаки  и
и  совпадают, то есть точка М совершает относительное движение с ускорением.
совпадают, то есть точка М совершает относительное движение с ускорением.
В переносном движении точка движется по криволинейной траектории – окружности радиуса О1М, поэтому переносное ускорение будет представлено двумя составляющими:

 . (11)
. (11)
Рисунок 5 – К определению абсолютного ускорения точки
В векторном уравнении (11)  – нормальное ускорение, характеризует быстроту изменения переносной скорости точки по направлению, причем вектор
– нормальное ускорение, характеризует быстроту изменения переносной скорости точки по направлению, причем вектор  направлен к оси вращения О1:
направлен к оси вращения О1:

Касательное ускорение  – характеризует быстроту изменения переносной скорости по модулю, вектор
– характеризует быстроту изменения переносной скорости по модулю, вектор  направлен по касательной к траектории переносного движения точки:
направлен по касательной к траектории переносного движения точки:

где
 – угловое ускорение пластины в ее переносном вращательном движении.
– угловое ускорение пластины в ее переносном вращательном движении.
Численное значение  при t1 = 1 с определим из выражения:
при t1 = 1 с определим из выражения:

Так как знаки угловой скорости и углового ускорения совпадают, то переносное вращательное движение является ускоренным.
|
|
|
Таким образом 
Вектор  направлен перпендикулярно вектору
направлен перпендикулярно вектору  в сторону, соответствующую направлению углового ускорения
в сторону, соответствующую направлению углового ускорения  переносного вращательного движения пластины (рис. 5).
переносного вращательного движения пластины (рис. 5).
Модуль ускорения Кориолиса определяют по формуле:
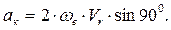
Вектор угловой скорости  перпендикулярен плоскости чертежа, то есть
перпендикулярен плоскости чертежа, то есть  , тогда:
, тогда:

Так как ось вращения пластины перпендикулярна плоскости чертежа, то для определения направления вектора ускорения Кориолиса необходимо лишь повернуть вектор относительной скорости  на 900 в сторону, соответствующую направлению переносной угловой скорости
на 900 в сторону, соответствующую направлению переносной угловой скорости  (рис. 5).
(рис. 5).
С учетом (10) формула (11) для вычисления абсолютного ускорения точки примет вид:
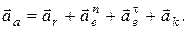 (12)
(12)
Для нахождения модуля абсолютного ускорения спроецируем векторное равенство (12) на координатные оси:


Тогда 
5.3 Пример решения задачи второго типа
Исходные данные:
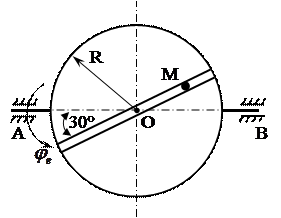
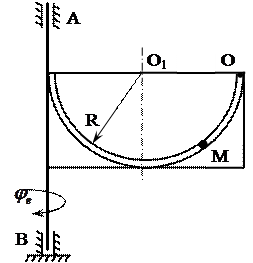
– ось АВ вращательного движения пластины (рис. 6) находится в плоскости чертежа;
– закон вращательного движения пластины  (рад);
(рад);
– закон движения точки М по поверхности пластины
 (м);
(м);
– радиус пластины R = 0,6 м.
 |
Определить абсолютную скорость и абсолютное ускорение точки М для момента времени t = t1= 1 с.
Рисунок 6 – Исходная схема к решению задачи
Решение
1. Пластина радиуса R (рис. 6) вращается вокруг неподвижной вертикальной оси АВ (оси z), совпадающей с плоскостью чертежа. Точка М совершает сложное движение, состоящее из относительного движения точки по ободу пластины и переносного движения вместе с пластиной, совершающей вращательное движение. При этом в переносном движении точка перемещается по окружности, расположенной в плоскости, перпендикулярной оси вращения z, причем центр окружности находится на этой оси. Считаем, что в момент времени t = t1=1 с, пластина заняла положение, показанное на рисунке 6.
2. Определим положение точки M на пластине в момент времени
t1 = 1 с:  м.
м.

Рисунок 7 – Схема к определению абсолютных
скорости и ускорения точки
Дуге ОМ соответствует центральный угол:

Точка О соответствует начальному положению точки М на пластине, тогда угол  отложим от горизонтального диаметра ОО1 в сторону, соответствующую положительному направлению отсчета относительной координаты S (рис. 6) поскольку значение Sr положительно.
отложим от горизонтального диаметра ОО1 в сторону, соответствующую положительному направлению отсчета относительной координаты S (рис. 6) поскольку значение Sr положительно.
|
|
|
3. Определим абсолютную скорость точки по теореме о сложении скоростей: 
Относительную скорость  определим из закона относительного движения:
определим из закона относительного движения:  м/c.
м/c.
Численное значение относительной скорости положительно и поэтому вектор  направляем по касательной к относительной траектории точки в сторону положительного отсчета относительной координаты S (рис.7).
направляем по касательной к относительной траектории точки в сторону положительного отсчета относительной координаты S (рис.7).
Так как переносное движение является вращательным, переносная скорость точки зависит от угловой скорости вращения пластины и расстояния h до оси вращения:

где  м;
м;
 с-1.
с-1.
Так как  >0, то пластина вращается в направлении, совпадающим с указанным на рисунке 7 углом ее поворота
>0, то пластина вращается в направлении, совпадающим с указанным на рисунке 7 углом ее поворота  . При этом вектор угловой скорости
. При этом вектор угловой скорости  совпадает с положительным направлением оси z. Тогда вектор переносной скорости
совпадает с положительным направлением оси z. Тогда вектор переносной скорости  будет направлен перпендикулярно отрезку МК в сторону вращения пластины, т.е. он направлен перпендикулярно плоскости чертежа (за чертеж, в противоположенную сторону от положительного направления оси x). Численное значение переносной скорости равно
будет направлен перпендикулярно отрезку МК в сторону вращения пластины, т.е. он направлен перпендикулярно плоскости чертежа (за чертеж, в противоположенную сторону от положительного направления оси x). Численное значение переносной скорости равно 
Векторы относительной скорости  и переносной скорости
и переносной скорости  взаимно перпендикулярны, поэтому абсолютную скорость точки определим по формуле:
взаимно перпендикулярны, поэтому абсолютную скорость точки определим по формуле:
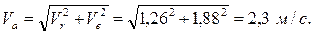
4. Абсолютное ускорение точки определим по теореме Кориолиса:
 (13)
(13)
Так как в относительном и переносном движениях точка движется по криволинейным траекториям, то относительная и переносная скорости будут изменяться по модулю и направлению, а векторы ускорений  и
и 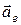 будут содержать касательную и нормальную составляющие. Тогда формула (13) примет вид
будут содержать касательную и нормальную составляющие. Тогда формула (13) примет вид
 (14)
(14)
Относительное нормальное ускорение 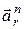 зависит от относительной скорости и радиуса кривизны траектории относительного движения точки, то есть радиуса R пластины:
зависит от относительной скорости и радиуса кривизны траектории относительного движения точки, то есть радиуса R пластины:
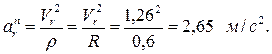
Вектор 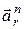 направлен к точке О1 – центру кривизны траектории точки М в ее относительном движении.
направлен к точке О1 – центру кривизны траектории точки М в ее относительном движении.
Относительное касательное ускорение  характеризует изменение модуля относительной скорости с течением времени
характеризует изменение модуля относительной скорости с течением времени

Вектор  направлен перпендикулярно вектору
направлен перпендикулярно вектору 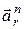 в сторону
в сторону  , так как знаки относительной скорости точки и ее относительного касательного ускорения совпадают.
, так как знаки относительной скорости точки и ее относительного касательного ускорения совпадают.
|
|
|
Переносное нормальное ускорение  зависит от угловой скорости вращающегося тела и расстояния до оси вращения:
зависит от угловой скорости вращающегося тела и расстояния до оси вращения:
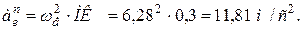
Вектор  направлен вдоль отрезка МК к оси вращения пластины, т.е. к центру траектории точки в ее переносном движении. Переносное касательное ускорение точки зависят от углового ускорения пластины
направлен вдоль отрезка МК к оси вращения пластины, т.е. к центру траектории точки в ее переносном движении. Переносное касательное ускорение точки зависят от углового ускорения пластины  и расстояния от точки М до оси вращения пластины:
и расстояния от точки М до оси вращения пластины:

где 
Знак углового ускорения  совпадает со знаком угловой скорости, следовательно, переносное вращательное движение является ускоренным
совпадает со знаком угловой скорости, следовательно, переносное вращательное движение является ускоренным
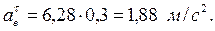
Вектор  направлен перпендикулярно вектору
направлен перпендикулярно вектору  и совпадает с направлением вектора переносной скорости
и совпадает с направлением вектора переносной скорости  , так как знаки их численных значений одинаковы.
, так как знаки их численных значений одинаковы.
Модуль ускорения Кориолиса определим по формуле (6) с учетом того, что угол между векторами  и
и  составляет 600:
составляет 600:
 м/с. (15)
м/с. (15)
Для определения направления вектора ускорения Кориолиса воспользуемся правилом Жуковского, в соответствии с которым вектор  будет направлен перпендикулярно плоскости чертежа в сторону, соответствующую положительному направлению оси х.
будет направлен перпендикулярно плоскости чертежа в сторону, соответствующую положительному направлению оси х.
Модуль абсолютного ускорения точки найдем, проецируя векторное равенство (4.39) на координатные оси:
 (16)
(16)
где 


Тогда численное значение абсолютного ускорения точки будет равно:

Таблица 2 – Исходные данные к задаче
| Номер варианта | Уравнение движения тела
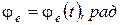
| Уравнение относительного движения точки М

| t1, с | R, см | а, см | |||

| 
| 0,5 | ||||||
| 2t2 + t | 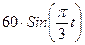
| 0,5 | ||||||
| 5t2 | 
| |||||||
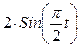
| 180 t2 | 1/3 | ||||||
| t + t2 | 
| |||||||
| 10t2 – 1 | 
| 1/3 | ||||||

| 
| |||||||
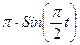
| 
| |||||||
| 3t2 | 
| 1/3 | ||||||
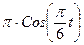
| 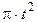
| |||||||

| 
| |||||||

| 
| |||||||
| Продолжение таблицы | ||||||||
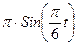
| 10 t3 | |||||||
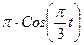
| 15 t2 | |||||||

| 
| 1/2 | ||||||
| 2t2 | 
| |||||||

| 40 t2 | |||||||
| 0,5t3 | 
| |||||||
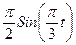
| 
| |||||||

| 45 t2 | 1/3 | ||||||
| 2 t+0,5 t2 | 
| 1/3 | ||||||
| 3 t2 – 1 | 
| |||||||
| 2 t2 - 1 | 
| |||||||
| 0,5t2+t2 | 
| |||||||

| 180 t2 | 1/3 | ||||||
| 4 t3 | 
| |||||||
| 0,5 t2 | 
| |||||||

| 
| |||||||

| 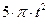
| |||||||

| 
| |||||||
|  2 2
| |||||||
  3 3
|
| |||||||
  5 5
|   6 6
| |||||||
Рисунок 8 - Расчетные схемы к задаче
|  8 8
| |||||
 9 9
|  10 10
| |||||
|  12 12
|
Рисунок 8, лист 2
 13 13
|   14 14
| |||
 15 15
|  16 16
| |||
|   18 18
|
Рисунок 8, лист 3
|   20 20
| |||
  21 21
|   22 22
| |||
|  24 24
|
Рисунок 8, лист 4
|  26 26
| |||||
|  28 28
| |||||
|  30 30
|
Рисунок 8, лист 5
5 Вопросы для самопроверки к разделу «Кинематика точки»
1. Что изучает кинематика?
2. Какое движение называется механическим. Приведите примеры?
3. Что называется системой отсчета? Зачем нужна система отсчета?
4. Сформулируйте основные задачи кинематики точки.
5. Перечислите способы задания движения точки.
6. Что называется траекторией точки? Приведите примеры.
7. Как задать движение точки векторным способом?
8. Как определить проекции радиуса-вектора на координатные оси?
9. Как задать движение точки координатным способом? Как определить уравнение траектории движения точки при этом способе задания движения?
10. Приведите примеры криволинейных траекторий движения точки, их уравнений.
11. При каких условиях можно задать движение точки естественным способом? Какие оси называются естественными? Как располагаются в пространстве естественные оси координат?
12. Какая взаимосвязь существует между естественным и координатным способами задания движения точки?
13. Что называется скоростью точки?
14. Как определить скорость точки при векторном способе задания движения?
15. Как определить модуль и направление вектора скорости при координатном способе задания движения?
16. Как определить модуль и направление вектора скорости при естественном способе задания движения точки?
17. Что называется ускорением точки?
18. Как определить ускорение точки при векторном способе задания движения?
19. Как определить модуль и направление вектора ускорения точки при координатном способе задания движения?
20. На какие оси естественной системы координат проецируется вектор ускорения? Как определить его модуль и направление?
21. Что характеризует нормальное ускорение точки?
22. Как определить модуль и направление нормального ускорения?
23. Что характеризует касательное ускорение точки?
24. Как определить модуль и направление касательного ускорения точки?
25. Как определить ускорение точки в частных случаях ее движения?
26. Как определить скорость и ускорение точки по заданному закону ее движения? В какой последовательности решается задача?
27. Какую систему координат целесообразно выбрать в случае криволинейной траектории движения точки?
28. Как определить закон движения точки в выбранной системе отсчета? В какой последовательности решается задача? Как определяются постоянные интегрирования?
29. Какое движение точки называется сложным?
30. Сформулируйте основные задачи сложного движения точки.
31. Какие движения точки называются относительным, переносным и абсолютным?
32. Какая скорость точки называется относительной?
33. Что является для точки переносной скоростью?
34. Сформулируйте теорему о сложении скоростей при сложном движении точки.
35. Какое ускорение точки называется относительным?
36. Какое ускорение для точки является переносным?
37. Сформулируйте теорем о сложении ускорений точки (теорему Кориолиса).
38. Как вычислить модуль ускорения Кориолиса и найти его направление?
39. В каких случаях поворотное или кориолисово ускорение равно нулю?
40. Перечислите основные пункты решения задач по разделу «Кинематика».
Список литературы
1. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т. 1 Статика. Кинематика. Т. 2 Динамика, - СПб. ЛАНЬ, 2002.-729 с.
2. Никитин Н.Н. Курс теоретической механики. -М.: ВШ,2003.-719 с.
3. Яблонский А.А., Никифорова В.М. Курс теоретической механики.- М.: ИНТЕГРА-ПРЕСС, 2007.-603 с.
4.Тарг С.М. Краткий курс теоретической механики.-М.:ВШ,2008.-416с.
5. Мещерский И.В. Сборник задач по теоретической механике. -М.: ЛАНЬ, 2003.-448 с.
6. Сборник задач по теоретической механике. / Под рук. К.С. Колесникова.- СПб.: ЛАНЬ, 2008.-448 с.
7. Сборник заданий для курсовых работ по теоретической механике / Под ред. А.А.Яблонского.- М.: ИНТЕГРА-ПРЕСС, 2008.-384 с.
8. Цывильский В.Л. Теоретическая механика. -М.:ВШ, 2001.- 319 с.
9. Митюшов Е.А., Берестова С.А. Теоретическая механика.- М.: Академия, 2006.-312 с.
Теоретическая механика
Часть 1
Статика, Кинематика
Составители: Смелягин Анатолий Игоревич
Кегелес Валерий Леонидович
Драйко Людмила Ивановна
Иосифова Лилиана Владимировна
Мельников Владимир Филиппович
Мхитарьянц Георгий Арамович
Редактор Т.Г. Горшкова
Компьютерная верстка В. Л. Кегелес, Л. И. Драйко
| Подписано в печать Бумага офсетная Печ. л. 2,75 Усл. печ. л. 2,5 Уч. – изд. л. 1,9 Цена | Формат 60 х 84 / 16 Офсетная печать Изд. № Тираж экз. Заказ № руб. |
Кубанский государственный технологический университет
350072, г. Краснодар, ул. Московская, 2, кор. А
Типография КубГТУ: 350058, г. Краснодар, ул. Старокубанская, 88/4
|
|
|