 |
Практическое применение метода ключевых задач в школьном курсе геометрии
|
|
|
|
Приведем системы, составленные методом «ключевых» задач, которые можно использовать для итогового повторения курса планиметрии.
Свойства медиан треугольника.
Ключевые задачи:
1. Медианы в треугольнике пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
2. Медиана делит треугольник на два равновеликих.
Пусть ВМ - медиана △АВС. Рассмотрим △АВМ, △МВС (Рисунок. 2.1).
Т.к. для △АВМ и △МВС ВН - высота общая, то
а, по условию, ВМ - медиана ⇒ АМ=МС ⇒ 
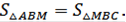
3. Медианы треугольника делят его на шесть равновеликих треугольников и SABC=3SAOB=3SBOC=3SCOA.
Доказательство.
Пусть ВК, СМ, АН - медианы △АВС, которые пересекаются в т.О (Рисунок. 2.2). Получим △АОВ, △ВОС, △АОС. Пусть их площади равны соответственно S1, S2, S3. А площадь △АВС равна S.
Рассмотрим △АВК и СВК - они равной площади, т. к. ВК - медиана.
В △АОС и ОК - медиана, значит 
Отсюда следует, что S2=S3, S3=S1, т.е. SABC=3SAOB=3SBOC=3SCOA
Обозначим площади △МОВ, △ВОН, △НОС, △СОК, КОА и △АОМ соответственно S1, S2, S3, S4, S5, S6.
Т.к. площади △АОВ, △ВОС, △АОС равны и площади △АОМ, △ВОМ равны, значит S1= S6. Аналогично S2= S3.
Если S1+ S6= S2+ S3 и 2S2=2S1, значит S2=S1. И так далее. Получим, что все шесть треугольника имеют равные площади и они составляют шестую часть от площади △АВС.
Задачи системы:
Задача 1. Две стороны треугольника соответственно равны 6 и 8. Медианы, проведенные к этим сторонам, перпендикулярны. Найдите площадь треугольника.
Решение.
Пусть AB=6, AC=8 (Рисунок. 2.3).
Тогда медианы СС1 и ВВ1перпендикулярны и пересекаются в точке О.
SABC=3SBOC.
SBOC= 
OB∙OC, так как треугольник ВОС прямоугольный.
|
|
|
По ключевой задаче: если ВВ1=x, то OB=2x; если OC1=y, то OC=2y. Треугольники ВОС1 и СОВ1 прямоугольные и по теореме Пифагора имеем
SBOC= 
.
Тогда SABC= 
Ответ: 
.
Задача 2. В треугольника АВС АА1 и СС1 - медианы, причем АА1=5, 
, 
. Найдите площадь треугольника АВС.
Тогда
, 
,
, 
.
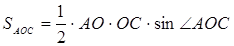Решение. 
ключевой задаче 
. 
. Длину стороны ОС найдем по теореме синусов (Рисунок. 2.4):
 ⇒  .
|
Ответ: 
.
Задача 3. Медианы треугольника 3, 4 и 5. Найдите площадь треугольника.
А1, В1, С1 - середины сторон ВС, АС и АВ соответственно (Рисунок. 2.5). Пусть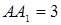 
, 
, 
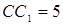. Тогда по ключевой задаче 
, 
, 
и 
. Достроим треугольник АОС до параллелограмма, отложив на прямой ВВ1 от точки В1 отрезок B1D, равный В1О.
Тогда  .
|
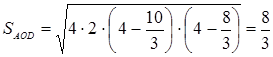. Следовательно, 
.
Ответ:
Задача 4. Длины двух сторон треугольника 27 и 29. Длина медианы, проведенной к третьей стороне, равна 26. Найдите высоту треугольника, проведенную к стороне длиной 27.
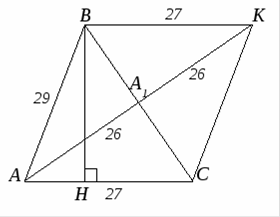
Пусть AB=29, AC=27, медиана AA1=26 (Рисунок. 2.6).
Чтобы найти высоту ВН достаточно знать площадь треугольника АВС. Чтобы найти площадь треугольника АВС достроим его до параллелограмма АВКС, продлив медиану АА1.
Тогда SABC=SABK= SABKC.
SABK= 
.
SABC= AC∙BH,
= ∙27∙BH,
BH=20.
Ответ: 20.
Длина медианы
Ключевая задача:
1. Докажите, что если стороны АВ, АС и ВС треугольника АВС равны соответственно с, b и а, то длина медианы, проведенной к стороне ВС, может быть вычислена по формуле
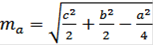
По теореме косинусов имеем:
Треугольник ABM (Рисунок. 2.7):
Треугольник АВС:
Сложим эти равенства, получим
Отсюда
2. Сумма квадратов медиан треугольника равна 
суммы квадратов его сторон.
Используя предыдущую ключевую задачу, получим:
3.
Сумма квадратов медиан прямоугольного треугольника, проведенных из вершин острых углов, равна 
квадрата его гипотенузы.
Пусть АМ, ВН - медианы △АВС (Рисунок. 2.8).
Из △АСМ: 
|
|
|
Из △RAH: 
Сложим равенство (1) и (2), получим
Задачи системы:
Задача 1. Найдите отношение суммы квадратов всех медиан треугольника к сумме квадратов всех его сторон.
Ответ: 
.
Задача 2.
. Найдем АС, используя формулу длины медианы (Рисунок. 2.9):
2. Треугольник АВС - прямоугольный, так как
Следовательно,
Ответ: 
.
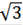Задача 3. Длины двух сторон треугольника равны 16 и 12. Медианы, проведенные к этим сторонам треугольника, перпендикулярны. Найдите третью сторону треугольника.
Проведем медианы АК и ВМ в треугольнике АОВ (Рисунок. 2.10). Заметим, что
Тогда, согласно третьей ключевой задаче, запишем:
Ответ: 
.
|
|
|
