Медиана, проведенная к гипотенузе .

Ключевая задача. В прямоугольном треугольнике длина медианы, проведенной к гипотенузе, равна ее половине.

 

Продлим отрезок CD и отметим на луче отрезок DM=CD, AMBC - четырехугольник (Рисунок. 2.11).

Докажем, что AMBC - прямоугольник. Рассмотрим △ADM и △CDB, по условию AD=AB, MD=DC; ∠ADM=∠CBD (как вертикальные), значит, △ADM=△CDB (по двум сторонам и углу между ними), следовательно, АМ=ВС.

Так же из △ADC=△BDM следует АС=МВ.

Значит, АМ=ВС, АС=МВ, ∠С=90^о, т.е.: АМВС - прямоугольник.

АВ и МС - диагонали прямоугольника АМСВ, т.е. АВ=МС, АD=DB=MD=DC, значит

Следствия:

1. Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.

. Если в треугольнике длина медианы равна половине длины стороны, к которой она проведена, то этот треугольник - прямоугольный.

Задачи системы:

Задача 1. Лестница скользит по стенкам угла. Какую траекторию описывает фонарик, находящийся на средней ступеньке лестницы?

 

 

По ключевой задаче  (Рисунок. 2.12). Аналогично, . Так как , то .

Множество точек, отстоящих от точки С на одинаковом расстоянии, лежат на окружности. Таким образом, фонарик, находящийся на средней ступеньке лестницы, описывает дугу окружности.

Задача 2. В трапеции углы при одном из оснований равны 30⁰ и 60⁰, длина отрезка, соединяющего середины оснований, равна 3. Найдите длины оснований трапеции и ее площадь, если длина средней линии равна 5.

 

 

Пусть ⌞BAD=60^o, ⌞CDA=30^o, тогда продолжения боковых сторон пересекаются под прямым углом (Рисунок. 2.13).

По ключевой задаче  и . Пусть , тогда .

По свойству средней линии трапеции: 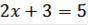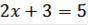, . Следовательно, .

 

 

Ответ:

Свойство биссектрисы.

Ключевая задача. Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные прилежащим сторонам.

 

 

Проведем CF, параллельно биссектрисе BD (Рисунок. 2.14). Тогда по теореме о пропорциональных отрезках . Треугольник BCF - равнобедренный.

Так как углы ∠ равны как соответственные при параллельных прямых BD и CF и секущей AF, углы ∠BCF и ∠CBD равны как накрест лежащие при параллельных прямых BD и CF и секущей ВС, ∠ABD=∠CBD по свойству биссектрисы. Следовательно, BF=BC. Тогда .

Задачи системы:

Задача 1. В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу на отрезки 3 и 4. Найдите площадь треугольника.

Пусть ,  (Рисунок. 2.16). Тогда по свойству биссектрисы , а по теореме Пифагора . Решая систему получим: , . Вычисляя площадь треугольника по формуле

 

,

 

получим .

О т в е т: 11,76.

Задача 2. В прямоугольном треугольнике проведена биссектриса острого угла. Отрезок, соединяющий ее с основание с точкой пересечения медиан, перпендикулярен катету. Найдите острые углы треугольника.

 

Пусть AD - биссектриса прямоугольного треугольника АВС). Точка О - точка пересечения медиан. Тогда по условию задачи .

По свойству медиан .

По теореме Фалеса .

 

Так как AD - биссектриса, то . Следовательно, .

Так как гипотенуза АВ в два раза больше катета АС, то 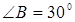. Следовательно, .

Ответ: 30⁰; 60⁰.

Задача 3. В равнобедренный треугольник АВС с основанием АС вписана окружность с центром О. Луч АО пересекает сторону ВС в точке К, причем 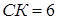, . Найдите периметр треугольника АВС.

 

Так как О - центр вписанной окружности, то АК - биссектриса треугольника АВС (Рисунок. 2.18). Тогда . Имеем , .

.

Ответ: 45.

Задача 4. Найдите стороны треугольника, если медиана и высота, проведенные из одного угла, делят его на три равные части, а длина медианы равна 10.

 

Р е ш е н и е. Пусть СN - медиана, а СК - высота (Рисунок. 2.19). Так как СК - высота и биссектриса, то треугольник CNB равнобедренный, следовательно,  и .

, следовательно, .

 

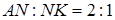CN - биссектриса в треугольнике АСК, следовательно,

Треугольник 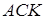 - прямоугольный, поэтому , , , , .

Ответ: .

Длина биссектрисы

Ключевая задача:

. Длину биссектрисы можно вычислить по формуле: l_a= , где l_a - длина биссектрисы, проведенной из угла A треугольника ABC, α = BAC, b, a - длины сторон треугольника.

 

 

Пусть площадь △АВС равна S, а площадь △АBD и △CAD равны соответственно S₁ и S₂ (Рисунок. 2.20)_.

Тогда S= S₁ + S_2,

 

 

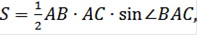
откуда,

 

Учитывая, что

 

 

получим

 

.

 

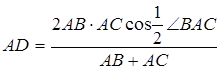2. Длину биссектрисы можно вычислить по формуле: , где  - длина биссектрисы, проведенной из угла A треугольника ABC, -

отрезки, на которые биссектриса делит сторону BC, b, a - длины сторон треугольника.

 

 

Применим теорему косинусов к △BAD и △CAD, получим

 

 

Умножим первое равенство на CD, а второе - на BD и сложим эти равенства

 

AB² ∙СD + AC² ∙BD = BD² ∙CD + CD² ∙DB + AD² ∙(BC+ DC) (1).

Так как биссектриса угла треугольника делит сторону, противоположную этому углу, на части, пропорциональные прилежащим сторонам, то

 

,

 

откуда

 

, .

 

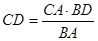Подставим эти выражения в левую часть равенства (1), получим

 

 

или

 

 

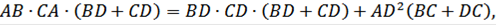
откуда

 

 

Заключение

обучение школьник геометрия биссектриса

Анализ использования метода ключевых задач в обучении показывает, что такой подход дает возможность ликвидировать не только перегрузку учащихся (решается меньшее число задач, меньше их задается на дом, заранее известно, какие типы задач подлежат опросу), но и существенно облегчает труд учителя по планированию уроков, проверке знаний учащихся.

В заключение отметим, что эффективность урока зависит от:

) знания учителем состава задач по теме и методов их решения;

) владения методами выделения ключевых задач и умелой их реализации;

) отсутствия формализма в требованиях по овладению умениями решать ключевые задачи;

) способности предвидеть затруднения, типичные ошибки учащихся и выбрать методы их предупреждения;

) умения правильно организовать контроль за умениями решать ключевые задачи и качественно провести анализ результатов контроля.

При использовании ключевых задач происходит наглядное моделирование мыслительного процесса. Таким образом, реализуется возможность перехода от «школы памяти» к «школе мышления». Пусть далеко не все ученики могут решить сложнейшую задачу, но понять предлагаемое решение и воспроизвести его этапы могут все. Учащиеся из пассивных слушателей превращаются в деятельных, активных участников образовательного процесса. Навыки и умения, полученные учащимися при выделении и решении непосредственно ключевых, а также комбинированных задач, создают прочную базу для дальнейшего изучения предмета на более углублённом уровне. Переход к нестандартным, творческим задачам становится более актуальным, т.к. на первый план выступает практическое применение полученных знаний.

Библиографический список

 

1) Готман, Э.Г. Задачи по планиметрии и методы их решения /

Э.Г. Готман. - М.: Мир, 1988. - 264 с.

) Методика преподавания математики в основной школе. Курс лекций [Электронный ресурс] / Александр Печко. - 2000-2012. - Режим доступа: http:// rudocs.exdat.com. - Дата доступа: 25.09.2013.

3) Колягин, Ю.М. Методика преподавания математики в средней школе / Ю.М. Колягин. - М.: Мир, 1980. - 375 с.

)   Зильберберг, Н.И. Ключевые задачи в обучении математике/

Н.И. Зильберберг, Р.Г. Хазанкин. - М: Мир, 1984. - 179 с.

) Электронная хрестоматия по методике преподавания математики. Методика обучения решению задач [Электронный ресурс] / Сазанова Т.А., Дубов А.Г. - 2000-2012. - Режим доступа: http://fmi.asf.ru/library/book/mpm/index.html. - Дата доступа: 10.10.2013.

6) Пирютко, О.Н. Геометрия в таблицах и задачах: планиметрия: для школьников / О.Н. Пирютко. - Минск: Аверсэв, 2008. - 122 с.

)   Тавгень, О.И. Математика в задачах. Теория и методы решений. Планиметрия, стереометрия, текстовые задачи / О.И. Тавгень,

А.И. Тавгень. - Минск: Аверсэв, 2005. - 511 с.

) Лисова, М.И. Планиметрия. Итоговое повторение / М.И. Лисова, О.Н. Пирютко. - Минск: Аверсэв, 2004. - 416 с.

9) Шлыков. В.В. Геометрия: учебное пособие для 9-го класса учреждений, обеспечивающих получение общего среднего образования (базовый и повышенный уровни) / В.В. Шлыков. - 2-е издание. - Минск: Народная асвета, 2006. - 205 с.

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: