 |
Схема функционирования автоматического саморегулятора в цепи обратной связи
|
|
|
|
Системы автомат-го регулир-я (стабилизации), ведут свое начало от регулятора Уатта, созданного для автомат-й стабилизации числа оборотов выходного вала паровой машины (при изменяющейся внешней нагрузке на вал). Принцип, заложенный в этот регулятор, присущ всем системам автомат-й стабилизации в технике, в живых организмах (поддержание температуры тела др.).
В таких системах требуемое постоянное значение выходной переменной задается настройкой регулятора. Для осуществления процесса регулирования необходимы по крайней мере три основных блока: измерительный (Изм.), регулятор (РБ) и исполнительный (Исп.), расположенные в цепи обратной связи, присоединенной к объекту регулирования (ОР).
Измерит-ый блок служит для измерения фактич-го значения выходной перем-й OP y(t) и ее преобразования в сигнал, удобный для передачи в орган управления. Простейший РБ осуществляет сравнение двух величии - y0 которая определяется настройкой регулятора, и y(t) и вырабатывает сигнал 
,который с обратным знаком поступает в Исп. Если мощность этого сигнала недостаточна для приведения в действие Исп., то в цепь включают усилитель мощности. Исполнительный блок воздействует на вход управляемого объекта, увеличивая или уменьшая его интенсивность до величины, обеспечивающей требуемое значение выходной переменной.
59. Алгоритм численного решения модели динамического МОБа и экономическое содержание его параметров
1. Простейшая динамич. модель МОБа с пост-ми коэфф-ми выглядит так:
, (1)
- в-р-ст-ц объемов производства в году t 
(
);
- в-р-ст-ц абсол-х приростов произв-ва в году t (в-р-ст-ц производных функций);
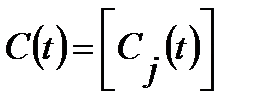- в-р-ст-ц потребл-я (включая непроизводств. потреблен-ие) в году t;
|
|
|
- матрица коэфф-ов прямых материал-х затрат;
- матрица коэфф-ов капиталоемкости приростов произв-ва.
2. Неоднородная система дифф-х уравн-й (1) эквивалентна системе:
, (2)
где 
- в-р-ст-ц конечн. использ-я продукции отраслей в году t, ();
- в-р-ст-ц абсол-х приростов конечной продукции по отраслям.
3. Матрица А продуктивна или неразложима, матрица F невырожденна 
, 
(поэлементно).
4.Решения системы (2) при 
в силу неотрицательности матриц 
и 
гарантируют, что 
, 
, 
.
5. Динам. модель замкнутой производственно – эконом. системы, представляющейсобой линейную однород. систему дифф.х уравн.й выглядит так
(3)
Решение системы (3) характ-т предельные технолог-е возможн-ти развития производства при задан. матрицах А и F, когда все ресурсы ВВП направляются на расширенное воспроизводство.
6. Общее решение системы (3) имеет следующий аналитический вид:
(4)
Параметры аналит-го решения (4) 
, 
, 
получаются в след. последовательности:
a) 
- корни характеристического уравнения n-го порядка.
(5)
б) 
- соответствующие 
собственные векторы матрицы , 
, и являются решениями (бесконечными) алгебраич-й системы однородных уравнений: 
, (6)
где, 0 (“нуль”) – нулевой вектор – столбец размерности 
;
в) 
- постоянные, определяемые из системы уравнений: 
(7)
где, Y(0) – в-р–с-ц конечн. использ-я продукции отраслей в базисном году.
В общем случае решение (7) содержит несколько отл-х от нуля компонент 
. Поэтому, единств. траектория системы (3), выходящая из начальной точки Y(0), представляет собой комбинацию экспонент, растущих с различными темпами.
7. Пусть 
. (где F - матрица коэфф-ов капиталоемкости приростов произв-ва.)
Для матрицы 
существует теорема Перрона:
а) матрица имеет положительное собственное число 
, которое превосходит модули всех остальных собственных чисел;
б) для , называемого корнем Фробениуса – Перрона, выполняется условие:
|
|
|
.
в) собственному числу отвечает единственный собственный вектор 
, все координаты которого строго положительны и удовлетворяют условию: 
8. Так как 
, 
, 
- соответствует вектор 
.
9. Значение 
в межотраслевой динамической модели находит объяснение технологического темпа прироста ВВП, а вектор 
- отраслевой структуры ВВП.
Содержание теоретических моделей роста и развития
Основные модели экономического роста.
Анализ экономического роста неизбежно должен был привести к созданию его моделей, без чего невозможно эффективное прогнозирование экономического роста и его последствий.
Современные модели экон. роста сформировались на основе двух источников –
1) кейнсианской теории макроэконом. равновесия и 2) неоклассической теории производства.
Эти два источника обусловили возникн-е 2х основных направлений в теорет-х исслед-х проблем эконом. роста - кейнсианского (позже неокейнсианского) и классического (позже неоклассического).
Основные современ. модели эконом. роста, как и любые модели предст-т собой абстрактное, упрощенное выраж-е реального эконом. процесса в форме уравн-й или графиков. Целый ряд допущений, предваряющих каждую модель, изначально отодвигает результат от реальных процессов, но, тем не менее, дает возможность проанализировать отдельные стороны и закономерности такого сложного явления как эконом. рост.
Большинство моделей роста исходят из того, что увеличение реал-го объема выпуска происходит, прежде всего, под влиянием роста основных факторов производств а труда (L) и капитала (К). Фактор «труд» обычно слабо поддается воздействию извне, тогда как величина K может быть скорректирована определенной инвест-й политикой. Как известно, запас K в экономике со временем сокращается на величину выбытия (амортизации) и увеличивается за счет роста чистых инвестиций. Очевидно, что эконом. рост ценен не сам по себе, а в качестве основы повышения благосостояния населения, поэтому качественная оценка роста часто дается через оценку динамики потребления.
Кейнс-е модели роста возникли в качестве развития и критической переработки кейнс-й модели макроэконом. равновесия. Наиболее известными являются неокейнсианские модели экономического роста Р. Харрода (Англия) и Е. Домара (США), которые основаны на двух предпосылках:
|
|
|
1) рост нац-го дохода является только функцией накопления капитала, а все остальные факторы (увеличение занятости, степень использования достижений НТП, улучшение организации производства), влияющие на рост капиталоотдачи, исключаются. Таким образом, модели Харрода и Домара - это однофакторные модели. Предполагается, что спрос на капитал при данной капиталоемкости зависит только от темпов роста нац. дохода;
2) капиталоемкость не зависит от соотношения цен производственных факторов, а определяется лишь техническими условиями производства.
Определяющим фактором экономического роста и его темпов, по мнению неокейнсианцев, является рост инвестиций. Инвестиции в рассматриваемой модели экономического роста играют важную роль: с одной стороны, они способствуют росту национального дохода, с другой - увеличивают производственные мощности. В свою очередь, рост дохода способствует увеличению занятости. Поскольку инвестиции увеличивают производственные мощности, постольку рост дохода должен быть достаточным, чтобы уравновесить увеличивающиеся производственные возможности общества, не допуская возникновения недогрузки предприятий и безработицы.
При анализе экономического роста неоклассики исходят из того, что:
1. стоимость продукции создается всеми производственными факторами;
2. каждый фактор производства вносит свой вклад в создание стоимости продукции в соответствии со всеми предельными продуктами и получает доход, равный этому предельному продукту;
3. существует количественная зависимость между выпуском продукции и ресурсами, необходимыми для ее производства, а также зависимость между самими ресурсами;
4. существует независимость факторов производства, их взаимозаменяемость. Модель неоклассиков в отличие от однофакторной неокейнсианской, является многофакторной.
Одной из важнейших моделей экономического роста является модель МОБа, построенная на основе метода «затраты - выпуск» американского экономиста В. Леонтьева.
|
|
|
В методе экономического анализа «затраты - выпуск» В. Леонтьев обращает прежде всего внимание на количественные связи в экономике. Это означает, что любое изменение потребностей или технологии производства какого-либо товара изменит структуру равновесных цен и тем самым приведет к изменению и технологических коэффициентов.
Таким образом, использование данного метода позволяет не только изучить взаимозависимость между различными отраслями экономики, проявляющуюся во взаимовлиянии цен, объемов производства, капиталовложений и доходов, но и осуществить прогнозир-е развития экономики страны, так как задавшись ростом одного или группы продуктов, можно определить масштабы роста остальных отраслей экономики страны, а тем самым и темпы экономического роста, его отраслевую структуру.
|
|
|
