 |
Раздел 1 физические основы механики
|
|
|
|
Основные формулы
Кинематика
Положение материальной точки в пространстве задается радиусом-вектором 
:
где 
- единичные векторы направлений (орты); х, у, z — координаты точки.
Средняя скорость
,
где 
- перемещение материальной точки за интервал времени 
.
Средняя путевая скорость
,
где 
- путь, пройденный точкой за интервал времени .
Мгновенная скорость
,
где 
, 
, 
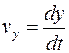- проекции скорости на оси координат.
Модуль скорости
.
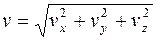Ускорение
,
где 
, 
, 
- проекции ускорения 
на оси координат.
Модуль ускорения
При криволинейном движении ускорение можно представить как сумму нормальной 
и тангенциальной 
составляющих:
Модули этих ускорений
,
где R - радиус кривизны в данной точке траектории.
Кинематическое уравнение равномерного движения материальной точки вдоль оси х
,
где x0 - начальная координата; t - время.
При равномерном движении v =const и a =0.
Кинематическое уравнение равнопеременного движения (а =const) вдоль оси x
,
где v 0 - начальная скорость; t - время.
Скорость точки при равнопеременном движении
.
Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением)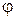 
.
Средняя угловая скорость
,
где Δφ - изменение угла поворота за интервал времени Δ t.
Мгновенная угловая скорость
.
Угловое ускорение
.
Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с осью вращения
Кинематическое уравнение равномерного вращения
,
где φ0 - начальное угловое перемещение; t - время. При равномерном вращении ω=const и ε=0.
|
|
|
Частота вращения
n=N/t,
или
n=1/T,
где N — число оборотов, совершаемых телом за время t; Т - период вращения (время одного полного оборота).
Кинематическое уравнение равнопеременного вращения (ε= const)
,
где ω0 - начальная угловая скорость; t - время.
Угловая скорость тела при равнопеременном вращении
.
Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами:
путь, пройденный точкой по дуге окружности радиусом R, при повороте на угол φ
;
линейная скорость точки
;
тангенциальное ускорение точки
:
нормальное ускорение точки
.
Динамика материальной точки и тела, движущегося
Поступательно
Уравнение движения материальной точки (второй закон Ньютона):
в векторной форме
и
,
где 
- геометрическая сумма сил, действующих на материальную точку; т - масса; а - ускорение; 
- импульс; N - число сил, действующих на точку;
в координатной форме (скалярной)
;
;
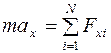или
;
;
,
где под знаком суммы стоят проекции сил 
на соответствующие оси координат.
Сила упругости
Fупр =- kx,
где k - коэффициент упругости (жесткость в случае пружины);
х - абсолютная деформация.
Сила гравитационного взаимодействия тел, рассматриваемых как материальные точки
,
где G - гравитационная постоянная; m1 и m2 - массы взаимодействующих тел; r - расстояние между ними.
Сила трения скольжения
F тр = μ N,
где μ - коэффициент трения скольжения; N - сила нормального давления.
Закон сохранения импульса
,
или
,
где N - число материальных точек (или тел), входящих в систему.
Работа, совершаемая постоянной силой
где α - угол между направлениями векторов силы 
и перемещения .
|
|
|
Работа, совершаемая переменной силой
,
где интегрирование ведется вдоль траектории, обозначаемой L.
Средняя мощность за интервал времени Δ t
.
Мгновенная мощность
,
или
,
где dA - работа, совершаемая за промежуток времени dt.
Кинетическая энергия материальной точки (или тела), движущейся поступательно
,
или
,
Потенциальная энергия тела WП и сила, действующая на тело в данной точке поля, связаны соотношением
,
или
,
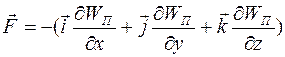где 
- единичные векторы (орты). В частном случае, когда поле сил обладает сферической симметрией (как, например, гравитационное),
.
Потенциальная энергия упругодеформированного тела (сжатой или растянутой пружины)
Потенциальная энергия гравитационного взаимодействия двух материальных точек (или тел) массами m 1, и т 2, находящихся на расстоянии r друг от друга
Потенциальная энергия тела, находящегося в однородном поле силы тяжести
где h - высота тела над уровнем, принятым за нулевой для отсчета потенциальной энергии.
Эта формула справедлива при условии h <<R, где R — радиус Земли.
Закон сохранения энергии в механике выполняется в замкнутой системе, в которой действуют только консервативные силы, и записывается в виде
WК+WП= const.
Применяя законы сохранения энергии и импульса к прямому центральному удару шаров, получаем формулу скорости шаров после абсолютно неупругого удара
и формулы скорости шаров после абсолютно упругого удара
,
,
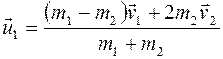где m 1 и m2 — массы шаров; v 1 и v 2 — их скорости до удара.
|
|
|
