Рекомендации по решению задач

 

Предложить единую схему решения задач невозможно, однако можно рекомендовать определенную последовательность действий. Приступая к решению задач по какому-либо разделу, необходимо ознакомиться с конкретными физическими понятиями и соотношениями этого раздела, разобрать приведенные примеры решения задач. При самостоятельном решении задач целесообразно придерживаться следующей схемы:

1) по условию задачи представьте себе физическое явление, о котором идет речь, сделайте краткую запись условия, выразив исходные данные в единицах СИ;

2) сделайте, если это необходимо, рисунок, поясняющий описываемый в задаче процесс;

3) напишите уравнение или систему уравнений, отображающих физический процесс;

4) преобразуйте уравнения так, чтобы в них входили лишь исходные данные и табличные величины;

5) решите задачу в общем виде;

6) произведите вычисления и оцените реальность числового ответа.

 

Примеры решения задач

Пример 1. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x=A+Bt+Ct³, где A =4 м, B =2 м/с, С =-0,5 м/с². Для момента времени t ₁=2 с определить: 1) координату x ₁ точки, 2) мгновенную скорость v ₁, 3) мгновенное ускорение a ₁.

Решение. 1. Координату точки, для которой известно кинематическое уравнение движения, найдем, подставив в уравнение движения вместо t заданное значение времени t ₁:

 

x=A+Bt+Ct ³.

 

Подставим в это выражение значения A, В, С, t ₁ и произведем вычисления:

 

x =(4+4- 0,5 2³) м=4 м.

 

2. Мгновенную скорость в произвольный момент времени найдем, продифференцировав координату х по времени:

 

.

 

Тогда в заданный момент времени t ₁ мгновенная скорость v ₁= B +3C t ₁². Подставим сюда значения В, С, t ₁ и произведем вычисления: v ₁ =- 4 м/с. Знак минус указывает на то, что в момент времени t₁=2 с точка движется в отрицательном направлении координатной оси.

3. Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты х по времени:

 

.

 

Мгновенное ускорение в заданный момент времени t ₁ равно a ₁ = 6 Ct ₁. Подставим значения С, t ₁и произведем вычисления:

a ₁=(-6 0,5 2) м/с=-6 м/с. Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.

 

Пример 2. При падении тела с большой высоты его скорость v _уст при установившемся движении достигает 80 м/с. Определить время τ, в течение которого начиная от момента начала падения скорость становится равной 1/2 v _уст. Силу сопротивления воздуха принять пропорциональной скорости тела.

Решение. На падающее тело действуют две силы: сила тяжести и сила сопротивления воздуха .

Сила сопротивления воздуха по условиям задачи пропорциональна скорости тела и противоположна ей по направлению:

 

,

 

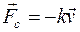где k - коэффициент пропорциональности, зависящий от размеров, формы тела и от свойств окружающей среды.

Напишем уравнение движения тела в соответствии со вторым законом Ньютона в векторной форме:

 

.

 

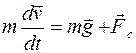Подставив выражение для , получим

 

.

 

Спроецируем все векторные величины на вертикально направленную ось и напишем уравнение для проекций:

 

 

После разделения переменных получим

 

 

Выполним интегрирование, учитывая, что при изменении времени от нуля до τ (искомое время) скорость возрастает от нуля до 1/2 v _уст

 

 

После интегрирования получаем

 

 

Подставим пределы интегрирования в левую часть равенства:

 

 

и найдем из полученного выражения искомое время:

 

 

Входящий сюда коэффициент пропорциональности k определим из следующих соображений. При установившемся движении (скорость постоянна) алгебраическая сумма проекций (на ось y) сил, действующих на тело, равна нулю, т. е. mg—kv _уст=0, откуда k=mg/v _уст. Подставим найденное значение k в полученную формулу для τ:

 

 

После сокращений и упрощений получим

 

 

Подставив в эту формулу значения v _уст, g, ln2 и произведя вычисления, получим τ=5,66 с.

 

Пример 3. Два шара массами m ₁=2,5 кг и m ₂=1,5 кг движутся навстречу друг другу со скоростями v ₁=6 м/с и v ₂ = 2 м/с. Определить: 1) скорость и шаров после удара; 2) кинетические энергии шаров W ₁ до и W ₂ после удара; 3) долю кинетической энергии w шаров, превратившейся во внутреннюю энергию. Удар считать прямым, неупругим.

Решение. 1. Неупругие шары не восстанавливают после удара своей первоначальной формы. Следовательно, не возникают силы, отталкивающие шары друг от друга, и шары после удара будут двигаться совместно с одной и той же скоростью и. Определим эту скорость по закону сохранения импульса. Так как шары движутся вдоль одной прямой, то этот закон можно записать в скалярной форме:

 

,

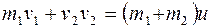откуда

 

.

 

Направление скорости первого шара примем за положительное; тогда при вычислении скорость второго шара, который движется навстречу первому, следует взять со знаком минус:

 

u =(2,5 6—1,5 2)/(2,5+1,5) м/с=3 м/с.

 

2. Кинетические энергии шаров до и после удара определим по формулам

 

; .

 

Произведя вычисления по этим формулам, получим

 

W ₁=(2,5 6²/2+1,5 2²/2)=48 (Дж); W ₂=(2,5+1,5) 3 ² =18 (Дж).

 

3. Сравнение кинетических энергий шаров до и после удара показывает, что в результате неупругого удара шаров произошло уменьшение их кинетической энергии, за счет чего увеличилась их внутренняя энергия. Долю кинетической энергии шаров, пошедшей на увеличение их внутренней энергии, определим из соотношения

 

; .

 

Пример 4. Платформа в виде диска радиусом R = 1,5 м и массой m ₁ = 180 кг вращается по инерции около вертикальной оси с частотой n =10 мин^-1. В центре платформы стоит человек массой т ₂=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?

Решение. По закону сохранения момента импульса,

 

,

 

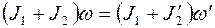где J ₁ - момент инерции платформы; J ₂ - момент инерции человека, стоящего в центре платформы; - угловая скорость платформы с человеком, стоящим в ее центре; J₂' - момент инерции человека, стоящего на краю платформы; ω' - угловая скорость платформы с человеком, стоящим на ее краю.

Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением

 

.

 

Определив отсюда ω' и подставив полученное выражение в формулу закона сохранения момента импульса, будем иметь

 

v=(J ₁ +J ₂ )ω R/(J ₁ +J' ₂)

 

Момент инерции платформы рассчитываем как для диска; следовательно, . Момент инерции человека рассчитываем как для материальной точки. Поэтому J ₂=0, J' ₂ =m ₂ R ². Угловая скорость платформы до перехода человека равна ω=2π n.

Заменив в формуле скорости величины J ₁, J ₂, J' ₂. и ω их выражениями, получим

 

 

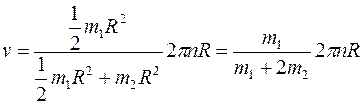
Сделав подстановку значений т ₁, т ₂, п, R и π, найдем линейную скорость человека:

(м/с).

 

Пример 5. Кинетическая энергия W_K электрона равна 1 МэВ. Определить скорость электрона.

Решение. Релятивистская формула кинетической энергии

 

 

где E ₀= m ₀ c ² - энергия покоя электрона.

Выполнив относительно β преобразования, найдем скорость частицы, выраженную в долях скорости света (β= v / c):

 

.

 

Вычисления по этой формуле можно производить в любых единицах энергии, так как наименования единиц в правой части формул сократятся, и в результате подсчета будет получено отвлеченное число.

Подставив числовые значения Е ₀и W_K в мегаэлектрон-вольтах, получим β =0,941.

Так как v= β c, то v =0,941∙3∙10⁸= 2,82·10⁸ (м/с).

Чтобы определить, является ли частица с кинетической энергией W_K релятивистской или классической, достаточно сравнить кинетическую энергию частицы с ее энергией покоя. Если <<1, частицу можно считать классической.

 

Пример 6. Материальная точка массой т =5 г совершает гармонические колебания с периодом Т =2 с. Амплитуда колебаний A =3 см. Определить: 1) скорость v точки в момент времени, когда смещение х= 1,5 см; 2) максимальную силу F_max, действующую на точку.

Решение. 1. Уравнение гармонического колебания имеет вид

 

 

а формулу скорости получим, взяв первую производную по времени от смещения:

 

 

Чтобы выразить скорость через смещение, надо исключить из формул время. Для этого возведем оба уравнения в квадрат, разделим первое на А², второе на A ²ω ² и сложим:

 

 

Решив последнее уравнение относительно v, найдем

 

 

Поскольку , получаем

 

Выполнив вычисления, получим 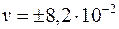м/c

Знак плюс соответствует случаю, когда направление скорости совпадает с положительным направлением оси х, знак минус – случаю, когда направление скорости совпадает с отрицательным направлением оси х.

2. Силу, действующую на точку, найдем по второму закону Ньютона:

 

 

где а - ускорение точки, которое получим, взяв производную по времени от скорости:

 

 

Подставив выражение ускорения в формулу второго закона Ньютона, получим

 

 

Отсюда максимальное значение силы

 

 

Подставив в это уравнение значения величин π, T, т и A, найдем Н.

 

Пример 7. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых , , где А ₁ = 1 см, A ₂=2 см, ω=π с^-1. Найти уравнение траектории точки.

Решение. Чтобы найти уравнение траектории точки, исключим время t из заданных уравнений. Для этого воспользуемся формулой

 

 

В данном случае α=ω t, поэтому

 

 

Как следует из условия задачи, , и уравнение траектории

 

.

 

Полученное выражение представляет собой уравнение параболы, ось которой совпадает с осью Ох. Из уравнений, заданных в условии задачи, следует, что смещение точки по осям координат ограничено и заключено в пределах от -1 до +1 см по оси Ох и от -2 до +2 см по оси Оу.

 

Пример 8. Найти молярную массу М смеси кислорода массой m ₁=25 г и азота массой m ₂=75 г.

Решение. Молярная масса смеси М _см есть отношение массы смеси т _см к количеству вещества смеси υ_см т.е.

 

M_см=m_см/υ_см

 

Масса смеси равна сумме масс компонентов смеси m _см= m ₁+ m ₂. Количество вещества смеси равно сумме количеств вещества компонентов.

Подставив в формулу (1) выражения m _см и υ_см, получим

 

 

Молярные массы M ₁ кислорода и М ₂, азота: M ₁ =32×10^-3 кг/моль, М ₂=28×10^-3 кг/моль. Подставим значения величин и произведем вычисления:

 

(кг/моль)

 

Пример 9. В баллоне объемом V =10 л находится гелий под давлением p ₁=l МПа при температуре T ₁=300 К. После того как из баллона был израсходован гелий массой m =10 г, температура в баллоне понизилась до T ₂=290 К. Определить давление p ₂ гелия, оставшегося в баллоне.

Решение. Для решения задачи воспользуемся уравнением Клапейрона - Менделеева, применив его дважды к начальному и конечному состояниям газа. Для начального состояния уравнение имеет вид

 

p ₁ V = RT₁,

 

а для конечного состояния –

 

p₂V= RT₂,

 

где m ₁ и m ₂ - массы гелия в начальном и конечном состояниях.

Выразим массы m ₁ и m ₂ гелия:

 

;

 

и вычтем m ₂ из m ₁:

 

 

Отсюда найдем искомое давление:

 

 

Подставив значения величин, получим р₂ =3,64∙10⁵ Па

Пример 10. Найти среднюю кинетическую энергию одной молекулы аммиака NH ₃ при температуре t =27° С и среднюю энергию вращательного движения этой молекулы при той же температуре.

Решение. Средняя полная энергия молекулы определяется по формуле

 

 

где i - число степеней свободы молекулы; k - постоянная Больцмана; Т - термодинамическая температура газа: T = t + Т ₀, где Т ₀=273 К.

Число степеней свободы i четырехатомной молекулы, какой является молекула аммиака, равно 6.

Подставив значения величин, получаем

 

Дж.

 

Средняя энергия вращательного движения молекулы определяется по формуле

 

 

где число 3 означает число степеней свободы поступательного движения.

Подставим значения величин и вычислим:

 

Дж.

Пример 11. Средняя длина свободного пробега < l > молекулы углекислого газа при нормальных условиях равна 40 нм. Определить среднюю арифметическую скорость < v > молекул и число z соударений, которые испытывает молекула в 1 с.

Решение. Средняя арифметическая скорость молекул определяется по формуле

 

 

где М - молярная масса вещества.

Подставив числовые значения, получим < v >=362 м/с.

Среднее число z соударений молекулы в 1 с определяется отношением средней скорости < v > молекулы к средней длине ее свободного пробега < l >:

 

.

Подставив в эту формулу значения < v >=362 м/с, < l >=40 нм=4×10^{-8 м, получим} z = 9,05×10⁹ с^-1.

 

Пример 12. Определить изменение D S энтропии при изотермиче­ском расширении кислорода массой m =10 г от объема V ₁=25 л до объема V ₂=100 л.

Решение. Так как процесс изотермический, то в общем выражении энтропии температуру выносят за знак интеграла. Выполнив это, получим

 

 

Количество теплоты Q, полученное газом, найдем по первому началу термодинамики: Q= D U+A. Для изотермического процесса D U =0, следовательно, Q=A, а работа А для этого процесса определяется по формуле

 

 

С учетом этого получаем

 

 

Подставив числовые значения и произведя вычисления, получим

 

DS=(10×10^-3/(32×10^-3)) ×8,31 ln(100×10^-3 / (25×10^-3))=3,60 (Дж/К).

 

ЗАДАЧИ

 

1. Три четверти своего пути автомобиль прошел со скоростью v ₁=60 км/ч, остальную часть пути - со скоростью v ₂ = 80 км/ч. Какова средняя путевая скорость < v > автомобиля?

2. Первую половину пути тело двигалось со скоростью v ₁=2 м/с, вторую - со скоростью v ₂=8 м/с. Определить среднюю путевую скорость < v >.

3. Движение материальной точки задано уравнением x=At+Bt², где A =4 м/с, В= - 0,05 м/с². Определить момент времени, в который скорость v точки равна нулю. Найти координату и ускорение в этот момент.

4. Движения двух материальных точек выражаются уравнениями: x ₁ =A ₁ +B ₁ t+C ₁ t², x ₂ =A ₂ +B ₂ t+C ₂ t², где A ₁=20 м, A ₂=2 м, B ₁ =B ₂ = 2 м/с, C ₁= - 4 м/с², С ₂=0,5 м/с². В какой момент времени t скорости этих точек будут одинаковыми? Определить скорости v ₁ и v ₂ и ускорения a ₁ и а ₂ точек в этот момент.

5. Две материальные точки движутся согласно уравнениям: x ₁ =A ₁ t+B ₁ t ² +C ₁ t ³, x ₂ =A ₂ t+B ₂ t ² +C ₂ t ³, где A ₁=4 м/c, B ₁=8 м/с², C ₁=- 16 м/с³, A ₂=2 м/с, B ₂ = - 4 м/с², С ₂=1м/с³. В какой момент времени t ускорения этих точек будут одинаковы? Найти скорости v ₁ и v ₂ точек в этот момент.

6. Камень брошен вертикально вверх с начальной скоростью v ₀=20 м/с. Через какое время камень будет находиться на высоте h =15м? Найти скорость v камня на этой высоте. Сопротивлением воздуха пренебречь. Принять g =10 м/с².

7. Вертикально вверх с начальной скоростью v ₀=20 м/с брошен камень. Через τ=1 с после этого брошен вертикально вверх другой камень с такой же скоростью. На какой высоте h встретятся камни?

8. Движение точки по прямой задано уравнением x=At+Bt², где A =2 м/с, В= - 0,5 м/с². Определить среднюю путевую скорость < v> движения точки в интервале времени от t ₁=l с до t ₂=3 с.

9. Точка движется по прямой согласно уравнению x=At+Bt³, где A =6 м/с, В = - 0,125 м/с³. Определить среднюю путевую скорость < v> точки в интервале времени от t ₁=2 с до t ₂=6 с.

10. Тело, брошенное вертикально вверх, находилось на одной и той же высоте h= 8,6 м два раза с интервалом D t= 3 с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела.

11. Движение материальной точки задано уравнением , где A =10 м, В = - 5 м/с², С =10 м/с. Найти выражения для скорости и ускорения . Для момента времени t =1с вычислить: 1) модуль скорости 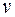; 2) модуль ускорения 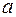; 3) модуль тангенциального ускорения ; 4)модуль нормального ускорения .

12. Движение точки по окружности радиусом R =4 м задано уравнением S = A+Bt+Ct², где A =10 м, В =-2 м/с, С =1 м/с². Найти тангенциальное а , нормальное a_n и полное а ускорения точки в момент времени t =2с.

13. По дуге окружности радиусом R= 10 м движется точка. В некоторый момент времени нормальное ускорение точки а_n =4,9 м/с²; в этот момент векторы полного и нормального ускорений образуют угол φ=60°. Найти скорость v и тангенциальное ускорение a точки.

14. Точка движется по окружности радиусом R=2 м согласно уравнению S = At³, где A =2 м/с³. В какой момент времени t нормальное ускорение а_n точки будет равно тангенциальному а ?Определить полное ускорение а в этот момент.

15. Движение точки по кривой задано уравнениями x=A ₁ t ³ и y = A ₂ t, где A ₁=l м/с³, A ₂=2 м/с. Найти уравнение траектории точки, ее скорость v и полное ускорение а в момент времени t= 0,8 с.

16. Камень брошен с вышки в горизонтальном направлении с начальной скоростью v ₀=30 м/с. Определить скорость v, тангенциальное a и нормальное a_n ускорения камня в конце второй секунды после начала движения.

17. Диск радиусом R =20 см вращается согласно уравнению φ= A+Bt+Сt ³, где A =3 рад, В =-1 рад/с, С =0,1 рад/с³. Определить тангенциальное a нормальное а_n и полное а ускорения точек на окружности диска для момента времени t =10 с.

18. Колесо автомашины вращается равноускоренно. Сделав N =50 полных оборотов, оно изменило частоту вращения от n ₁=4 с¹ до n ₂=6 с¹. Определить угловое ускорение e и время вращения Δ t колеса.

19. Диск вращается с угловым ускорением ε = - 2 рад/с². Сколько оборотов N сделает диск при изменении частоты вращения от n ₁=240 мин^-1 до n ₂=90 мин^-1? Найти время Δ t, в течение которого это произойдет.

20. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R= 50 м. Уравнение движения автомобиля имеет вид S (t) = A+Bt+Ct², где A =10 м, B =10 м/с, С =-0,5 м/с². Найти скорость v автомобиля, его тангенциальное a _τ, нормальное а_n. и полное а ускорения в момент времени t =5 с.

21. Два бруска массами m ₁=l кг и m ₂=4 кг, соединенные шнуром, лежат на столе. С каким ускорением а будут двигаться бруски, если к одному из них приложить силу F =10 H, направленную горизонтально? Какова будет сила натяжения Т шнура, соединяющего бруски, если силу F =10 Н приложить к первому бруску? ко второму бруску? Трением пренебречь.

22. Наклонная плоскость, образующая угол α=25° с плоскостью горизонта, имеет длину l=2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время t =2 с. Определить коэффициент трения μ тела о плоскость.

23. Материальная точка массой т= 2 кг движется под действием некоторой силы F согласно уравнению x=A+Bt+Ct²+Dt ³, где С =1 м/с², D=- 0,2 м/с³. Найти значения этой силы в моменты времени t ₁ =2 с и t ₂=5 с. В какой момент времени сила равна нулю?

24. Шарик массой m =300 г ударился о стену и отскочил от нее. Определить импульс p ₁, полученный стеной, если в последний момент перед ударом шарик имел скорость v ₀=10 м/с, направленную под углом α=30° к поверхности стены. Удар считать абсолютно упругим.

25. Автоцистерна с керосином движется с ускорением а =0,7 м/с². Под каким углом α к плоскости горизонта расположен уровень керосина в цистерне?

26. Бак в тендере паровоза имеет длину l =4 м. Какова разность Δ l уровней воды у переднего и заднего концов бака при движении поезда с ускорением a =0,5 м/с²?

27. Катер массой m =2 т с двигателем мощностью N =50 кВт развивает максимальную скорость v _mах =25 м/с. Определить время τ, в течение которого катер после выключения двигателя потеряет половину своей скорости. Принять, что сила сопротивления движению катера изменяется пропорционально квадрату скорости.

28. Снаряд массой т= 10 кг выпущен из зенитного орудия вертикально вверх со скоростью v ₀=800 м/с. Считая силу сопротивления воздуха пропорциональной скорости, определить время t подъема снаряда до высшей точки. Коэффициент сопротивления k =0,25 кг/с.

29. С вертолета, неподвижно висящего на некоторой высоте над поверхностью Земли, сброшен груз массой m =100 кг. Считая, что сила сопротивления воздуха изменяется пропорционально скорости, определить, через какой промежуток времени Δ t ускорение а груза будет равно половине ускорения свободного падения. Коэффициент сопротивления k =10 кг/с.

30. Моторная лодка массой m =400 кг начинает двигаться по озеру. Сила тяги F мотора равна 0,2 кН. Считая силу сопротивления F _c пропорциональной скорости, определить скорость v лодки через Δ t =20 с после начала ее движения. Коэффициент сопротивления k =20 кг/с.

31. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса человека М = 60 кг, масса доски т= 20 кг. С какой скоростью и (относительно пола) будет двигаться тележка, если человек пойдет вдоль доски со скоростью (относительно доски) v= 1 м/с? Массой колес пренебречь. Трение во втулках не учитывать.

32. В лодке массой m ₁=240 кг стоит человек массой m ₂=60 кг. Лодка плывет со скоростью v ₁=2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью v =4 м/с (относительно лодки). Найти скорость и движения лодки после прыжка человека в двух случаях: 1) человек прыгает вперед по движению лодки и 2) в сторону, противоположную движению лодки.

33. Диск радиусом R=40 см вращается вокруг вертикальной оси. На краю диска лежит кубик. Принимая коэффициент трения μ=0,4, найти частоту п вращения, при которой кубик соскользнет с диска.

34. Автомобиль идет по закруглению шоссе, радиус R кривизны которого равен 200 м. Коэффициент трения μ колес о покрытие дороги равен 0,1 (гололед). При какой скорости v автомобиля начнется его занос?

35. Материальная точка массой m =2 кг двигалась под действием некоторой силы, направленной вдоль оси Ох согласно уравнению x=A+Bt+Ct ² +Dt³, где В = - 2 м/с, С =1 м/с², D = - 0,2 м/с³. Найти мощность N, развиваемую силой в момент времени t ₁=2 с и t ₂=5 с.

36. Мотоциклист едет по горизонтальной дороге. Какую наименьшую скорость v он должен развить, чтобы, выключив мотор, проехать по треку, имеющему форму «мертвой петли» радиусом R =4 м? Трением и сопротивлением воздуха пренебречь.

37. Конькобежец, стоя на льду, бросил вперед гирю массой m ₁=5 кг и вследствие отдачи покатился назадсо скоростью v ₂=1 м/с. Масса конькобежца m ₂=60 кг. Определить работу A, совершенную конькобежцем при бросании гири.

38. Два неупругих шара массами m ₁=2 кг и m ₂=3 кг движутся со скоростями соответственно v ₁=8 м/с и v ₁=4 м/с. Определить увеличение D U внутренней энергии шаров при их столкновении в двух случаях: 1) меньший шар нагоняет больший; 2) шары движутся навстречу друг другу.

39. Шар массой m ₁, летящий со скоростью v ₁=5 м/с, ударяет неподвижный шар массой m ₂. Удар прямой, неупругий. Определить скорость и шаров после удара, а также долю ω кинетической энергии летящего шара, израсходованной на увеличение внутренней энергии этих шаров. Рассмотреть два случая: 1) т ₁ = 2 кг, m ₂=8 кг; 2) m ₁=8 кг, m ₂=2 кг.

40. Шар массой m ₁=200 г, движущийся со скоростью v ₁=10 м/с, ударяет неподвижный шар массой m ₂=800 г. Удар прямой, абсолютно упругий. Каковы будут скорости v ₁ и v ₂ шаров после удара?

41. Вычислить момент инерции J проволочного прямоугольни­ка со сторонами а =12 см и b =16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью τ=0,1 кг/м.

42. Определить момент инерции J кольца массой т =50 г и радиусом R =10 см относительно оси, лежащей в плоскости кольца и касательной к нему.

43. Диаметр диска d =20 см, масса т =800 г. Определить момент инерции J диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска.

44. Найти момент инерции J плоской однородной прямоугольной пластины массой т =800 г относительно оси, совпадающей с одной из ее сторон, если длина а другой стороны равна 40 см.

45. Определить момент инерции J тонкой плоской пластины со сторонами а =10 см и b =20 см относительно оси, проходящей через центр масс пластины параллельно большей стороне. Масса пластины равномерно распределена по ее площади с поверхностной плотностью σ=1,2 кг/м².

46. Тонкий однородный стержень длиной l =50 см и массой m =400 г вращается с угловым ускорением ε=3 рад/с² около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент М.

47. Вал массой m =100 кг и радиусом R= 5см вращался с частотой n =8 с^-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F =40 H, под действием которой вал остановился через t =10 с. Определить коэффициент трения μ.

48. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузики массой m ₁=100 г и т ₂=110 г. С каким ускорением а будут двигаться грузики, если масса т блока равна 400 г? Трение при вращении блока ничтожно мало.

49. Шар массой m =10 кг и радиусом R =20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид φ= A+Bt²+Ct ³, где В =4 рад/с², С = - 1 рад/с³. Найти закон изменения момента сил, действующих на шар. Определить момент сил М в момент времени t= 2с.

50. Через неподвижный блок массой т =0,2 кг перекинут шнур, к концам которого подвесили грузы массами m₁= 0,3кг и m₂=0,5 кг. Определить силы натяжения T ₁ и T ₂ шнура по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу.

51. Человек стоит на скамье Жуковского и ловит рукой мяч массой m =0,4 кг, летящий в горизонтальном направлении со скоростью v =20 м/с. Траектория мяча проходит на расстоянии r =0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью w начнет вращаться скамья Жуковского с человеком, поймавшим мяч, если суммарный момент инерции J человека и скамьи равен 6 кг·м²?

52. Шарик массой т= 100 г, привязанный к концу нити длиной l ₁=l м, вращается, опираясь на горизонтальную плоскость, с частотой n ₁=1 с^-1. Нить укорачивается и шарик приближается к оси вращения до расстояния l ₂=0,5 м. С какой частотой n ₂ будет при этом вращаться шарик? Какую работу А совершит внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.

53. Маховик вращается по закону, выраженному уравнением φ =A+Bt+Ct², где A =2 рад, B =32 рад/с, С = - 4 рад/с². Найти среднюю мощность < N>, развиваемую силами, действующими на маховик при его вращении, до остановки, если его момент инерции J =100 кг·м².

54. Маховик в виде диска массой m =80 кг и радиусом R= 30см находится в состоянии покоя. Какую работу A ₁нужно совершить, чтобы сообщить маховику частоту n =10 с^-1? Какую работу A ₂ пришлось бы совершить, если бы при той же массе диск имел меньшую толщину, но вдвое больший радиус?

55. Маховик, момент инерции J которого равен 40 кг·м², начал вращаться равноускоренно из состояния покоя под действием момента силы М =20 Н·м. Вращение продолжалось в течение t= 10 с. Определить кинетическую энергию, приобретенную маховиком.

56. Обруч и сплошной цилиндр, имеющие одинаковую массу т =2 кг, катятся без скольжения с одинаковой скоростью v =5 м/с. Найти кинетические энергии W ₁ и W ₂ этих тел.

57. Шар катится без скольжения по горизонтальной поверхности. Полная кинетическая энергия Т шара равна 14 Дж. Определить кинетическую энергию поступательного и вращательного движения шара.

58. Определить линейную скорость v центра шара, скатившегося без скольжения с наклонной плоскости высотой h= 1м.

59. Сколько времени t будет скатываться без скольжения обруч с наклонной плоскости длиной l =2 м и высотой h =10 см?

60. Тонкий прямой стержень длиной l= 1м прикреплен к горизонтальной оси, проходящей через его конец. Стержень отклонили на угол φ=60° от положения равновесия и отпустили. Определить линейную скорость v нижнего конца стержня в момент прохождения через положение равновесия.

61. Фотонная ракета движется относительно Земли со скоро­стью v =0,6 с. Во сколько раз замедлится ход времени в ракете с точки зрения земного наблюдателя?

62. Собственное время жизни τ₀ мю-мезон

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: