 |
Физические основы термодинамики
|
|
|
|
Связь между молярной (Cm) и удельной (с) теплоемкостями газа
Cm=cM,
где М - молярная масса газа.
Молярные теплоемкости при постоянном объеме и постоянном давлении соответственно равны
 ,
,
где i - число степеней свободы; R - молярная газовая постоянная.
Уравнение Майера
 .
.
Удельные теплоемкости при постоянном объеме и постоянном давлении соответственно равны
 ,
,  .
.
Показатель адиабаты
 , или
, или 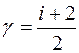 .
.
Внутренняя энергия идеального газа
 , или
, или  ,
,
где <e> - средняя кинетическая энергия молекулы; N - число молекул газа; ν - количество вещества.
Работа, связанная с изменением объема газа, в общем случае вычисляется по формуле
 ,
,
где V 1 - начальный объем газа; V 2 - его конечный объем.
Работа газа:
а) при изобарном процессе (p =const)
A = p (V 2 - V 1);
б) при изотермическом процессе (T =const)

в) при адиабатном процессе
 , или
, или  ,
,
где T 1 - начальная температура газа; T 2 - его конечная температура.
Уравнение Пуассона (уравнение газового состояния при адиабатном процессе)
 .
.
Связь между начальным и конечным значениями параметров состояний газа при адиабатном процессе:
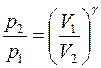 ;
; 
 ;
;  .
.
Первое начало термодинамики в общем случае записывается в виде
Q =D U + A,
где Q - количество теплоты, сообщённое газу; D U - изменение его внутренней энергии; А - работа, совершаемая газом против внешних сил.
Первое начало термодинамики:
а) при изобарном процессе
 ;
;
б) при изохорном процессе (A =0)
 ;
;
в) при изотермическом процессе (D U =0)
 ;
;
г) при адиабатном процессе (Q =0)

 .
.
Термический коэффициент полезного действия (КПД) цикла в общем случае
|
|
|
 ,
,
где Q 1 - количество теплоты, полученное рабочим телом (газом) от нагревателя; Q 2 - количество теплоты, переданное рабочим телом охладителю.
КПД цикла Карно
 , или
, или  ,
,
где T 1 - температура нагревателя; T 2 - температура охладителя.
Изменение энтропии
 ,
,
где A и B - пределы интегрирования, соответствующие начальному и конечному состояниям системы. Так как процесс равновесный, то интегрирование проводится по любому пути.
Формула Больцмана
S=k ×ln W,
где S - энтропия системы; W - термодинамическая вероятность ее состояния; k - постоянная Больцмана.
Реальные газы. Жидкости.
Уравнение Ван-дер-Ваальса для одного моля газа
 ,
,
для произвольного количества вещества ν газа
 ,
,
где a и b - постоянные Ван-дер-Ваальса (рассчитанные на один моль газа); V - объем, занимаемый газом; Vm - молярный объем; р - давление газа на стенки сосуда.
Внутреннее давление, обусловленное силами взаимодействия молекул,
 , или
, или  .
.
Связь критических параметров – объема, давления и температуры газа – с постоянными а и b Ван-дер-Ваальса:
 ;
;  ;
;  .
.
Внутренняя энергия реального газа
 ,
,
где СV - молярная теплоемкость газа при постоянном объеме.
Поверхностное натяжение
σ=F/l,
где F - сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости, или
 ,
,
где ΔW - изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади ΔS поверхности этой пленки.
Формула Лапласа в общем случае записывается в виде
 ,
,
где р – давление, создаваемое изогнутой поверхностью жидкости;
σ - поверхностное натяжение; R1 и R2 – радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости.
В случае сферической поверхности
 .
.
Высота подъема жидкости в капиллярной трубке
|
|
|
 ,
,
где θ - краевой угол; R - радиус канала трубки; р - плотность жидкости; g - ускорение свободного падения.
Высота подъема жидкости между двумя близкими и параллельными плоскостями
 ,
,

где d - расстояние между плоскостями.
|
|
|


