 |
Фундаментальные физические постоянные
|
|
|
|
Фундаментальные физические постоянные
| Величина | Символ | Значение | Размерность |
| Скорость света в вакууме | c | 299 792 458 (точно) | м× с–1 |
| Постоянная Планка | h | 6, 626 075  10–34
| Дж× с |
| Элементарный заряд | e | 1, 602 177 10–19
| Кл |
| Число Авогадро | NA | 6, 022 137 1023
| моль–1 |
| Константа Больцмана | k | 1, 380 658 10–23
| Дж× К–1 |
| Газовая постоянная | R | 8, 314 510 1, 987 216 0, 082 058 | Дж× К–1× моль–1 кал× К–1× моль–1 л× атм. × К–1× моль–1 |
| Постоянная Фарадея | F | 96 485, 31 | Кл× моль–1 |
| Стандартное ускорение свободного падения | g | 9, 806 65 (точно) | м× с–2 |
Занятие № 1.
План занятия:
1. Техника безопасности при работе в лаборатории «Физической и коллоидной химии».
2. Законы идеальных газов.
3. Решение задач на тему «Законы идеальных газов».
1. Техника безопасности при работе в лаборатории «Физической и коллоидной химии».
2. Законы идеальных газов.
Газовые законы
Состояние газа определяется тремя параметрами: давлением (Р), температурой (Т) и объемом (V). Взаимосвязь этих параметров для определенного количества газа выражается газовыми законами.
1. Закон Бойля – Мариотта: при постоянной температуре для заданного количества газа его давление пропорционально объему:
PV = Const или P1V1 = P2V2 для состояния 1 и 2
2. Закон Гей – Люссака: при постоянном давлении объем заданного количества газа пропорционален его абсолютной температуре:
V = c(t + 273), где с – постоянная величина, или 
для состояний 1 и 2.
3. Закон Шарля: при постоянном объеме давление заданного количества газа пропорционально его абсолютной температуре:
Р = c(t + 273), где с – постоянная величина, или 
для состояний 1 и 2.
|
|
|
Соотношение всех трех параметров для двух состояний 1 и 2 определенного количества газа показывает объединенный газовый закон:
, причем, какой это газ или смесь газов не имеет значения.
Так по закону Авогадро в равных объемах различных газов при одинаковых условиях содержится одинаковое число молекул.
Если состояние 2 отвечает нормальным условиям (Т = 273, 15 К, Р = 101, 3·103 Па), состояние «0» (ноль), то объединенный газовый закон принимает вид: 
.
Из закона Авогадро можно вывести следствия:
1. Один моль газообразного вещества содержит одинаковое число структурных единиц, которое называется числом Авогадро (Na = 6, 02 · 1023). Это следствие справедливо для веществ в любом агрегатном состоянии.
2. Один моль любого газообразного вещества при одинаковых условиях занимает одинаковый объем. Эксперимент показал, что этот объем при нормальных условиях равен 22, 4 л (в СИ 22, 4 · 10-3 м3). Его называют молярным объемом газообразного вещества при нормальных условиях (VМ, О = 22, 4 л/моль = 22, 4 · 10-3 м3/моль).
Для одного моль газа правая часть объединенного газового закона принимает конкретную величину:
, где величина R – универсальная газовая постоянная.
Объединенный газовый закон для n моль газа можно записать так:
или 
Это выражение называется уравнение Клапейрона – Менделеева.
Закон дальтона: общеедавление смеси газов равно сумме парциальных давлений составных частей (компонентов):
Р = P1+ Р2 + … + Рk
где Р – общее давление смеси газов, P1, P2 – парциальные давления компонентов смеси. Парциальным давлением называется давление каждого компонента, если бы он один занимал объем, равный объему смеси при той же температуре.
Зависимость между парциальными давлениями и общим выражается уравнениями:
Таким образом, парциальное давление каждого компонента равно произведению его мольной доли на общее давление смеси.
|
|
|
Для идеальных газов мольная доля cравна объемной доле φ.
Кинетическая теория газов. Основным уравнением кинетической теории газов для одного моль является уравнение:
PV=1/3NAmu2
где т – масса молекулы; и – средняя квадратичная скорость молекул; NA – число молекул в одном моль. Для любого количества вещества в уравнение вместо NА входит N. Из основного уравнения кинетической теории газов можно вывести изложенные выше газовые законы и некоторые новые положения.
Для одного моль газа: 1/3NAmu2 = RT
Отсюда средняя квадратичная скорость молекул:
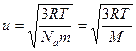, где М = Nат – масса одного моль газа.
Из этого уравнения следует, что для одного и того же газа средняя квадратичная скорость молекул прямо пропорциональна корню квадратному из абсолютной температуры:
, где u1 – средняя квадратичная скорость при температуре T1, а и2 – при Т2. Для различных газов при одинаковой температуре средняя квадратичная скорость молекул обратно пропорциональна корню квадратному из молекулярных масс:
, где и1 и М1 относятся к первому газу, а u2 и М2 – ко второму.
NАmu2/2=3/2RT.
Выражение, стоящее в левой части этого равенства, есть средняя кинетическая энергия поступательного движения молекул одного моль идеального газа. Обозначив ее через Е -
E=3/2RT.
Средняя кинетическая энергия поступательного движения одной молекулы газа равна:
e = 3/2kT, где k = R/N постоянная Больцмана.
Следовательно, кинетическая энергия идеального газа пропорциональна абсолютной температуре.
|
|
|
