 |
Моделирование электрической сети
|
|
|
|
При проектировании составляется расчётная схема электрической сети, для которой проводится оптимизация развития. Существующая сеть может быть представлена упрощённо. Кроме существующей сети на схеме отображаются все альтернативные перспективные объекты. На рис. 5.3 существующие объекты показаны сплошными линиями, новые – штриховыми.
Для математического описания схем сетей используются графы, представляющие собой совокупность ветвей (дуг) и узлов (вершин). Ветви графа сети на рис. 5.3 представляют собой существующие и все намечаемые к строительству элементы сети, а его узлы – сборные шины или электрические узлы.
|
| Рис.5.3. Расчётный граф сети |
В примере, приведённом на рис. 5.3, новыми ветвями являются подстанции в узлах у =4 и у =6 (ветви в =4, в =17), а также новая распределительная линия между узлами у =9 и у =10. Для усиления основной сети предусматриваются новые линии. Если они временно будут использоваться на напряжении распределительной сети, то им соответствуют ветви в =3 и в =15. Ветви в =2 и в =16 – это те же линии, но сразу на напряжении основной сети. Центрами питания рассматриваемой сети являются узлы у =1 и у =12.
Для выполнения технических и экономических расчётов на ЭВМ каждая ветвь идентифицируется номерами узлов её начала и конца. Необходимые для расчётов показатели ветви определяются по формулам:
,
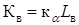где 
, 
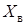– активное и реактивное сопротивления ветви длиной 
(для трансформаторной ветви =1);
, 
– погонные сопротивления ветви;
– капиталовложения для ветви графа сети;
– удельные капиталовложения для ветви.
Величина α обозначает состояние, в котором может находиться ветвь графа. В простейшем случае каждая ветвь может находиться в одном из двух состояний: ветвь отсутствует или имеет некоторое фиксированное значение , , 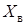. Число возможных вариантов сети, содержащей m новых ветвей, будет равно
|
|
|
.
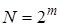Некоторые ветви могут вводиться только совместно и образовывать группу ветвей. На рис. 5.3 группой ветвей являются ветви в =2 и в =4 или в =16 и в =17. С другой стороны некоторые ветви или их группы являются взаимоисключающими. Например, ветвь в =3 и группа в =2, в =4 не могут быть сооружены одновременно. Эти обстоятельства несколько уменьшают число возможных вариантов сети N.
Технический анализ значительного множества вариантов сети в приемлемые для проектировщика сроки предопределяет применение упрощённых методов расчёта нормальных и послеаварийных режимов сети. Достаточно часто в оптимизационных моделях электрических сетей для расчёта потокораспределения активной мощности используется так называемая модель постоянного тока. В такой модели приближённо учитываются первый и второй законы Кирхгофа. Такое упрощение основано на следующем. Векторная диаграмма напряжений ветви электрической сети (рис. 5.4, а) для реальных сетей, как правило, близка к следующим двум предельным случаям.
В первом случае для системообразующих сетей напряжением 220 кВ и выше реактивное сопротивление ветви значительно больше активного. Падение напряжения в ветви ij 
по модулю равно 
, а модули напряжения в начале и конце ветви примерно одинаковы (рис. 5.4, б). Относительное значение падения напряжения 
равно
, (5.1)
где U – номинальное или среднее напряжение ветви;
– поток активной мощности по ветви ij.
|
| Рис. 5.4. Векторная диаграмма напряжений для ветви электрической сети и её упрощения: а – общий случай; б – для системообразующей сети; в – для распределительной сети |
В первом случае параметр 
в (5.1) представляет собой угол между векторам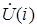и 
и 
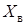, численно выраженный в радианах. Во втором случае рассматриваются распределительные сети напряжением 110 кВ и ниже, для которых и примерно равны или активное сопротивление больше реактивного. В такой сети падение напряжения в ветви равно 
(рис. 5.4, в). Относительное значение падения напряжения равно
|
|
|
. (5.2)
В (5.2) – это потери напряжения в долях номинального.
В модели постоянного тока поток активной мощности по ветви ij определяется по обобщённому выражению
, (5.3)
где 
– коэффициент для ветви ij;
– потенциал i -го узла.
Для сетей напряжением 220 кВ и более представляет собой фазовый угол вектора напряжений, а коэффициент определяется, как следует из (5.1) и (5.3), по формуле
. (5.4)
Для сетей 110 кВ и ниже потенциал - падение напряжения, а
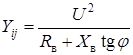. (5.5)
Коэффициенты в (5.3) – (5.5) имеют размерность мощности, а выражены в относительных единицах. Узловые потенциалы (фазы) в сети, содержащей m узлов, определяются решением линейной системы уравнений размерности (m -1)
, (5.6)
где 
– искомый вектор-столбец узловых потенциалов (или фаз потенциалов);
– квадратная матрица коэффициентов;
– вектор столбец активных нагрузок узлов сети.
Математическую модель (5.6) называют моделью постоянного тока. Эта модель может быть решена итерационными методами (методом Зейделя) или конечными методами (методом Гаусса).
|
|
|
