 |
Пример оптимизации развития электрической сети
|
|
|
|
Рассмотрим подробно процесс оптимизации развития электрической сети, показанной на рис. 5.7. Продолжительность расчётного периода – 5 лет. Изменения нагрузок узлов 1 и 2 приведены на рис. 5.8.
В течение проектного периода возможно проведение реконструкции существующей линии Л1 путем подвески второй цепи на существующие двухцепные опоры. Новые линии Л2, Л3 для присоединения новой подстанции (узла 2) - одноцепные. Коэффициент дисконтирования Е при вычислении затрат по (5.8) принят равным 0,1. Стоимость потерь электроэнергии вычисляется при 
=0,7 руб./кВт·ч.
Для описания развития сети используют вектор состояния 
, где t – номер этапа развития (t= 1, 2,…, 5). Число компонент вектора на каждом этапе равно сумме числа новых и реконструируемых линий:
.
Здесь 
– i -я компонента вектора , соответствующая i -й линии.
| 
|
| Рис.5.7. Схема, проектируемой сети | Рис. 5.8. Нагрузки сети |
В табл. 5.1 для линий Л1 – Л3 указаны по два возможных состояния (исходное - 
и конечное - 
, i =1, 2, 3), в которых может находиться каждая линия на любом этапе развития. Так как i -я линия (i= 1, 2, 3) может находиться в одном из двух состояний,
то общее число вариантов значений вектора равно
.
Таблица 5.1. – Варианты состояний линий сети
| Л1 | Л2 | Л3 | |||
| Значения компоненты вектора состояния C1 t | Характеристика состояния | Значения компоненты вектора состояния C2 t | Характеристика состояния | Значения компоненты вектора состояния C3 t | Характеристика состояния |
| Одна цепь АС-300 | Линия отсутствует | Линия отсутствует | |||
| Две цепи АС-300 | Линия АС-400 | Линия АС-300 |
Состояния сети, описываемые векторами 
и 
, недопустимы, так как в таких схемах узел 2 не имеет связей с центром питания (узлом 0), что следует из рис. 5.9.
|
|
|
Параметры, необходимые для расчётов режимов сети и экономических показателей даны в табл. 5.2. Расчёт режима (фаз потенциалов узлов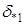 
, 
) в различных вариантах проектируемой сети (рис.5.9) осуществляется решением системы линейных уравнений (5.6). Элементы матрицы коэффициентов 
в (5.6) вычисляются по (5.4).
Рис. 5.9. Расчётные схемы сети
Таблица 5.2. – Параметры линий
| Линии | Состояние линии | |||||||||
| Исходное | Конечное | |||||||||
 ,
Ом
|  ,
Ом
|  ,
МВт
|  ,
млн. кВт·ч
|  ,
млн. руб
| , Ом
| , Ом
| ,
МВт
| ,
млн. кВт·ч
| , млн. руб
| |
| Л1 | 19,60 | 85,80 | 2,44 | - | 9,80 | 42,90 | 4,72 | 177,00 | ||
| Л2 | - | - | - | - | - | 11,25 | 63,00 | 1,37 | 281,25 | |
| Л3 | - | - | - | - | - | 9,80 | 42,90 | 1,22 | 158,00 |
Потери электроэнергии для каждого варианта развития электрической сети определены как сумма нагрузочных потерь и потерь на корону (рис.5.10).
Рис. 5.10. Суммарные потери электроэнергии по вариантам развития
электрической сети
Нагрузочные потери рассчитаны методом числа часов максимальных потерь, рассмотренным в § 3.4.
В качестве примера расчёта элементов матрицы коэффициентов рассмотрим схему проектируемой сети, соответствующую вектору состояния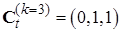 
, (см. рис. 5.9). В этом состоянии линия Л1 имеет одну цепь с проводами АС-300 (исходное состояние), линия Л2 – одна цепь с проводами АС-400 (конечное состояние) и линия Л3 – одна цепь с проводами АС-300 (конечное состояние) (см. табл. 5.1).
Коэффициенты 
для ветвей этой схемы вычислены по (5.4) при U =230 кВ:
Диагональные элементы матрицы и матрица в целом равны
(5.14)
Решение системы линейных уравнений (5.6) для рассматриваемой задачи может быть выполнено методом обратной матрицы
(5.15)
где 
, 
– нагрузки узлов 1 и 2 в году t.
Матрица обратная по отношению к матрице (5.14) определяется следующим образом.
,
где 
– алгебраическое дополнение элемента в определителе 
.
|
|
|
Определитель матрицы (5.14) равен
.
Обратная матрица
.
Искомые фазы потенциалов узлов для схемы, определяемой вектором 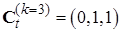, при нагрузках узлов схемы сети года t =1 вычисляются по (5.15).
.
Потоки мощности по ветвям сети (см. рис. 5.9) определяются по формуле (5.3).
МВт;
МВт;
МВт.
Расчётные потоки мощности по ветвям 
сравниваются с предельно допустимыми (см. в табл. 5.2). На основании чего делается вывод о допустимости рассматриваемого варианта схемы (вектора состояния) в году t.
Нагрузочные потери мощности в линиях в году t =1 вычислены по формуле
МВт,
а потери электроэнергии равны
Результаты расчётов режимов для вариантов схем рис. 5.9 для всех лет расчётного периода приведены в табл. 5.3.
В этой таблице режимы недопустимые по условиям ограничений на передаваемую мощность выделены курсивом. Для недопустимых режимов расчёты потерь мощности и энергии не выполняются.
Множество допустимых состояний в каждом году расчётного периода 
связаны между собой дугами графа развития сети (рис. 5.11). Допустимость переходов от одного состояния к другому 
проверяется по условию (5.7). Каждой дуге графа развития ставятся в соответствие капиталовложения в сеть, а каждой вершине – эксплуатационные затраты, включающие и приращение стоимости потерь электроэнергии. Из рис. 5.11 следует, что даже для простой схемы сети существует большое количество путей развития, начинающихся в исходном состоянии 
и заканчивающихся в одном из допустимых состояний 
. Целенаправленный поиск оптимального пути развития выполняется с использованием многошагового алгоритма метода динамического программирования, рассмотренного в § 5.3.
Таблица 5.3. – Параметры схем и режимов проектируемой сети
| k |
| Параметры схемы | Параметры режима | Годы расчётного периода | ||||
| t =1 | t =2 | t =3 | t =4 | t =5 | ||||
| (0,0,1) | Y= | P у1, МВт | ||||||
| -1849,65 | 1233,10 | P у2, МВт | ||||||
| 1233,10 | -1233,10 | δ*1, рад | -0,13 | -0,20 | -0,28 | -0,44 | -0,57 | |
| det[ Yij ]= | 760268,0924 | δ*2, рад | -0,15 | -0,24 | -0,34 | -0,54 | -0,69 | |
| P 01, МВт | 175 | - | - | |||||
| Y-1= | P 02, МВт | 0 | - | - | ||||
| -0,00162193 | -0,00162193 | P 12, МВт | - | - | ||||
| -0,00162193 | -0,00243289 | Δ P нагр, МВт | 3,966 | 9,769 | - | - | ||
| Δ W, млн. кВт·ч | 19,522 | 42,737 | - | - | - | |||
| (0,1,0) | Y= | P у1, МВт | ||||||
| -616,55 | P у2, МВт | |||||||
| -839,68 | δ*1, рад | -0,08 | -0,12 | -0,16 | -0,24 | -0,32 | ||
| det[ Yij ]= | 517706,3677 | δ*2, рад | -0,04 | -0,06 | -0,09 | -0,14 | -0,18 | |
| P 01, МВт | 200 | |||||||
| Y-1= | P 02, МВт | 150 | ||||||
| -0,00162193 | P 12, МВт | |||||||
| -0,00119093 | Δ P нагр, МВт | 1,746 | 4,087 | 7,658 | 17,811 | - | ||
| Δ W, млн. кВт·ч | 10,798 | 20,161 | 34,446 | 75,055 | - |
|
|
|
Продолжение табл. 5.3
| k |
| Параметры схемы | Параметры режима | Годы расчётного периода | ||||
| t =1 | t =2 | t =3 | t =4 | t =5 | ||||
| (0,1,1) | Y= | P у1, МВт | ||||||
| -1849,65 | 1233,10 | P у2, МВт | ||||||
| 1233,10 | -2072,78 | δ*1, рад | -0,06 | -0,09 | -0,13 | -0,20 | -0,26 | |
| det[Y]= | 2313387,196 | δ*2, рад | -0,05 | -0,08 | -0,11 | -0,18 | -0,23 | |
| P 01, МВт | 37,480 | 57,864 | 79,890 | 122,300 | 159,781 | |||
| Y-1= | P 02, МВт | 42,520 | 67,136 | 95,110 | 147,700 | 190,219 | ||
| -0,00089599 | -0,00053303 | P 12, МВт | -12,520 | -17,136 | -20,110 | -27,700 | -40,219 | |
| -0,00053303 | -0,00079954 | Δ P нагр, МВт | 1,459 | 3,521 | 6,818 | 16,130 | - | |
| Δ W, млн. кВт·ч | 10,870 | 19,117 | 32,304 | 69,553 | - | |||
| (1,0,1) | Y= | P у1, МВт | ||||||
| -2466,20 | 1233,10 | P у2, МВт | ||||||
| 1233,10 | -1233,10 | δ*1, рад | -0,06 | -0,10 | -0,14 | -0,22 | -0,28 | |
| det[Y]= | 1520536,185 | δ*2, рад | -0,09 | -0,14 | -0,20 | -0,32 | -0,41 | |
| P 01, МВт | 80,000 | 125,000 | 175,000 | 270,000 | 350,000 | |||
| Y-1 | P 02, МВт | 0 | ||||||
| -0,00081096 | -0,00081096 | P 12, МВт | 30,000 | 50,000 | 75,000 | 120,000 | 150,000 | |
| -0,00081096 | -0,00162193 | Δ P нагр, МВт | 2,113 | 5,246 | 10,493 | 25,270 | - | |
| Δ W, млн. кВт·ч | 14,392 | 26,926 | 47,912 | 107,020 | - |
Продолжение табл. 5.3
| k |
| Параметры схемы | Параметры режима | Годы расчётного периода | ||||||
| t =1 | t =2 | t =3 | t =4 | t =5 | ||||||
| (1,1,0) | Y= | P у1, МВт | ||||||||
| -1233,10 | 0,00 | P у2, МВт | ||||||||
| 0,00 | -839,68 | δ*1, рад | -0,04 | -0,06 | -0,08 | -0,12 | -0,16 | |||
| det[Y]= | 1035412,735 | δ*2, рад | -0,04 | -0,06 | -0,09 | -0,14 | -0,18 | |||
| P 01, МВт | ||||||||||
| Y-1= | P 02, МВт | |||||||||
| -0,00081096 | P 12, МВт | |||||||||
| -0,00119093 | Δ P нагр, МВт | 1,023 | 2,459 | 4,764 | 11,298 | 19,055 | ||||
| Δ W, млн. кВт·ч | 10,183 | 15,928 | 25,147 | 51,284 | 82,312 | |||||
| (1,1,1) | Y= | P у1, МВт | ||||||||
| -2466,20 | 1233,10 | P у2, МВт | ||||||||
| 1233,10 | -2072,78 | δ*1, рад | -0,04 | -0,06 | -0,08 | -0,13 | -0,17 | |||
| det[Y]= | 3591361,656 | δ*2, рад | -0,04 | -0,06 | -0,09 | -0,13 | -0,17 | |||
| P 01, МВт | 48,286 | 74,546 | 102,923 | 157,560 | 205,847 | |||||
| Y-1= | P 02, МВт | 31,714 | 50,454 | 72,077 | 112,440 | 144,153 | ||||
| -0,00057716 | -0,00034335 | P 12, МВт | -1,714 | -0,454 | 2,923 | 7,560 | 5,847 | |||
| -0,00034335 | -0,0006867 | Δ P нагр, МВт | 1,010 | 2,455 | 4,795 | 11,404 | 19,180 | |||
| Δ W, млн. кВт·ч | 11,352 | 17,131 | 26,493 | 52,927 | 84,033 | |||||
|
|
|
Рис. 5.11. Граф развития электрической сети
На первом шаге рассматриваются все возможные пути развития, от состояния до каждого допустимого состояния 
при t =1 (рис. 5.12). В каждое состояние на этом шаге ведёт только один путь (одна дуга графа) и проблемы выбора лучшего по затратам пути здесь не существует. Затраты 
на первом шаге вычисляются по (5.10). Капиталовложения первого шага и затраты на рис. 5.12 даны в млн. рублей.
На втором шаге возникает множество путей от начального состояния до каждого допустимого состояния 
в году t =2 (см. рис. 5.12). Например, в состояние 
ведут три допустимых пути: 
, 
, 
.
| 
|
| Рис. 5.12. Первый и второй шаги оптимизации развития электрической сети |
Капитальные вложения на любом шаге вычисляются следующим образом. Сравниваются значения компонент векторов состояния и вычисляются капитальные вложения с использованием данных табл. 5.2.
,
где 
– капитальные вложения в i -ю линию.
Например, для перехода 
(
) капитальные вложения равны
млн. руб.,
для перехода 
(
)
млн. руб.
Стоимость изменения потерь электроэнергии при переходе определяется с использованием результатов расчёта режимов, приведённых в табл. 5.3. Например, при переходе потери электроэнергии изменяются следующим образом.
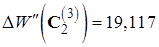млн. кВт·ч; 
млн. кВт·ч;
млн. кВт·ч.
Здесь видно сопутствующее снижение потерь электроэнергии при развитии электрической сети. Стоимость изменения потерь в этом случае равна
млн. руб.
Эксплуатационные расходы при переходе определяются стоимостью сети в состоянии 
и нормативом отчислений на обслуживание сети.
млн. руб.
Затраты при пути развития определяются по (5.11).
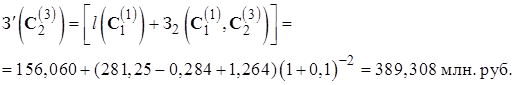
Затраты при пути развития определяются аналогично.
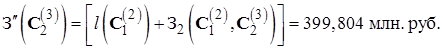
Для пути
Минимальные затраты для пути развития, заканчивающегося в состоянии 
, равны 
млн. руб.
Необходимо для каждого состояния выбрать по одному пути, которому соответствует минимум затрат (5.11). Этот путь сохраняется и называется условно-оптимальным. Остальные пути отметаются. Условно-оптимальные пути (переходы) для третьего, четвёртого и пятого шагов (рис. 5.13, 5.14, 5.15) определяются аналогично по общей формуле (5.12).
|
|
|
При выполнении пятого шага оптимизации выявлены два альтернативных пути развития электрической сети (см. рис. 5.15). Первый из них заканчивается в состоянии 
, а второй – в состоянии 
. Суммарные затраты за расчётный период в первом случае составляют 
млн. руб., а во втором – 
млн. руб. Сравнивая эти затраты, выбираем оптимальное решение для последнего года расчётного периода 
.
Рис. 5.13. Третий шаг оптимизации развития электрической сети
Рис. 5.14. Четвёртый шаг оптимизации развития электрической сети
Рис.5.15. Пятый шаг оптимизации развития электрической сети
Оптимальные состояния предыдущих лет расчётного периода определяются ходом назад, двигаясь по условно оптимальным переходам. В состояние ведёт условно оптимальный переход из состояния 
. Именно это состояние и рассматривается как оптимальное для года t =4, т.е. 
. Согласно рис. 5.14 состоянию предшествует состояние 
и т.д.
Оптимальное развитие сети показано на рис. 5.16, а расчёты затрат приведены в табл. 5.4.
Рис. 5.16. Оптимальное развитие электрической сети
Таблица 5.4. – Оптимизация развития электрической сети
| Год t | Коэф. прив. (1+ Е)- t | Вектор | Вектор | Потери энергии, млн. кВт·ч | Составляющие затрат, млн. руб. | ||||||||
| j | 
| k | 
| Δ W ” | Δ W ’ | δ W | 
| 
| 
| 
| 
| ||
| 0,909 | (0,0,0) | (0,0,1) | 19,522 | 0,000 | 19,522 | 158,000 | 13,666 | 0,000 | 156,060 | 156,060 | |||
| (0,1,0) | 10,798 | 0,000 | 10,798 | 281,250 | 7,559 | 0,000 | 262,553 | 262,553 | |||||
| (0,1,1) | 10,870 | 0,000 | 10,870 | 439,250 | 7,609 | 0,000 | 406,235 | 406,235 | |||||
| (1,0,0) | Состояние недопустимо по режиму | ||||||||||||
| (1,0,1) | 14,392 | 0,000 | 14,392 | 335,000 | 10,075 | 0,000 | 313,704 | 313,704 | |||||
| (1,1,0) | 10,183 | 0,000 | 10,183 | 458,250 | 7,128 | 0,000 | 423,071 | 423,071 | |||||
| (1,1,1) | 11,352 | 0,000 | 11,352 | 616,250 | 7,947 | 0,000 | 567,451 | 567,451 | |||||
| 0,826 | (0,0,1) | (0,0,1) | 42,737 | 19,522 | 23,215 | 0,000 | 16,250 | 1,264 | 170,534 | 170,534 | |||
| (0,1,0) | (0,1,0) | 20,161 | 10,798 | 9,363 | 0,000 | 6,554 | 2,250 | 269,829 | 269,829 | ||||
| (0,0,1) | (0,1,1) | 19,117 | 19,522 | -0,406 | 281,250 | -0,284 | 1,264 | 389,308 | 389,308 | ||||
| (0,1,0) | 10,798 | 8,319 | 158,000 | 5,823 | 2,250 | 399,804 | |||||||
| (0,1,1) | 10,870 | 8,247 | 0,000 | 5,773 | 3,514 | 413,910 | |||||||
| (0,0,1) | (1,0,1) | 26,926 | 19,522 | 7,403 | 177,000 | 5,182 | 1,264 | 307,668 | 307,668 | ||||
| (1,0,1) | 14,392 | 12,534 | 0,000 | 8,774 | 2,680 | 323,170 | |||||||
| (0,1,0) | (1,1,0) | 15,928 | 10,798 | 5,130 | 177,000 | 3,591 | 2,250 | 413,662 | 413,662 | ||||
| (1,1,0) | 10,183 | 5,745 | 0,000 | 4,021 | 3,666 | 429,424 | |||||||
| (0,0,1) | (1,1,1) | 17,131 | 19,522 | -2,392 | 458,250 | -1,674 | 1,264 | 534,440 | 534,440 | ||||
| (0,1,0) | 10,798 | 6,333 | 335,000 | 4,433 | 2,250 | 544,936 | |||||||
| (0,1,1) | 10,870 | 6,261 | 177,000 | 4,382 | 3,514 | 559,042 | |||||||
| (1,0,1) | 14,392 | 2,738 | 281,250 | 1,917 | 2,680 | 549,941 | |||||||
| (1,1,0) | 10,183 | 6,947 | 158,000 | 4,863 | 3,666 | 560,699 | |||||||
| (1,1,1) | 11,352 | 5,778 | 0,000 | 4,045 | 4,930 | 574,869 |
Продолжение табл. 5.4
| Год t | Коэф. прив. (1+ Е)- t | Вектор | Вектор | Потери энергии, млн. кВт·ч | Составляющие затрат, млн. руб. | ||||||||||
| j |
| k |
| ΔW” | ΔW’ | δW | 
|
|
|
|
| ||||
| 0,751 | (0,0,1) | (0,0,1) | Состояние недопустимо по режиму | ||||||||||||
| (0,1,0) | (0,1,0) | 34,446 | 20,161 | 14,285 | 0,000 | 9,999 | 2,250 | 279,033 | 279,033 | ||||||
| (0,0,1) | (0,1,1) | 32,304 | 42,737 | -10,433 | 281,250 | -7,303 | 1,264 | 377,304 | 377,304 | ||||||
| (0,1,0) | 20,161 | 12,143 | 158,000 | 8,500 | 2,250 | 396,614 | |||||||||
| (0,1,1) | 19,117 | 13,187 | 0,000 | 9,231 | 3,514 | 398,883 | |||||||||
| (0,0,1) | (1,0,1) | 47,912 | 42,737 | 5,175 | 177,000 | 3,622 | 1,264 | 307,188 | 307,188 | ||||||
| (1,0,1) | 26,926 | 20,986 | 0,000 | 14,690 | 2,680 | 320,719 | |||||||||
| (0,1,0) | (1,1,0) | 25,147 | 20,161 | 4,986 | 177,000 | 3,490 | 2,250 | 407,125 | 407,125 | ||||||
| (1,1,0) | 15,928 | 9,219 | 0,000 | 6,453 | 3,666 | 421,265 | |||||||||
| (0,0,1) | (1,1,1) | 26,493 | 42,737 | -16,245 | 458,250 | -11,371 | 1,264 | 507,231 | 507,231 | ||||||
| (0,1,0) | 20,161 | 6,332 | 335,000 | 4,432 | 2,250 | 526,540 | |||||||||
| (0,1,1) | 19,117 | 7,376 | 177,000 | 5,163 | 3,514 | 528,810 | |||||||||
| (1,0,1) | 26,926 | -0,433 | 281,250 | -0,303 | 2,680 | 520,761 | |||||||||
| (1,1,0) | 15,928 | 10,564 | 158,000 | 7,395 | 3,666 | 540,680 | |||||||||
| (1,1,1) | 17,131 | 9,362 | 0,000 | 6,554 | 4,930 | 543,067 | |||||||||
Продолжение табл. 5.4
| Год t | Коэф. прив. (1+ Е)- t | Вектор | Вектор | Потери энергии, млн. кВт·ч | Составляющие затрат, млн. руб. | ||||||||||
| j |
| k |
| ΔW” | ΔW’ | δW | 
|
|
|
|
| ||||
| 0,683 | (0,1,0) | (0,1,0) | 75,055 | 34,446 | 40,609 | 0,000 | 28,427 | 2,250 | 299,985 | 299,985 | |||||
| (0,1,0) | (0,1,1) | 69,553 | 34,446 | 35,107 | 158,000 | 24,575 | 2,250 | 405,271 | 397,514 | ||||||
| (0,1,1) | 32,304 | 37,249 | 0,000 | 26,075 | 3,514 | 397,514 | |||||||||
| (1,0,1) | (1,0,1) | 107,020 | 47,912 | 59,108 | 0,000 | 41,376 | 2,680 | 337,279 | 337,279 | ||||||
| (0,1,0) | (1,1,0) | 51,284 | 34,446 | 16,838 | 177,000 | 11,787 | 2,250 | 409,513 | 409,513 | ||||||
| (1,1,0) | 25,147 | 26,136 | 0,000 | 18,296 | 3,666 | 422,125 | |||||||||
| (0,1,0) | (1,1,1) | 52,927 | 34,446 | 18,481 | 335,000 | 12,936 | 2,250 | 518,215 | 503,514 | ||||||
| (0,1,1) | 32,304 | 20,623 | 177,000 | 14,436 | 3,514 | 510,458 | |||||||||
| (1,0,1) | 47,912 | 5,015 | 281,250 | 3,510 | 2,680 | 503,514 | |||||||||
| (1,1,0) | 25,147 | 27,779 | 158,000 | 19,445 | 3,666 | 530,827 | |||||||||
| (1,1,1) | 26,493 | 26,434 | 0,000 | 18,504 | 4,930 | 523,236 | |||||||||
| 0,621 | (0,1,0) | (0,1,0) | Состояние недопустимо по режиму | ||||||||||||
| (0,1,0) | (0,1,1) | Состояние недопустимо по режиму | |||||||||||||
| (0,1,1) | |||||||||||||||
| (1,0,1) | (1,0,1) | Состояние недопустимо по режиму | |||||||||||||
| (0,1,0) | (1,1,0) | 82,312 | 75,055 | 7,257 | 177,000 | 5,080 | 2,250 | 414,439 | 414,439 | ||||||
| (1,1,0) | 51,284 | 31,028 | 0,000 | 21,720 | 3,666 | 425,276 | |||||||||
| (0,1,0) | (1,1,1) | 84,033 | 75,055 | 8,978 | 335,000 | 6,285 | 2,250 | 513,293 | 503,586 | ||||||
| (0,1,1) | 69,553 | 14,480 | 177,000 | 10,136 | 3,514 | 523,649 | |||||||||
| (1,0,1) | 107,020 | -22,986 | 281,250 | -16,090 | 2,680 | 503,586 | |||||||||
| (1,1,0) | 51,284 | 32,750 | 158,000 | 22,925 | 3,666 | 524,129 | |||||||||
| (1,1,1) | 52,927 | 31,107 | 0,000 | 21,775 | 4,930 | 534,796 | |||||||||
В табл. 5.4 полужирным шрифтом выделены векторы состояния 
и составляющие затрат, входящие в условно оптимальные пути. Величины Δ W ” в табл. 5.4 – это потери электроэнергии в схеме сети, определяемой вектором 
, а Δ W ’ – потери электроэнергии в сети, представленной вектором . Величины δ W – приращение потерь электроэнергии при переходе от состояния к состоянию .
Из рис. 5.16 и табл. 5.4 видно, что в оптимальном варианте развития сети капиталовложения сдвигаются на возможно более поздний шаг расчётного периода. Изменения в сети диктуются появлением нового узла и необходимой разгрузкой линий рассматриваемой сети.
|
|
|
