 |
Развития электрической сети
|
|
|
|
Развитие электрической сети и ЭЭС в целом представляет бесконечный последовательный процесс смены состояний сети при росте нагрузок существующих узлов, появлении новых нагрузок, замене изношенного оборудования. Под состоянием сети понимается фиксированный для некоторого момента времени состав параметров оборудования и режимов. Практически возможно рассмотреть развитие сети в ограниченном расчётном периоде времени T р. Состояние сети в удобно описывать с помощью вектора состояния 
, где t – номер этапа развития (t= 1, 2, T р). Число компонент вектора на каждом этапе равно сумме числа новых и реконструируемых элементов сети:
.
Здесь 
– i -я компонента вектора , соответствующая i -й ветви (группе ветвей).
Для примера схемы сети, изображённой на рис. 5.5, число компонент вектора состояния m =3, а каждая из ветвей (i= 1, 2, 3) может находиться в одном из двух состояний
В примере рис. 5.5 решается задача выбора оптимальной схемы присоединения к сети новой подстанции «п/ст 2» линиями «Л 2», «Л 3» и увеличения пропускной способности существующей линии «Л 1» при подвеске второй цепи. Число вариантов значений вектора равно
.
Используя векторы состояния, многовариантное развитие электрической сети (рис. 5.5) можно представить в виде направленного графа (рис. 5.6).
|
Вершинами графа развития являются различные варианты вектора состояния 
(k =0, 1,..., N -1) в момент времени t. Дуги графа отражают возможности перехода из одного состояния в другое 
(j, k =0, 1,..., N -1), им соответствуют определённые затраты (капитальные и эксплуатационные) необходимые для такого перехода. Существует множество допустимых дуг (путей), соединяющих начальную вершину 
с одной из вершин 
(k =0, 1,..., N -1), находящейся на уровне t = T р. Допустимость путей и состояний (вершин графа) проверяется сопоставлением расчётных величин потоков мощности и напряжений с предельно возможными для рассматриваемого состояния сети. Переход из одного состояния в другое возможен, если возможен переход по каждой компоненте вектора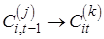 
. Для этого должно выполняться условие
|
|
|
(j, k =0, 1,..., N -1). (5.7)
Рис. 5.6. Граф развития электрической сети
Среди допустимых путей от до (k =0, 1,..., N -1) и необходимо найти путь «кратчайшей длины», для которого суммарные дисконтированные затраты на последовательные переходы от одного состояния к другому – минимальны
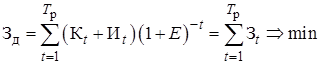, (5.8)
где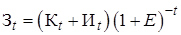 
– затраты в году t с учётом их дисконтирования.
Капитальные вложения 
определяются изменениями сети в году t при переходе , т.е. зависят от 
, и 
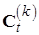. Эксплуатационные затраты 
состоят из суммы расходов на обслуживание, ремонт Иобс t и стоимости изменения потерь электроэнергии при вводе новых объектов 
, определяемой по средневзвешенному тарифу на электроэнергию 
. Величина Иобс t зависит от всех капиталовложений, осуществлённых за период от первого года до года (t -1), и определяется значением вектора состояний . Изменения потерь электроэнергии 
зависят от состояний 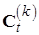, , нагрузок года t и (t -1).
Таким образом для всего расчётного периода затраты (5.8) равны сумме затрат для каждого перехода в отдельности, т.е. обладают свойствами аддитивности:
. (5.9)
Целенаправленный поиск оптимального пути развития сети из множества возможных S с использованием графа развития выполняется методом динамического программирования, основанного на принципе оптимальности [16, 17]. Согласно этому принципу любой участок оптимального пути является оптимальным. Метод динамического программирования применительно к задаче поиска минимума (5.9) позволяет на каждом шаге t решать задачу минимизации только по переменным и последовательно уменьшать число конкурентноспособных вариантов из множества S.
|
|
|
Алгоритм решения представляет собой многошаговый процесс, на каждом шаге которого производят «отметание» некоторого множества вариантов St, о котором в процессе работы алгоритма становится известным, что оно не содержит участка оптимального пути.
Обозначим через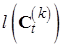 
минимальные затраты на переход от вершины 
до вершины 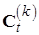. На первом шаге
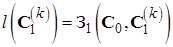(5.10)
и сужения множества S не происходит. На втором шаге рассмотрим пути от вершины до любой вершины 
. Путь с минимальными затратами определим из соотношения
. (5.11)
Любой путь, проходящий через 
и не содержащий участка 
, не может быть претендентом на оптимальность. Множество вариантов S 2, которое мы исключаем на этом шаге, состоит из всех путей, не содержащих участка .
Пусть теперь для каждой вершины определены затраты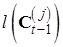 
на пути от исходной вершины . Тогда минимальные затраты на пути, соединяющим любую вершину 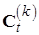и , равны
. (5.12)
Все варианты путей St, не содержащие участка 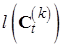, отбрасываются. Формула (5.12) – это общее рекуррентное уравнение, описывающее многошаговый процесс отыскания решения. Продолжая расчёт по (5.10) на последнем шаге (t = T р) получим для каждой вершины 
значение функции 
. Чтобы завершить процедуру поиска оптимального пути, выполним ещё одну процедуру минимизации:
. (5.13)
Применение метода динамического программирования для решения модели оптимизации развития электрической сети позволяет учесть нелинейность технико-экономических показателей, дискретное изменение параметров, динамизм развития. Однако реализация данного метода предъявляет высокие требования к объёму памяти и быстродействию ЭВМ. Уменьшение числа рассматриваемых состояний может быть достигнуто предварительным анализом условий развития сети, выполненным проектировщиком.
|
|
|
