 |
Последовательность расчета
|
|
|
|
Краматорск 2012
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ, МОЛОДЕЖИ
И СПОРТА УКРАИНЫ
ДОНБАССКАЯ ГОСУДАРСТВЕННАЯ МАШИНОСТРОИТЕЛЬНАЯ АКАДЕМИЯ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторным, контрольным и самостоятельным работам
по дисциплине
«Автоматизированное проектирование оптимальных конструкций»
для студентов очной и заочной форм обучения
специальности 7, 8.050102
| Переутверждено на заседании методического совета |
| Протокол №6 от 20.02.2012 |
Краматорск 2012
УДК 004:621.001.2
Методические указания к лабораторным, контрольным и самостоятельным работам по дисциплине «Автоматизированное проектирование оптимальных конструкций» для студентов очной и заочной форм обучения специальности 7, 8.050102/ Сост. С.А. Короткий, Ю.А. Шабалина, С.В. Таран. – Краматорск: ДГМА, 2012. – 72 с.
Составители: С.А. Короткий, ст. преп.,
Ю.А. Шабалина, ассист.,
С.В. Таран, ассист.
Ответственный А.Ф. Тарасов, проф.
за выпуск
СОДЕРЖАНИЕ
1 Статический анализ конструкций...................................... 4
1.1 Постановка задачи линейного статического анализа.................... 4
1.2 Выполнение статического анализа конструкции в COSMOSWorks.. 8
1.3 Выполнение статического анализа конструкции в среде ABAQUS 20
1.4 Лабораторная работа 1. Статический анализ детали в среде CAE-системы COSMOSWorks............................................................................................. 25
1.5 Лабораторная работа 2. Статический анализ детали в среде CAE-системы ABAQUS........................................................................................................ 40
1.6 Контрольные вопросы................................................................... 41
2 Частотный анализ конструкций........................................ 42
2.1 Постановка задачи частотного анализа........................................ 42
|
|
|
2.2 Выполнение частотного анализа в COSMOSWorks.................... 43
2.3 Лабораторная работа 3. Выполнение частотного анализа конструкции в среде САЕ-системы COSMOSWorks............................................................ 46
2.4 Контрольные вопросы................................................................... 46
3 Анализ критических нагрузок и форм потери устойчивости конструкций.............................................................. 47
3.1 Постановка задачи анализа........................................................... 47
3.2 Выполнение анализа устойчивости в COSMOSWorks................ 48
3.3 Лабораторная работа 4. Анализ устойчивости конструкции в среде САЕ-системы COSMOSWorks............................................................................... 51
3.4 Контрольные вопросы................................................................... 51
4 Тепловой расчет конструкций............................................ 52
4.1 Постановка задачи анализа........................................................... 52
4.2 Выполнение теплового анализа в COSMOSWorks...................... 53
4.3 Лабораторная работа 5. Выполнение теплового анализа конструкции в среде САЕ-системы COSMOSWorks............................................................ 57
4.4 Контрольные вопросы................................................................... 63
5 Оптимизация конструкций................................................... 64
5.1 Постановка задачи анализа........................................................... 64
5.2 Выполнение оптимизационного расчета в COSMOSWorks........ 65
5.3 Лабораторная работа 6. Выполнение оптимизации конструкции в среде CAE-системы COSMOSWorks...................................................................... 69
5.4 Контрольные вопросы................................................................... 70
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ................................... 71
1 Статический анализ конструкций
1.1 Постановка задачи линейного статического анализа
Если динамические эффекты в исследуемой системе пренебрежимо малы по причине того, что приложенные нагрузки являются квазистатическими, то такую задачу можно отнести к классу статических задач.
Если отношение между приложенной силой и полученными деформациями изменяется по линейному закону, то задача относится к классу задач линейного статического анализа (рисунок 1.1).
|
|
|
Рисунок 1.1 – Зависимости между силой и перемещением при линейном и нелинейном статических анализах
Линейный статический анализ преимущественно связан с вычислением перемещений, относительных деформаций и напряжений, возникающих под действием статических внешних сил.
При проведении линейного статического анализа возможны ситуации, когда под действием внешних сил, приложенных к конструкции, наступает ее разрушение или пластическое деформирование. Для оценки этих явлений используются так называемые критерии прочности, которые позволяют предсказать различные случаи разрушения конструкции. Выявление таких случаев требует обширных знаний о поведении конструкции под действием внешних нагрузок. Как правило, в качестве критерия прочности используются критерии, основанные на анализе величины напряжения текучести материала. При этом определяется отношение напряжения текучести материала к максимальному напряжению в конструкции, возникающему под действием внешних нагрузок.
Как правило, используются следующие критерии прочности материалов:
- критерий максимальных эквивалентных напряжений сдвига по Мизесу;
- критерий максимальных касательных напряжений (критерий Треска);
- критерий Мора-Кулона;
- критерий максимальных нормальных напряжений.
Критерий Мизеса определяет момент исчерпания несущей способности конструкции путем сравнения величины эквивалентного напряжения с пределом текучести материала. Эквивалентное напряжение 
в некоторой точке твердого тела рассчитывается по формуле
где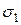 
, 
, 
– главные напряжения.
Критерий Мизеса применим для изотропных материалов, имеющих вязкий характер разрушения. К ним относят большинство металлов, а также некоторые пластмассы, демонстрирующие помимо вязкого разрушения линейный участок на диаграмме деформирования.
В пространстве поверхность прочности по критерию Мизеса описывается прямым круговым цилиндром, ось которого совпадает с пространственной диагональю, проходящей в положительном октанте системы координат главных напряжений. Сечением поверхности прочности любой из плоскостей, соответствующих нулевому значению одного из главных напряжений, является эллипс, проходящий через точки – пределы прочности материала 
(рисунок 1.2).
|
|
|
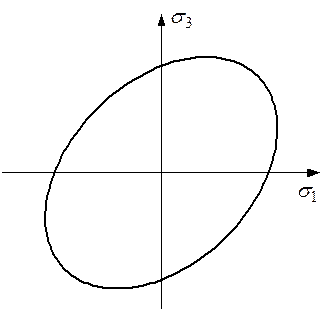
Рисунок 1.2 – Эллипс Мизеса
Коэффициент запаса прочности конструкции 
вычисляется как отношение величины прочности (предела текучести, предела прочности и т.д.) к максимальному в объеме детали эквивалентному напряжению:
.
Критерий максимальных касательных напряжений заключается в сравнении величины максимального касательного напряжения в некоторой точке детали 
относительно некоторой предельной величины напряжений, задаваемой пользователем.
Поверхность прочности для этого критерия представляет собой прямую правильную шестигранную призму, ось которой совпадает с диагональю положительного октанта системы координат главных напряжений. Сечение поверхности прочности плоскостью 
представляет собой шестиугольник, вписанный в эллипс Мизеса (рисунок 1.3).
Рисунок 1.3 – Критерий максимальных касательных напряжений для плоского напряженного состояния
Коэффициент запаса прочности при использовании критерия Треска определяется как отношение величины прочности (предела текучести, предела прочности и т.д.) к удвоенному (в силу парности касательных напряжений) максимальному в объеме детали касательному напряжению:
.
Критерий Мора-Кулона (критерий внутреннего трения) используется для хрупких материалов, которые по-разному сопротивляются растяжению и сжатию (рисунок 1.4).
Рисунок 1.4 – Критерий Мора-Кулона для плоского напряженного состояния
Коэффициент запаса прочности при использовании критерия Мора-Кулона зависит от первого и третьего главных напряжений , :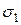
Критерий максимальных нормальных напряжений используется для хрупких материалов, которые одинаково сопротивляются растяжению и сжатию. В связи с тем, что это условие редко соблюдается на практике (например, вследствие того, что дефекты в виде трещин при растяжении ослабляют хрупкие материалы гораздо существеннее, чем при сжатии), этот критерий необходимо использовать с максимальной осторожностью.
|
|
|
Поверхность прочности представляет собой куб, грани которого перпендикулярны осям главных напряжений. Сечение поверхности плоскостью с нулевым главным напряжением представляет собой квадрат (рисунок 1.5).
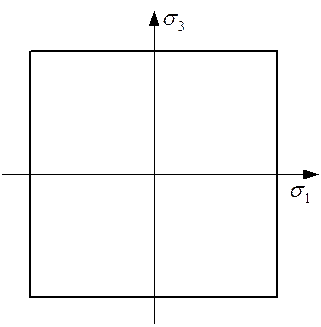
Рисунок 1.5 – Критерий максимальных нормальных напряжений
Коэффициент запаса прочности при использовании критерия максимальных нормальных напряжений зависит от первого главного напряжения :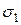
.
1.2 Выполнение статического анализа конструкции в COSMOSWorks
Интерфейс COSMOSWorks
COSMOSWorks имеет стандартный интерфейс приложения SolidWorks. После активизации COSMOSWorks с использованием команды «Инструменты à Добавления» в меню SolidWorks возникает соответствующий пункт, который объединяет функциональные возможности COSMOSWorks. Справа в окне SolidWorks появляется менеджер COSMOSWorks, представляющий собой дерево. В нем отображаются позиции, характеризующие проект в целом (пиктограмма с названием детали или сборки и пиктограмма «Параметры»), а также пиктограммы с Упражнениями, появляющиеся после их создания пользователем. Упражнения являются ветвями, объединяющими информацию о некотором расчете: материалы, сетка, граничные условия, результаты, отчеты. Каждой пиктограмме соответствует контекстное меню, содержимое которого изменяется в зависимости от текущего состояния расчетной модели.
При проведении анализа пользователь имеет возможность использовать представленные в среде COSMOSWorks пиктографические меню, которые объединяют типовые команды, используемые в процессе решения задачи.
Для решения статических задач пользователь может использовать четыре пиктографических меню:
- панель «Основные функции»;
- панель «Нагрузки»;
- панель «Показатели»;
- панель «Инструменты результатов».
Общий вид перечисленных кнопочных панелей приведен на
рисунках 1.6-1.9, а описание функционального назначения вынесенных на панели кнопок – в таблицах 1.1-1.4.
Рисунок 1.6 – Панель «Основные функции»
Таблица 1.1 – Назначение кнопок панели «Основные функции»
| Пиктограмма | Наименование | Назначение | |
| Англоязычная версия | Русскоязычная версия | ||
| Study | Упражнение | Создание нового упражнения, изменение параметров или удаление имеющегося упражнения |
| Apply material to all | Применить материал ко всем | Назначение материала или изменение характеристик уже назначенного для всех элементов папок «Твёрдотельные» («Solids») или «Оболочки» («Shells») |
| Mesh | Сетка | Конечно-элементное разбиение модели применительно к активному упражнению (Study). Перед построением сетки рекомендуется проверить действующие настройки сетки (Mesh preferences), элементы управления сеткой (Mesh control), контактные условия между деталями в сборке (Contact conditions) |
Продолжение таблицы 1.1
|
|
|
| Пиктограмма | Наименование | Назначение | |
| Англоязычная версия | Русскоязычная версия | ||
| Run | Выполнить | Расчет для активного упражнения |
| Shell using surfaces | Оболочка | Построение сетки на базе выделенных граней или поверхностей. Допускается иметь в списке выбора оба типа объектов, однако сетка будет несшитой |
| Apply mesh control | Применить элемент управления | Назначение для элементов детали или сборки параметров плотности сетки, связанных с вершинами, кромками, гранями или деталями (в случае анализа сборки). В сборке плотность можно назначать изолированно для детали или привязывать ее к плотности, которую программа использовала бы для изолированной детали. Управление плотностью в зависимости от направления не допускается |
| Set global contact | Установить глобальный контакт | Назначение контактных граничных условий по умолчанию. Допускаются совместное перемещение, независимое перемещение и контакт в исходном состоянии с возможностью отрыва. Последний тип граничных условий следует использовать, если детали могут проскальзывать. Команда доступна только при статическом анализе сборок |
Продолжение таблицы 1.1
| Пиктограмма | Наименование | Назначение | |
| Англоязычная версия | Русскоязычная версия | ||
| Define a contact set | Определить набор соприкасания | Назначение для пар взаимодействующих объектов или выделенных деталей контактных граничных условий, которые отличны от принятых по умолчанию. В дополнение к глобальным граничным условиям можно для пар граней назначать условие вхождения в контакт |
| Drop test setup | Настройка испытания на ударную нагрузку | Назначение параметров моделирования процесса падения. Допускается выбор высоты падения или скорости. Назначается ориентация плоскости, на которую падает объект и коэффициент трения. Полупространство, на которое падает модель, считается абсолютно жестким. Анализ сопровождается решением контактной задачи с переменной областью контакта |
| Result options | Параметры результатов | Настройка параметров отображения результатов выбранного упражнения. Команда доступна только после расчета |
Рисунок 1.7 – Панель «Нагрузки»
Таблица 1.2 – Назначение кнопок панели «Нагрузки»
| Пиктограмма | Наименование | Назначение | |
| Англоязычная версия | Русскоязычная версия | ||
| Restraints | Ограничения | Назначение граничных условий для выбранных элементов модели в активном механическом упражнении |
| Pressure | Сжатие | Приложение давления к выбранным граням для активного механического упражнения |
| Force | Сила | Приложение силы, крутящего или изгибающего моментов к выбранным элементам модели в активном механическом упражнении. Заданное усилие прикладывается к каждому из выбранных объектов |
| Gravity | Сила тяжести | Приложение гравитационных (или инерционных) нагрузок в активном механическом упражнении |
| Centrifugal force | Центробежная сила | Приложение центробежной силы в активном механическом упражнении |
| Remote load | Дистанционная нагрузка | Приложение удаленных нагрузок в активном механическом упражнении |
Продолжение таблицы 1.2
| Пиктограмма | Наименование | Назначение | |
| Англоязычная версия | Русскоязычная версия | ||
| Connectors | Жесткая связь | Ввод виртуальных объектов, имитирующих соединительные элементы: - «Точно»(Rigid) – включение абсолютно жесткого тела, соединяющего грани двух деталей; - «Пружина»(Spring) – включение распределенной пружины растяжения-сжатия или сдвига между плоскими гранями двух деталей; - «Шпилька»(Pin) – включение абсолютно жесткого штифта, соединяющего концентрические цилиндрические отверстия двух деталей. Штифт обеспечивает поворот или осевое смещение деталей с назначенной жесткостью; - «Поддержка упругости» (Elastic support) – имитация податливого основания, ограничивающего подвижность граней детали или деталей в сборке; - «Болт» (Bolt) – включение податливого объекта, воспроизводящего действие болта с предварительной затяжкой, которая задается осевой силой или крутящим моментом |
Продолжение таблицы 1.2
| Пиктограмма | Наименование | Назначение | |
| Англоязычная версия | Русскоязычная версия | ||
| Bearing load | Контактная сила | Приложение контактных опорных нагрузок к выбранным граням в активном механическом упражнении |
| Temperature | Температура | Назначение температуры для выбранных объектов в активном упражнении |
Рисунок 1.8 – Панель «Показатели»
Таблица 1.3 – Назначение кнопок панели «Показатели»
| Пиктограмма | Наименование | Назначение | |
| Англоязычная версия | Русскоязычная версия | ||
| Reaction force | Сила реакции | Вывод интегральной величины усилия, приложенного к некоторому геометрическому элементу детали, к детали в сборке или к сборке в целом |
| Contact force | Контактная сила | Вывод численных характеристик контактного усилия между деталями в сборке на поверхности соприкосновения |
| Pin/Bolt force | Сила шпильки/болта | Вывод осевого и сдвигового компонентов усилия, возникающего в болтовом соединении, а также крутящего момента. Компоненты, вызванные предварительным натягом, также включаются в отображаемые значения |
Продолжение таблицы 1.3
| Пиктограмма | Наименование | Назначение | |
| Англоязычная версия | Русскоязычная версия | ||
| List modes | Режимы | Отображение величин собственных частот для расчета на резонанс |
| Response graph | График ответа | Формирование кривой отклика в нелинейной задаче |
| Time history graph | Интерфейс ударной нагрузки | Определение графиков зависимости параметров в узле сетки конечных элементов от времени расчета ударной нагрузки |
Рисунок 1.9 – Панель «Инструменты результатов»
Таблица 1.4 – Назначение кнопок панели «Инструменты результатов»
| Пиктограмма | Наименование | Назначение | |
| Англоязычная версия | Русскоязычная версия | ||
| Design check wizard | Проверка прочности | Активизация помощника проверки проектирования для активного статического упражнения, который осуществляет сравнение результатов расчета напряжений с выбранным критерием прочности |
| Stress | Напряжение | Визуализация диаграмм напряжений: компонентов относительно глобальной или локальной системы координат, эквивалентных напряжений по Мизесу, а также оценки ошибки вычисления напряжений |
Продолжение таблицы 1.4
| Пиктограмма | Наименование | Назначение | |
| Англоязычная версия | Русскоязычная версия | ||
| Displacement | Перемещение | Визуализация диаграмм перемещений относительно глобальной или локальной системы координат, силы реакции и ее компонентов |
| Strain | Деформация | Визуализация диаграмм деформации относительно глобальной или локальной системы координат, эквивалентных деформаций, а также плотности энергии деформирования |
| Thermal | Термическая | Визуализация диаграмм температур, градиентов температуры относительно глобальной или локальной системы координат, теплового потока и его градиентов |
| Report | Отчет | Генерация отчета, содержащего результаты текущего активного упражнения |
| Animate | Анимировать | Анимация отображаемой диаграммы |
| Clipping | Ограничение | Активизация окна «Отсечение», которое предназначено для управления сечениями активного вида или построения изоповерхностей |
| Color map | Отображение цвета | Активизация меню «Карта цветов», которое предназначено для определения цветовой палитры активной диаграммы |
Продолжение таблицы 1.4
| Пиктограмма | Наименование | Назначение | |
| Англоязычная версия | Русскоязычная версия | ||
| Settings | Параметры | Настройка параметров отображения диаграммы: способа визуализации сетки или границ деталей в модели, масштаба деформированного вида и т.д. |
| Probe | Зондирование | Вывод числового значения отображаемого результата в месте, указанном щелчком мыши на поверхности модели или в сечении. Отображается величина результата в ближайшем к указанной точке узле |
| List selected | Выбранный список | Вывод числовых значений отображаемого результата в узлах, принадлежащих заданным элементам модели. Возможно отображение графика, где абсциссой являются указанные точки |
| Save as | Сохранить как | Запись активной диаграммы в файл |
| Show/Hide mesh | Отобразить / Скрыть сетку | Отображение сетки конечных элементов. Если визуализируются какие-либо результаты, то нажатие этой кнопки приведет к отображению модели SolidWorks |
Последовательность расчета
Применение COSMOSWorks требует соблюдения базовой канвы алгоритма метода конечных элементов, предоставляя пользователю внутри каждого этапа определенную свободу в последовательности шагов подготовки модели и рассмотрения результатов. Педполагаемая цепочка событий для выполнения статического расчета в упругой постановке описана ниже.
1 Создание упражнения определенного типа и определение его настроек. Последние могут быть изменены в любой момент перед выполнением расчета.
2 Заполнение, если необходимо, таблицы параметров, определяющей набор величин, которые могут изменяться в ходе расчета.
3 Подготовка исходных данных внутри заданного анализа:
- назначение материала детали или деталей;
- назначение кинематических граничных условий;
- назначение статических граничных условий;
- создание сетки.
4 Связывание, в случае необходимости, параметров из таблицы параметров с соответствующими параметрами анализа.
5 Выполнение расчета.
6 Обработка результатов:
- создание необходимых диаграмм;
- анализ диаграмм;
- экспорт результатов.
Моделирование статической пространственной задачи теории упругости в COSMOSWorks по отношению к сопоставимым программным продуктам реализуется традиционно. Аппроксимация геометрии модели производится тетраэдральными изопараметрическими конечными элементами с линейным полем перемещений (деформации постоянные, грани плоские) и с параболическим полем перемещений (деформации линейные, грани – полиномы второго порядка).
Для расчета деталей в твердотельном представлении можно предложить рекомендации, преследующие две цели:
- повышение точности расчета;
- сокращение размерности задачи.
Во многих случаях эти две цели не являются взаимоисключающими.
Рекомендуемые методы контроля и повышения точности:
- перед решением задачи с реальной геометрией и нагрузками решить аналогичную задачу в канонической постановке (например, нагруженная балка, цилиндр под давлением и т.д.); проанализировать корреляцию между аналитическим и численным решением и сделать выводы о природе полученных различий, которые могут являться следствием ограничений используемых методов решения, невозможности корректной аппроксимации граничных условий, грубо построенной сетки конечных элементов;
- максимально использовать свойства симметрии задачи: как геометрии, так и граничных условий;
- провести расчет без учета геометрической симметрии, проверяя совпадение с расчетом при ее использовании;
- исключить особенности, порождаемые геометрией и граничными условиями (например, внутренние углы, наличие в модели элементов со значительно отличающимися геометрическими размерами и т.д.);
- провести расчет с различной плотностью сетки;
- не накладывать сразу весь комплекс нагрузок – в тестовых расчетах накладывать только простейшие нагрузки, добиваясь при этом предсказуемой реакции модели;
- для расчетов, по результатам которых будет выполнен анализ и сделаны заключения о работоспособности конструкции, использовать только параболические конечные элементы;
- не стремиться к идеальной аппроксимации криволинейной геометрии; точность геометрии не оказывает решающего влияния на точность решения; качество сетки, под которым подразумевается близость конечных элементов к правильным тетраэдрам с минимальной кривизной ребер и граней, предпочтительнее точного моделирования кривизны граней и ребер.
|
|
|
