Обязательный набор исходных данных для анализа устойчивости конструкции

 

Минимально необходимой информацией для выполнения анализа устойчивости конструкции является ее пространственная модель. Кроме этого пользователю необходимо определить тот же набор параметров, что и для статического анализа (см. п. 1.2.3). В качестве нагрузок могут выступать как усилия, так и перемещения и углы поворота. Степени свободы конструкции желательно зафиксировать таким образом, чтобы исключить ее движение как жесткого целого. Несмотря на то, что среди параметров настройки (см. рисунок 3.1) доступна опция «Использовать незакаленную пружину для стабилизации модели», использовать ее без явных причин не следует, т.к. это нарушает адекватность модели.

 

Характерные ошибки

 

Возможность сделать серьезную ошибку при выполнении анализа устойчивости конструкции достаточно невелика, т.к. наглядная визуализация форм потери устойчивости дает адекватное представление о том, насколько правильно поставлена задача.

Одним из случаев, когда может появиться ошибка, является расчет сборок с кинематически подвижными элементами. Вычислительный процесс может оказаться расходящимся вследствие некорректных контактных условий между деталями. Поэтому необходимо особенно тщательно подходить к определению контактных взаимодействий между элементами сборок. При этом доступны такие условия контакта, как совместное перемещение на границе контактируемых деталей и независимое деформирование.

В деталях из поверхностей ошибки могут порождаться несвязностью конечно-элементной аппроксимации, что является следствием некорректного построения твердотельной модели детали (наличие несшитых поверхностей).

 

Состав результатов

 

После выполнения расчетов в менеджере COSMOSWorks создаются две папки: «Перемещение» и «Деформация».

Папка «Перемещение» содержит информацию о деформированном состоянии конструкции с цветовым выделением перемещений UX, UY, UZ в направлении соответствующих осей глобальной системы координат и результирующего перемещения URES. При этом следует отметить, что абсолютные значения перемещений элементов конструкции не имеют физического смысла, т.к. функциональность программы ограничена только установлением момента потери устойчивости и соответствующей ему формы.

Папка «Деформация» содержит графические представления анализируемой конструкции, которые отображают формы потерявшей устойчивость конструкции.

 

3.3 Лабораторная работа 4. Анализ устойчивости конструкции в среде САЕ-системы COSMOSWorks

 

Используя трехмерную модель детали, построенную в лабораторной работе 1 (см. таблицу 1.5), выполнить анализ ее устойчивости в среде
САЕ-системы COSMOSWorks. Проанализировать полученные результаты расчетов, сделать выводы, которые отразить в отчете.

При оформлении отчета привести формы потери устойчивости, номера которых приведены в индивидуальном задании (таблица 3.1).

 

Таблица 3.1 – Индивидуальные задания к лабораторной работе 4

Номер варианта	Номера форм потери устойчивости	Номер варианта	Номера форм потери устойчивости
	1, 7, 15		4, 12, 18
	2, 8, 16		5, 13, 19
	3, 9, 17		6, 14, 20
	4, 10, 18		6, 15, 17
	5, 11, 19		5, 6, 18
	6, 12, 20		4, 7, 9
	6, 13, 15		3, 5, 6
	5, 14, 16		2, 7, 11
	4, 6, 17		1, 3, 18
	3, 7, 18		1, 2, 15
	2, 8, 19		2, 4, 6
	1, 8, 20		3, 10, 12
	1, 9, 15		4, 12, 15
	2, 10, 16		5, 17, 20
	3, 11, 17		6, 15, 19

 

3.4 Контрольные вопросы

 

1 Поясните явление потери устойчивости.

2 Охарактеризуйте причины возникновения потери устойчивости.

3 Поясните физический смысл коэффициента потери устойчивости.

4 Поясните понятие критической силы.

5 Объясните математические основы задачи потери устойчивости.

6 Охарактеризуйте параметры, которые используются при решении задачи потери устойчивости.

7 Поясните особенности анализа устойчивости при расчете сборок.

8 Объясните особенности разработки конечно-элементной аппроксимации конструкции при анализе устойчивости конструкции.

 

4 Тепловой расчет конструкций

4.1 Постановка задачи анализа

 

Тепловой расчет предназначен для моделирования эффектов теплопередачи внутри деталей, сборок, а также между конструкцией и окружающей средой. При разности температур контактирующих тел происходит перетекание тепловой энергии от тел с большей температурой к менее нагретым телам, а внутри детали – от более нагретых ее областей к менее нагретым. Известны три механизма теплопередачи: теплопроводность, конвекция и излучение.

Теплопроводность – это передача энергии в пределах объема однородного тела или между телами, контактирующими без зазоров. Тепловой поток , проходящий через поверхность площади при разности температур 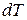на толщине ( – температурный градиент), вычисляется по формуле

 

,

 

где k – коэффициент теплопроводности, .

Идеальная модель теплопроводности подразумевает, что обмен энергией осуществляется путем взаимодействия атомов и молекул неподвижного вещества.

Конвекция – это передача энергии от поверхности тела в окружающую среду (жидкую или газообразную) за счет движения молекул газа или жидкости. Это движение может происходить по различным причинам. Если оно возникает из-за разницы в плотности, проявляющейся вследствие нагрева или охлаждения теплоносителя рассматриваемым телом, то конвекция считается естественной. Если источник движения молекул является внешним по отношению к рассматриваемой системе (например, вентилятор или насос), то конвекция классифицируется как вынужденная.

Тепловой поток между поверхностью тела, температура которой 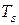, и теплоносителем с температурой через площадь рассчитывается по формуле

 

,

 

где h – коэффициент теплоотдачи, .

Излучение – это обмен энергией между телами посредством электромагнитных волн. При этом не требуется промежуточной среды (теплоносителя), а передача энергии возможна, кроме прочего, в вакууме. Если температура поверхности 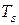, а окружающей среды , то поверхность площадью принимает тепловой поток, который можно определить по формуле

 

,

 

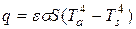где – константа Стефана-Больцмана;

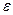– излучательная способность поверхности.

Под излучательной способностью поверхности понимают долю теплового потока поверхности относительно поверхности абсолютно черного тела, для которого .

На практике ни один из перечисленных механизмов передачи тепла в изолированном виде не существует. Однако вычислительный процесс требует выделения тех, которые определяют тепловое состояние. Внутри деталей и при их контакте доминирующую роль играет теплопроводность. Если присутствует вынужденная конвекция, то она вносит существенный вклад в распределение температур внутри модели. Излучение становится значимым при большой разнице температур тел.

Тепловой анализ может быть стационарным и нестационарным. Первый вариант заключается в поиске распределения температуры в равновесном состоянии; второй – в моделировании распространения тепла за счет теплопроводности внутри деталей и между контактирующими деталями в сборке при учете взаимодействия с окружающей средой во времени.

 

4.2 Выполнение теплового анализа в COSMOSWorks

Интерфейс COSMOSWorks

 

При выполнении теплового анализа пользователю предоставляется возможность использовать пиктографическую панель «Термические нагрузки» (рисунок 4.1), которая объединяет средства, предназначенные для описания тепловых процессов в модели. Функциональное назначение вынесенных на панель кнопок приведено в таблице 4.1.

 

 

Рисунок 4.1 – Панель «Термические нагрузки»

 

Стационарный тепловой расчет предполагает анализ распределения температур в конструкции, находящейся в состоянии теплового равновесия. При постановке задачи теплового анализа необходимо контролировать граничные условия, а для сборок – также контактные граничные условия, чтобы тепловое равновесие достигалось в принципе. Что касается сборок, это требование актуально для каждой детали.

Таблица 4.1 – Назначение кнопок панели «Термические нагрузки»

Пиктограмма	Наименование	Назначение
Англоязычная версия	Русскоязычная версия
	Temperature	Температура	Назначение температуры для выбранных объектов в активном упражнении
	Convection	Конвекция	Приложение конвекции к выбранным граням в активном упражнении
	Heat flux	Тепловой поток	Приложение теплового потока к выбранным граням в активном упражнении
	Heat power	Тепловая мощность	Приложение тепловой мощности к выбранным граням в активном упражнении. Эта величина назначается для каждой из выбранных граней
	Radiation	Излучение	Назначение параметров излучения для выбранных граней в активном упражнении

 

Параметры настройки задачи теплового анализа приведены на рисунке 4.2.

Нестационарный тепловой расчет моделирует распространение тепловой энергии в зависимости от времени. При этом граничные условия остаются неизменными. Это не значит, что величина излучаемой (принимаемой) энергии является постоянной. Она зависит от температуры поверхности самого тела, но не учитывает изменений состояния окружающей среды, происходящих в результате обмена энергией с телом.

Ниже перечислены обязательные настройки, требуемые для нестационарной задачи:

- Общее время – время, в течение которого анализируется тепловое состояние. Программа не контролирует факт сходимости расчета к стационарному состоянию, которое за исключением специфических ситуаций должно достигаться в определенный момент времени. Обязанность следить за адекватностью результатов целиком возлагается на пользователя. Вместе с тем весьма показательно получение результатов по прошествии продолжительного периода. По степени их адекватности можно судить о корректности граничных условий.

- Временной инкремент – временной интервал, который используется в ходе расчета (чем меньше шаг, тем точнее расчет). Однако с учетом того, что тело не влияет на окружающую среду и граничные условия действуют в течение всего рассматриваемого периода времени, модель тепловых явлений COSMOSWorks, по сути, линейна (несмотря на наличие нелинейных членов в зависимостях, например, для излучения). Из этого следует, что увеличение шага не приводит к расходимости итерационного процесса, а следовательно, критический рост ошибки не наблюдается.

- Начальная температура – температура модели в начальный момент времени. Если же для каких-либо деталей в целом или их элементов (граней, ребер, вершин) задано граничное условие «Температура», то в расчете будут использоваться заданные там величины.

 

 

Рисунок 4.2 – Окно для настройки параметров теплового анализа конструкции

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: