 |
Электрический ток в жидкостях и газах
|
|
|
|
Тема 5
Работа и мощность электрического тока
Работа электрического тока на участке цепи определяется формулой
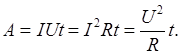
Для замкнутой цепи закон Ома имеет вид

где Е – э.д.с. генератора,
R – внешнее сопротивление,
r – внутреннее сопротивление генератора.
Полная мощность, выделяемая в цепи

Задача 43
Имеются три 110-вольтовых электрических лампочки, мощности которых равны Р1=Р2 =40 Вт и Р3 =80 Вт. Как надо включить эти лампочки, чтобы они давали нормальный накал при напряжении сети U =220 В? Начертить схему. Найти токи I1, I2, I3, текущие через эти лампочки, при нормальном накале.
| Дано: Р1=Р2 =40 Вт Р3 =80 Вт U0 =220 B U =110 B | Решение:
Сопротивление лампочек определим по формуле
 (1) (1)
|
| I1, I2, I3 –? | Общее сопротивление двух параллельно соединен |
ных лампочек с учетом того, что
Р3=2Р2,
 будет равно
будет равно
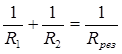 и Rэкв=R3.
и Rэкв=R3.
Отсюда напряжение в цепи будет:
IR3+Irэкв=U0.
I=const, т.к. соединение последовательное.
2U=U0
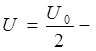 напряжение на лампочках.
напряжение на лампочках.
По закону Ома для участка цепи ток на лампочке I3 будет равен

Перепишем данное выражение с использованием формулы (1)
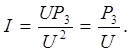
Ток на лампочках Л1 и Л2, будет равным, т.к.
U1=U2 и R1=R2,
т.е. с использованием формулы (1) получаем, что

Вычисления:
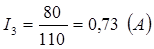
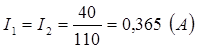
Ответ: для нормального накала нити лампочки с предложенными эксплуатационными условиями токи на лампочках Л1, Л2, Л3 соответственно равны I1=I2 =0,365 A, I3 =0,73 A.
Задача 44
В лаборатории, удаленной от генератора на расстояние
l = 100 м, включили электрический нагревательный прибор, потребляющий ток I =10 A. На сколько понизилось напряжение U на зажимах электрической лампочки, горящей в этой лаборатории, если сечение медных проводящих проводов S =5 мм2?
Дано:
l =100 м
I =10A
S =5 мм2

| Решение:
Общая длина проводов в цепи равна 2l. Сопротивление проводов найдем из формулы
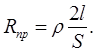 (1) (1)
|
| U –? |
На схеме в цепи сопротивление проводов обозначается резистором Rэкв.пр . До подсоединения электрического нагревательного прибора ток на резисторе Rэкв.пр. и лампочке равен
|
|
|
I1=I2=I,
т.к. соединение последовательное. Напряжение на зажимах лампочки найдем из формулы:
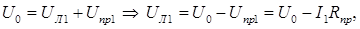 (2)
(2)
 где U0 численно равно э.д.с. источника, т.к. внутреннее сопротивление r=0, отсюда U0=const.
где U0 численно равно э.д.с. источника, т.к. внутреннее сопротивление r=0, отсюда U0=const.
Рассмотрим второй случай, напряжение на зажимах лампочки найдем из формулы:
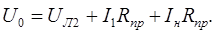
Отсюда
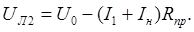 (3)
(3)
Найдем


вычтя почленно уравнения (2) и (3), получаем
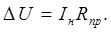
С учетом формулы (1), получаем
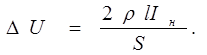
Вычисления:
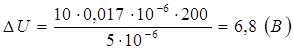
Ответ: напряжение на зажимах лампочки понизится на DU =6,8 В.
Задача 45
От батареи с э.д.с. Е =500 В требуется передать энергию на расстояние l =2,5 км. Потребляемая мощность Р =10 кВт. Найти минимальные потери мощности в сети, если диаметр медных подводящих проводов d =1,5 см.
Дано:
Е =500 В
l =2500 м
d =0,015 м
Р =104 Вт

| Решение:
Общая длина проводов 2l. Сопротивление проводов найдем из формулы
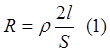
|
| DР –? | Силу тока в цепи найдем из формулы: |
 (2)
(2)
Минимальная потеря мощности DР в цепи может быть найдена из формулы
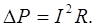 (3)
(3)
Подставляем (1) и (2) в (3), получаем
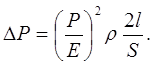 (4)
(4)
Площадь поперечного сечения проводника
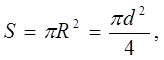 (5)
(5)
где R – радиус сечения.
Подставим (5) в (4), получаем

Вычисления:
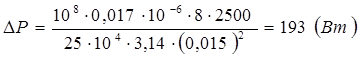
Ответ: минимальная потеря мощности в сети равна 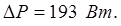
Задача 46
Элемент с эдс Е =6В дает максимальный ток I =3 А. Найти наибольшее количество теплоты, которое может быть выделено на внешнем сопротивлении в единицу времени.
| Дано: Е =6 В I =3 А | Решение: По закону Ома для полной цепи |

| 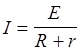
|
ток максимален, когда R=0 (внешнее сопротивление).
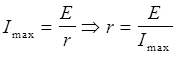 (1)
(1)
Напряжение на зажимах источника, замкнутого проводником на сопротивление R, равно

 (2)
(2)
Количество теплоты Qt, выделенное во внешнем сопротивлении в единицу времени равно мощности во внешнем участке цепи
|
|
|
P=IU (3)
подставим (2) в (3), получаем
P(I) = P= I(E-Ir)=IE - I2r (4)
Для нахождения максимальной мощности во внешнем участке цепи необходимо найти производную выражения P=(I) по переменной I и приравнять полученное выражение к нулю.
P¢(I) = E-2Ir =0
E-2IrÞ 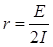 (5)
(5)
При токе
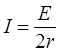 (6)
(6)
мощность максимальна при Rобщ=2r. Тогда Rвнеш=r. Подставим (6) в (4) при R=r.
Получаем
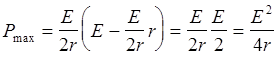
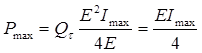
Вычисления:
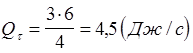
Ответ: наибольшее количество теплоты, которое может быть выделено на внешнем сопротивлении в единицу времени, составляет 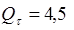 Дж/с.
Дж/с.
Задача 47
На рисунке дана зависимость полезной мощности Р от тока I цепи. По данным этой кривой найти внутреннее сопротивление r и эдс Е элемента. Построить график зависимости от тока I в цепи кпд h элемента и падение потенциала U во внешней цепи.
| Дано: Imax =5 A Pmax =5 Вт | Решение: Во внешнем участке цепи выделяется мощность |
| r, E, h(I), U(I)-? |  (1) (1)
|
 Для нахождения максимальной мощности найдем производную выражения (1) по переменной I и приравняем найденное выражение к нулю
Для нахождения максимальной мощности найдем производную выражения (1) по переменной I и приравняем найденное выражение к нулю
P¢(I) = E-2Ir =0
E = 2Ir
При токе
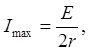 (2)
(2)
т.е. мощность максимальна при R=r
Подставим полученное выражение в (1), отсюда
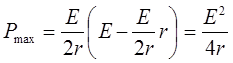 (3)
(3)
Из графика видно, что Pmax= 5 Вт, а сила тока при этом
Imax = 5 A. Подставим эти значения в (2)и (3)
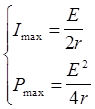 ;
; 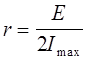 ;
; 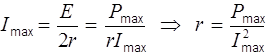 , (4)
, (4)
отсюда
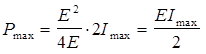
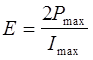 (5)
(5)
Падение потенциала U во внешней цепи выражается формулой
U = E - Ir (6)
- график зависимости - прямая.
Подставим (5) и (4) в (6), получаем:
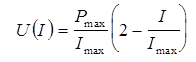
График зависимости U = U (I)
 Из графика видно, что
Из графика видно, что
1) при разомкнутой цепи (I=0) U=E
2) при токе в I=10 А падение потенциала U во внешней цепи равно U=0 В.
КПД элемента равен отношению мощности Р1, выделяемой внешним участком электрической цепи (полезной мощности), к полной мощности, развиваемой источником,

По определению
P1 = UI и P = EI.
Отсюда
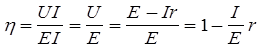
Используем формулы (5) и (4), перепишем зависимость h(I)
График зависимости h = h(I)
 Зависимость h(I) - линейная.
Зависимость h(I) - линейная.
Из графика видно, что при R=0, т.е. внешнее сопротивление равно нулю, наступает короткое замыкание  и КПД источника равен нулю.
и КПД источника равен нулю.
Вычисления:


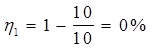
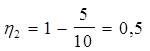 или 50%
или 50%
Ответ: напряжения равны соответственно U1=0 В, U2=1 В, КПД источника соответственно равны h1=0%, h2=50%.
Задача 48
Эдс батареи Е =120 В, сопротивление R3 =30 Ом, R2 =60 Ом. Амперметр показывает ток I = 2 A. Найти мощность Р, выделяющуюся в сопротивлении R1.
| Дано: Е =120 В R3 =30 Ом R2 =60 Ом I =2 А | Решение: Мощность Р1, выделяющуюся на сопротивлении R1, определяем формулой P=UI (1) По закону Ома для участка цепи |
| Р =? | U3=R3I |
т.к. R1 и R2 соединены параллельно, то
|
|
|
I1 +I2 = I (2)
По условию внутреннее сопротивление r=0 и тогда
U12=E-U3
U12=E-R3I (3)
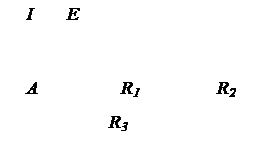 Т.к. соединение сопротивлений R1 и R2 параллельное, то
Т.к. соединение сопротивлений R1 и R2 параллельное, то
U1= U2= U12 (4)
По закону Ома для участка цепи
U1=R1I1 (5)
U2=R2I2. (6)
Отсюда
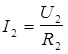 . (7)
. (7)
Подставим (4) в (5), получаем:
 . (8)
. (8)
Подставим (6), (8) в (7), получим

Вычисления:
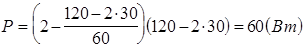
Ответ: мощность, выделяемая в сопротивлении R1 , составляет Р =60 Вт.
Задача 49
Две электрические лампочки с сопротивлениями R1 =360 Ом и R2 =240 Ом включены в сеть параллельно. Какая из лампочек потребляет большую мощность и во сколько раз?
| Дано: R1 =360 Ом R2 =240 Ом | Решение: Мощность, потребляемую лампочкой, можно выразить через формулу |
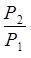 -? -?
| 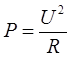 , ,
|
так как лампочки включены параллельно, напряжение, приложенное к ним, одинаково
U1 = U2 = U.
 Отсюда мощность потребляемая первой лампочкой:
Отсюда мощность потребляемая первой лампочкой:
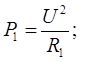 (1)
(1)
второй лампочкой:
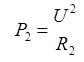 . (2)
. (2)
Найдем отношение 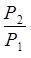 , разделив почленно формулу (1) и (2). Получаем
, разделив почленно формулу (1) и (2). Получаем
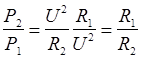 .
.
Вычисления:
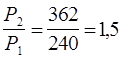
Ответ: в 1,5 раза большую мощность потребляет лампочка с меньшим сопротивлением.
Задача 50
Какую мощность Р потребляет нагреватель электрического чайника, если объем V =1л воды закипает через время t =5 мин? Каково сопротивление R нагревателя, если напряжение в сети U =120 В? Начальная температура воды t0 =13,50C.
Дано:
t0 =13,50C
t =1000C
t =5 мин
U =120 В
V =10-3 м3
с =4190 Дж/кг·°С
r= 10 
| Решение: Из курса термодинамики нам известно, что количество теплоты, которую надо затратить при нагревании тела массой m от температуры t0 до температуры t, определяется формулой Q = mc(t - t0), (1) c - удельная теплоемкость данного вещества. Согласно закона Джоуля-Ленца |
| P, R -? | 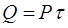 (2) (2)
|
 Исходя из того, что выделение теплоты на нагревателе электрического чайника идет на увеличение температуры воды от t0 до t, можно приравнять выражения (1) и (2), получаем
Исходя из того, что выделение теплоты на нагревателе электрического чайника идет на увеличение температуры воды от t0 до t, можно приравнять выражения (1) и (2), получаем
 . (3)
. (3)
Мощность, потребляемую чайником, можно записать в виде
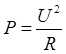 . (4)
. (4)
Подставим (4) в (3), получаем
 (5)
(5)
Перепишем формулы (3) и (5) с учетом формулы, m=rV:
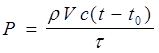
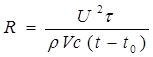 .
.
|
|
|
Вычисления:
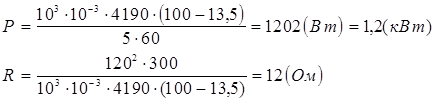
Ответ: нагреватель электрического чайника потребляет мощность Р =1,2 кВт, а сопротивление R нагревателя равно R = 12 Ом.
Задача 51
Нагреватель электрического чайника имеет две секции. При включении одной из них вода в чайнике закипает через t1 =15 мин, при включении другой – через t2 =30 мин. Через какое время закипит вода в чайнике, если включить обе секции: а) последовательно; б) параллельно?
| Дано: t1 =15 мин t2 =30 мин | Решение: Если участок цепи не содержит источников тока, то количество теплоты выделяющееся, на этом участке, |
| tа, tb –? | можно определить по формуле |
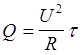 ,
,
где U - напряжение, подводимое к участку.
Количество теплоты, которое надо сообщить воде в чайнике, чтобы она закипела, одинаково независимо от включения секций. В формуле будут только две меняющиеся переменные: R и t, т.е. при последовательном и параллельном соединении секций формула (1) примет вид

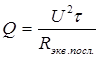 и
и 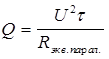 .
.
Приравняв отношения 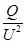 , полученные при различных подключениях секций, получим:
, полученные при различных подключениях секций, получим:
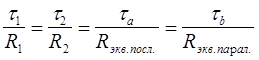 (2)
(2)
где R1 и R2 - сопротивления первой и второй соответственно соединенных секций;
Rэкв.посл. - эквивалентное сопротивление двух последовательно соединенных секций;
Rэкв.парал. - эквивалентное сопротивление двух параллельно соединенных секций.
1) Рассмотрим отношение


По определению
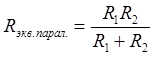 .
.
Отсюда
 .
.
Из соотношений (2) найдем, что отношение 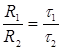 , с учетом этого
, с учетом этого
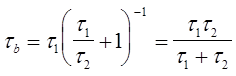 .
.
2) Рассмотрим отношение
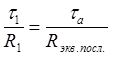
 (3)
(3)
Зная, что Rэкв.посл. = R1 + R2,
перепишем выражение (3)
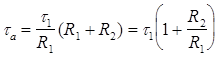 .
.
Из соотношений (2) найдем, что отношение 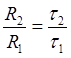 , с учетом этого
, с учетом этого
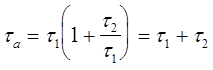 .
.
Вычисления:
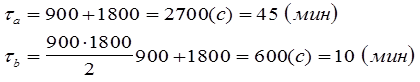
Ответ: при последовательном и параллельном соединениях нагревателей время, необходимое для закипания, составляет соответственно tа =45 мин, tb =10 мин.
Тема 6
Правила Кирхгофа
Для разветвленных цепей имеют место два закона Кирхгофа:
первый закон Кирхгофа - алгебраическая сумма токов, сходящихся в узле, равна нулю:

второй закон Кирхгофа - в любом замкнутом контуре алгебраическая сумма падений потенциала на отдельных участках цепи равна алгебраической сумме э.д.с., встречающихся в этом контуре:
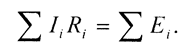
При применении законов Кирхгофа надо руководствоваться следующими правилами:
на схеме произвольно указываются стрелками направления токов у соответствующих сопротивлений. Обходя контур в произвольном направлении, будем считать положительными те токи, направления которых совпадают с направлением обхода, и отрицательными те направления которых противоположны направлению обхода.
Положительными э.д.с. будем считать те э.д.с., которые повышают потенциал в направлении обхода, т.е. э.д.с. будет положительной, если при обходе придется идти от минуса к плюсу внутри генератора.
|
|
|
Напомним
 В результате решения составленных уравнений определяемые величины могут получиться отрицательными. Отрицательное значение тока указывает на то, что фактическое направление тока на данном участке цепи обратно принятому.
В результате решения составленных уравнений определяемые величины могут получиться отрицательными. Отрицательное значение тока указывает на то, что фактическое направление тока на данном участке цепи обратно принятому.
Задача 52
Найти токи Ii в отдельных ветвях мостика Уинстона при условии, что через гальванометр идет ток Ir =0. Э.д.с. элемента Е =2,2 В. Сопротивления резисторов Ri =30 0м, R2 =45 0м и R3 =200 0м.
| Дано: Е =2,2 В R1 =30 0м R2 =45 0м R3 =200 0м Ir =0 | Решение: Обозначим направление токов, выберем направление обхода всех контуров по часовой стрелки. По первому закону Кирхгофа составим уравнения для узла В и D, пользуясь условием, говорящем о том, что Ir =0: |
| I1, I2, I3, I4 –? | узел В: |
 I1 - I2 = 0 Þ I1 = I2 (1)
I1 - I2 = 0 Þ I1 = I2 (1)
узел D:
I3-I4= 0 Þ I3 = I4 (2)
По второму правилу Кирхгофа составим уравнения для контуров BСDВ и АВDА.
Контур BСDВ:
I2R2 – I4R4 = 0 (2¢)
Данное выражение получилось таким из условия, что
r = 0 (3)
Контур АВDА:
I1R1 - I3R3= 0 (4)
Контур АВСEFА:
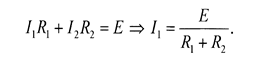 (5)
(5)
Преобразуем выражение (4) и подставим формулу (5), получаем
I1R1 = I3R3

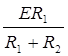 = I3R3 Þ
= I3R3 Þ 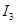 =
= 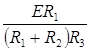
Вычисления:
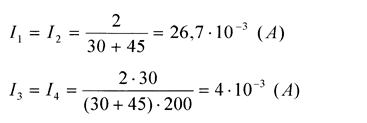
Ответ: токи в ветвях с сопротивлениями R1 и R2 равны I1 = I2 =26,7·l0-3 А, токи в ветвях с сопротивлениями R3 и R4 равны I3 = I4 =4·l0-3 А.
Задача 53
Э.д.с. элементов E1 =2,l В и E2 =l,9 В, сопротивления R1 =45 0м, R2 =10 0м и R3 =10 0м. Найти токи Ii во всех участках цепи.
| Дано: E1 =2,l В Е2 =1,9 В R1 =45 0м R2 =10 0м R3 =10 0м | Решение: Обозначим направление токов как показано на рисунке. Направление обхода контура показано на рисунке. По первому правилу Кирхгофа составим уравнение для узла С: -I1 + I3 + I2 = 0 Þ I1 = I2 + I3 |
| I1, I2, I3 –? |
 По второму правилу Кирхгофа составим уравнения для контуров АВСА и ACDA:
По второму правилу Кирхгофа составим уравнения для контуров АВСА и ACDA:
контур АВСА: I3R3 + I1R1 = E1,
контур ACDA: I1R1 + I2R2 = E2.
Из полученных выражений составим систему уравнений:

отсюда
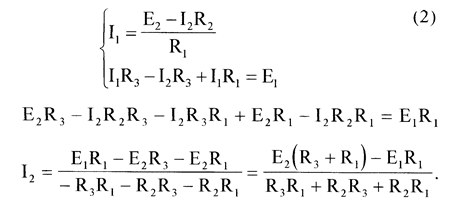
Подставим полученное выражение в (1), получаем:
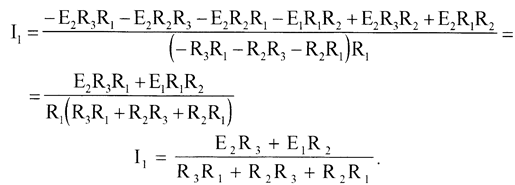
Ток, текущий в ветви с сопротивлением R3, найдем из формулы (2), как
I3 = I1 - I2.
Вычисления:


Ответ: токи в участках цепи с сопротивлениями R1, R2, R3 соответственно равны I1 =0,04 А, I2 =0,01 А, I3 =0,03 А.
Задача 54
Два элемента с одинаковыми э.д.с. E1=E2=2 В и внутренними сопротивлениями r1 =l 0м и r2 =2 0м замкнуты на внешнее сопротивление R. Через элемент с э.д.с. E1 течет ток I1 =l А. Найти сопротивление R и ток I2, текущий через элемент с э.д.с. E2. Какой ток I течет через сопротивление R?
| Дано: E1=E2=2 В r1 =l 0м r2 =2 0м I1 =l А | Решение: Обозначим направление токов как показано на рисунке, выберем направление обхода контура. По первому правилу Кирхгофа составим уравнение для узла B. |
| R, I2, I –? | Узел B: |
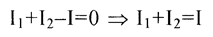 (1)
(1)
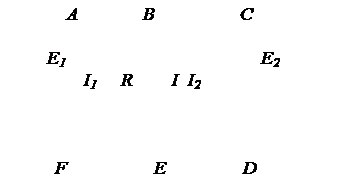 По второму правилу Кирхгофа составим уравнения для контуров ABEFA и BCDEB.
По второму правилу Кирхгофа составим уравнения для контуров ABEFA и BCDEB.
Контур ABEFA:
I1r1+IR=E1 (2)
Контур BCDEB: I2r2+IR=E2.
Из ранее полученных выражений составим
систему уравнений:
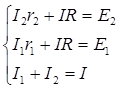
Отсюда
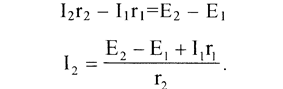 (3)
(3)
Подставим выражение (3) в (1), получаем
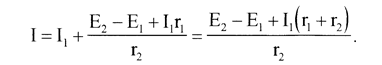 (4)
(4)
Подставим выражение (4) в (2), получаем
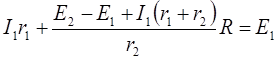

Вычисления:
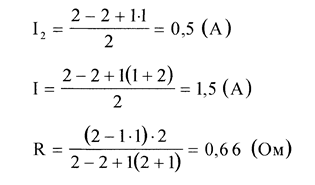
Ответ: внешнее сопротивление R равно R =0,66 0м, сила тока, текущего через элемент с э.д.с. Е2 равна I2 =0,5 А, сила тока, идущего через внешнее сопротивление R равна I =1,5 А.
Задача 55
Батареи имеют э.д.с. E1 =110 В и Е2 =220 В, сопротивления R1 = R2 =100 0м, R3 =500 0м. Найти показания амперметра.
| Дано: E1 = 110 В Е2 =220 В R1=R2 =100 Ом R3 =500 Ом | Решение: Амперметр покажет величину тока, текущего через сопротивление R1, т.е. ток I1, т.к. амперметр и сопротивление R1 соединены последовательно. |
| I1 –? |
 Обозначим направление токов, выберем направления обходов контуров как показано на рисунке. По первому правилу Кирхгофа составим уравнение для узла E:
Обозначим направление токов, выберем направления обходов контуров как показано на рисунке. По первому правилу Кирхгофа составим уравнение для узла E:
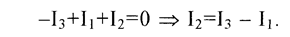
По второму правилу Кирхгофа составим уравнения для контуров ABEFA и BCDEB:
контур ABEFA: I1R1+I3 R3=E1,
контур BCDEB: I2R2+I3R3=E2,
Из ранее полученных уравнений составим систему уравнений
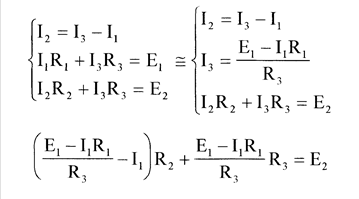
(E1 - I1R1 - I1R3) R2 + + R3E1 - I1R1R3 = E2R3
Отсюда
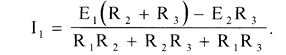
Вычисления:
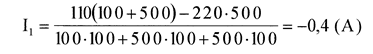
Отрицательный знак у тока I1 указывает на то, что направление тока нами было взято неправильно, направление тока будет от F к А.
Ответ: амперметр покажет силу тока, равную I1 =0,4А.
Задача 56
Батареи имеют э.д.с. E1 =2 В и E2 =1 В, сопротивления R1 =l кОм, R2 =0,5 кОм и R3 =0,2 кОм, сопротивление амперметра RA =0,2 êÎì. Найти показания амперметра.
| Дано: E1=2 В Е2 =1 В R1 = 103Ом R2 =500 Ом R3 =200 Ом ra =200 Ом | Решение: Амперметр будет показывать величину тока, текущего через сопротивление r3, т.к. сопротивления r3 и ra подключены последовательно, т.е. задача сводится к нахождению I3. Обозначим направление токов и направления обходов контуров как показано на рисунке. |
| IА –? | По первому правилу Кирхгофа составим уравнение для узла Е: |
I2+I3-I1=0.
По второму правилу Кирхгофа составим уравнения для контуров АВЕFA и BCDEb,
Контур ABEFA: I2R2+I1 R1=E1
Контур BCDEB: I3R3+IR1+I3 RA=E2
Используя ранее полученные уравнения, составим систему уравнений:

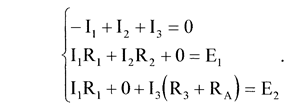
Составим матрицу из данной системы:
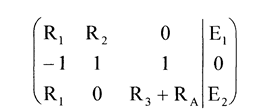
Подставим числовые значения и решим данную матрицу методом, используя метод Гаусса.
Вычисления:

Отсюда
1,1× I3 = -0,0005
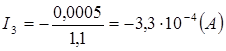
Отрицательный знак у тока I3 указывает на то, что направление тока нами было выполнено неправильно и ток I3 течет в обратном направлении.
Ответ: амперметр показывает величину силы тока, равную I =3,3·10 -4 A.
Задача 57
Батареи имеют э.д.с. E1=E2. Сопротивление R1=R2 =100 Ом. Сопротивление вольтметра RV =150 Ом. Показания вольтметра U =l50 В. Найти э.д.с. батарей.
| Дано: E1 = Е2 R1 = R2 =100 Ом RV =150 Ом U =l50 В | Решение:
Зная, что показание вольтметра есть произведение силы тока в этой цепи на его собственное сопротивление получаем, что
 (1) (1)
|
| E1 = Е2 –? | Обозначим направления токов как показано на |
 рисунке, выберем направления обхода контуров.
рисунке, выберем направления обхода контуров.
По первому правилу Кирхгофа составим уравнение для узла Е:
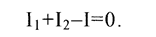 (2)
(2)
Используя выражение (1), преобразуем (2), получаем, что
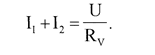 (3)
(3)
По второму правилу Кирхгофа составим уравнения для контуров.
ABEA: I1R1+IRV=E1,
BCEB: I2R2+IRV=E2,
Используя формулу (1), получаем, что
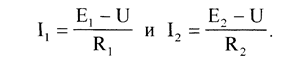
Подставим полученные формулы в (3), получаем
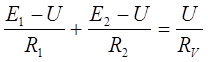
Используя условие задачи, говорящее о равенстве E1=E2, получаем

Вычисления:
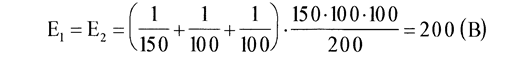
Ответ: батареи, включенные в цепь, будут иметь э.д.с. равную E1=E2= 200 B.
Задача 58
Элементы имеют э.д.с. E1=E2 =l,5 В и внутренние сопротивления r1=r2 =0,5 Oм. Сопротивления R1=R2 =2 Oм и R3 =1 0м. Сопротивление амперметра RA =3 Oм. Найти показание амперметра.
| Дано: E1 = Е2 = 1,5 B r1=r2 =0,5 Oм R1 = R2 =100 Ом R3 =1 Ом RA =3 Ом | Решение: Рассмотрим эквивалентную схему, в которой все сопротивления заменим на одно эквивалентное сопротивление и найдем силу тока I в такой цепи, такой же ток будет на резисторе R1 и R2 и на Rобщ, т.к. они соединены |
| IA –? | последовательно, где Rобщ - эквивалентное |
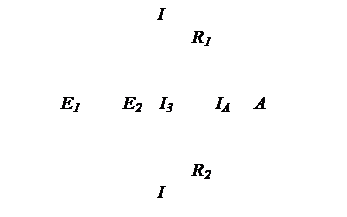 сопротивление резистора и амперметра, R3 и RA.
сопротивление резистора и амперметра, R3 и RA.
Из параллельности их соединения следует, что
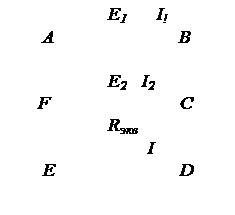
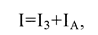 (1)
(1)
где I3 - сила тока на резисторе R3, IA - сила тока на амперметре. Начертим эквивалентную схему.
Обозначим направления токов и обхода контуров как показано на рисунке.
По первому правилу Кирхгофа напишем уравнения для узла С:
I1+I2-I=0 Þ I=I1+I2. (2)
По второму правилу Кирхгофа напишем уравнения для контуров abdeA и FCDEF.
ABDEA: I1r1+IR=E1,
FCDEF: I2r2+IR=E2.
Отсюда выразим I1 и I2 и подставим их выражения в (2), получаем:
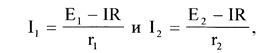
отсюда
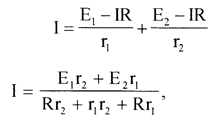 (3)
(3)
где R = Rэкв.
Т.к. сопротивления R3 и ra соединены параллельно, то
U3 = UA, т.е.
 (4)
(4)
Подставим (4) в (1), получаем:
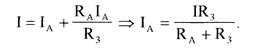 (5)
(5)
Найдем Rэкв
1) из параллельности соединения R3 и ra их
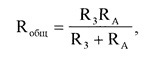
2) из последовательности соединения R1, R2 и Rобщ их
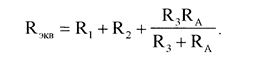 (6)
(6)
Подставляя (6), (3) в (5), получаем

Вычисления:
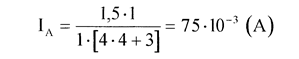
Ответ: показание амперметра в данной ветви цепи будет IA =75·10-3А.
Задача 59
Элемент имеет э.д.с. Е =200 В. Сопротивление R1 =2 кОм и R2=3 кОм. Сопротивление вольтметров RV1 =3 кОм и RV2 =2 кОм. Найти показания вольтметров V1 и V2, если ключ К: а) разомкнут, б) замкнут. Задачу решить, применяя правила Кирхгофа.
| Дано: R1 =2000 Oм R2 =3000 Oм RV1 =3000 Oм RV2 =2000 Oм Е =200 В | Решение: а) Рассмотрим случай, когда ключ К разомкнут. Показание вольтметра U складывается из произведения собственного сопротивления вольтметра на силу тока, протекающего по нему. |
| U1,U2 -?–? |
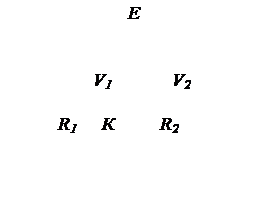 Ток на первом и втором вольтметрах будет равен по величине, т.к. они соединены последовательно, следовательно, их можно заменить эквивалентным сопротивлением и найти ток на нем. Аналогично заменяем сопротивления R1 и R3 эквивалентным сопротивлением. Отсюда эквивалентная схема примет вид:
Ток на первом и втором вольтметрах будет равен по величине, т.к. они соединены последовательно, следовательно, их можно заменить эквивалентным сопротивлением и найти ток на нем. Аналогично заменяем сопротивления R1 и R3 эквивалентным сопротивлением. Отсюда эквивалентная схема примет вид:
 Здесь
Здесь
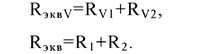 (1)
(1)
Обозначим направления токов и обхода контуров как показано на рисунке.
По первому правилу Кирхгофа напишем уравнение для узла С:

По второму правилу Кирхгофа напишем уравнение для контура ABCFА.
ABCFA: I1RэквV=E.
Или, с использованием (1), получаем:
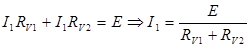 (2)
(2)
Получив ток, проходящий через вольтметры, найдем их показания:
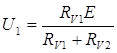
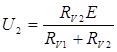
б) Рассмотрим второй случай, когда ключ К замкнут. Преобразуем данную схему в более удобную для рассмотренного случая:
Токи, текущие через Rэкв1 и Rэкв2, равны, т.к. они соединены последовательно.
При этом заменим параллельное соединение R1 и RV1 их эквивалентным сопротивлением Rэкв1 зная что показание вольтметра будет равно разности потенциалов на этом эквивалентном сопротивлении
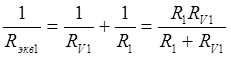 (3)
(3)
Аналогичную замену произведением для параллельного соединения сопротивлений R2 и RV2, зная, что вольтметр будет показывать разность потенциалов на этом эквивалентном сопротивлении Rэкв2
 (4)
(4)
 Применяя второе правило Кирхгофа напишем уравнение для контура ABCDA:
Применяя второе правило Кирхгофа напишем уравнение для контура ABCDA:
IR экв1 + IR экв2 = Е (5)
Подставим (3), (4) в (5), получаем

Отсюда

Из ранее предложенного рассуждения показания вольтметров будут определяться по формуле, как
U 1 = IR экв1
U 1 = IR экв2
Используя формулы (3) и (4), получаем

Вычисления:
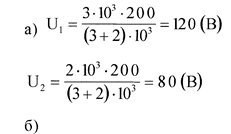
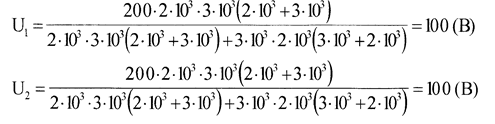
Ответ: при разомкнутом ключе вольтметры показывают напряжения U1 =120 В и U2 =80 В. При замкнутом ключе — U1 = U2 =100 В.
Тема 7
Электрический ток в жидкостях и газах
Для электрического тока имеют место два закона Фарадея:
первый закон Фарадея - масса вещества, выделившаяся при электролизе прямо пропорциональна прошедшему заряду:
m=kIt=kq,
где q - количество электричества, прошедшего через электролит,
k - электрохимический эквивалент.
Второй закон Фарадея - электрохимический эквивалент пропорционален химическому эквиваленту:
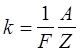
где А - молярная масса,
Z - валентность,
F =96,5-l03 Кл/моль - постоянная Фарадея.
|
|
|


