 |
Удельная проводимость электролита определяется формулой
|
|
|
|

a - степень диссоциации,
С [моль/м3] - молярная концентрация,
Z - валентность,
F - постоянная Фарадея,
u +и u - [м /(В-с)] - подвижность ионов.
При этом a=nq/nn - отношение числа диссоциированных молекул в единице объема к числу всех молекул растворенного вещества в этом объеме. Величина n=CZ [моль/м3] - называется эквивалентной концентрацией, а величина L=s/h [м2/(Ом·моль)] -эквивалентной проводимостью.
При небольших плотностях тока, текущего в газе, имеет место закон Ома:
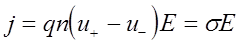
где Е - напряженность поля,
s - удельная проводимость газа,
q - заряд иона,
п [м-3]- число ионов каждого знака (число пар ионов), находящихся в единице объема газа. При этом

где N [м-3с-1] - число пар ионов, создаваемых ионизирующим агентом в единице объема в единицу времени,
g [м3/с] - коэффициент рекомбинации.
Плотность тока насыщения в газе определяется формулой
JH = Nqd
где d - расстояние между электродами.
Чтобы вырваться из металла наружу, электрон должен обладать кинетической энергией

где А - работа выхода электрона из данного металла.
Плотность тока насыщения при термоэлектронной эмиссии определяется формулой
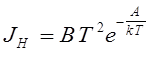
где Т - термодинамическая температура катода,
А - работа выхода,
k = 1,38·10-23 Дж/К - постоянная Больцмана,
В [А/(м2·К2)] - эмиссионная постоянная, разная для различных металлов.
Задача 60
При электролизе медного купороса за время t =l ч выделилась масса т =0,5 г меди. Площадь каждого электрода S =75 см2. Найти плотность тока j.
| Дано: t =3600 с т =5·10-4 кг S =75·10-4 м2 Z =2 А =63,5·10-3 кг/моль F =96,5·103 Кл/моль | Решение:
Плотность электрического тока определяется формулой
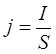 (1)
По первому закону Фарадея - масса вещества, выделившегося при электролизе (1)
По первому закону Фарадея - масса вещества, выделившегося при электролизе
|
| j –? |  (2) (2)
|
По второму закону Фарадея -электрохимический эквивалент пропорционален химическому эквиваленту
|
|
|

 (3)
(3)
Подставляя формулу (3) в (2) получившееся выражение подставляем в формулу (1) получаем

Вычисления:

Ответ: плотность тока в электролите j =56,3 А/м2.
Задача 61
Две электролитические ванны с растворами AgNO3 и CuSO4 соединены последовательно. Какая масса m2 меди выделится за время, в течение которого выделилась масса серебра, равная m1 =180 мг?
| Дано: mAg =18·10-7 кг kAg = 1,11·10-6 кг/Кл kCu =3,3·10-7 кг/Кл t1=t2 | Решение: Ток, текущий через ванны с растворами, равен, т.к. они соединены последовательно и равен I. По первому закону Фарадея, применительно |
| mCu –? | к раствору AgNO3, найдем, |
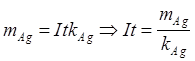 (1)
(1)
 По первому закону Фарадея применительно к раствору CuSO4, найдем, что
По первому закону Фарадея применительно к раствору CuSO4, найдем, что
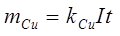 (2)
(2)
Подставим выражение (1) в формулу (2), получаем

Вычисления:
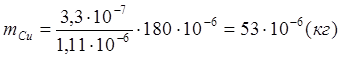
Ответ: за одинаковое время в последовательно соединенных ваннах с растворами AgNO3 и CuSO4 выделилось т2 =53·10-6 кг меди во втором растворе.
Задача 62
Какую электрическую энергию W надо затратить, чтобы при электролизе раствора AgNO3 выделилось т =500 мг серебра? Разность потенциалов на электродах U =4 В.
| Дано: mAg =500·10-6 кг U =4 В kAg = 11,18·10-6 кг/Кл | Решение: Энергия, необходимая для выделения массы m вещества при электролизе W - IUt, (1) |
| W –? | где U - приложенная разность потенциалов. |
 По первому закону Фарадея:
По первому закону Фарадея:
 (2)
(2)
Подставим (2) в (1), получаем

Вычисления:

Ответ: для выполнения поставленных в задаче целей надо затратить электрическую энергию, равную W =l,79·103 Дж.
Задача 63
Через раствор азотной кислоты пропускается ток I =2А. Какое количество электричества q переносится за t =l мин ионами каждого знака?
| Дано: I =2 А t =60 с и+ =32,6·10-8 м2/(В·с) и_ =6,4·10-8 м2/(В·с) | Решение: Суммарный заряд, прошедший через электролит q=q++q_. С другой стороны |
| q+, q- –? | q=It. (1) |
Отсюда
q++q_=It
При небольших плотностях тока имеет место соотношения

q - заряд иона,
|
|
|
n - число ионов каждого знака, находящихся в единице объема электролита, Е - напряженность поля.
 Отсюда составим отношение
Отсюда составим отношение
 (2)
(2)
Мы знаем, что
q=It=jSt
Количество электричества q+ и q_, переносимое за время t ионами каждого знака
q+=j+St
q-=j-St
Составим соотношение
 (3)
(3)
Приравнивая отношения (1) и (2) получаем отношение
 (4)
(4)
На основе уравнений (1) и (4) составим систему уравнений



Отсюда
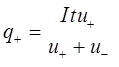
Вычисления:
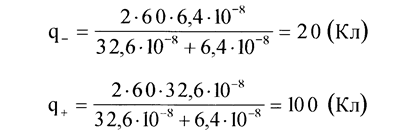
Ответ: количество электричества, переносимого за время t ионами отрицательного и положительного знака соответственно равно q_ = 20 Кл и q+ = 100 Кл.
Задача 64
Найти сопротивление R раствора AgNO3, заполняющего трубку длиной l =84 см и площадью поперечного сечения S =5 мм2. Эквивалентная концентрация раствора h =0,1 моль/л, степень диссоциации a = 8 1%.
| Дано: Z= 1 F =96,5·103 кл/моль l =84·10-2м u+ =5,6·10-3 м2/В·с и- =6,4·10-3 м2/В·с S =5·10-6ì h=100 моль/м3 a = 81% | Решение:
Сопротивление раствора:
 (1)
где s - удельная проводимость, определяемая по формуле:
s =aCZF (u+ + u_) (2)
Величина
h =cz - эквивалентная концентрация (1)
где s - удельная проводимость, определяемая по формуле:
s =aCZF (u+ + u_) (2)
Величина
h =cz - эквивалентная концентрация
|
| R-? | Отсюда |
 s =ahF(u+ + u_)
s =ahF(u+ + u_)
Подставим выражение (2) в (1), получаем

Вычисления:

Ответ: сопротивление раствора AgNO3, заполняющего трубку, равно R =180·103 0м.
Задача 65
Удельная проводимость децинормального раствора соляной кислоты s = 3,5 См/м. Найти степень диссоциации a.
| Дано: s = 3,5 См/м h = 0,1 моль/л Z = l u+ =32,6·10-3 м2/В·с и- =6,8·10-3 м2/В·с F =96,5·103 Кл/моль t = 1 | Решение:
Удельная проводимость электролита определяется формулой
s =aCZF (u+ + u_)Þ
 где
где
|
| a-? | h =cz - эквивалентная концентрация |
Вычисления:

Ответ: степень диссоциации данного раствора равна a = 9 2%.
Задача 66
К электродам разрядной трубки приложена разность потенциалов U =5 В, расстояние между ними d =10 см. Газ, находящийся в трубке, однократно ионизирован. Число ионов каждого знака в единице объема газа п =108 м-3 подвижность ионов и+ =3·10-2 м2/(В·с) и и_ =3·10-2 м2/(В·с). Найти плотность тока j в трубке. Какая часть полного тока переносится положительными ионами?
| Дано: U=5 В d =10-1 м Z= 1 п =108 м-3 u+ =3·10-2м2/В·с и- =3·10-2м2/В·с | Решение: При небольших плотностях тока, текущего в газе, имеет место закон Ома j=qn(u++u_)E. (1) По условию газ, находящийся в трубке однократно ионизирован, отсюда заряды ионов равны по модулю заряду электрона. Напряженность |
j-? 
| поля определяется формулой |
 (2)
(2)
|
|
|
Подставляя (2) в (1), получаем:

Зная, что
 j+=enu+E, (3)
j+=enu+E, (3)
j-=enu-E, (4)
найдем часть полного тока, переносимого положительными зарядами, т.е. отношение  .
.
Подставим в это выражение формулы (3) и (4). С учетом формулы (2) получаем

Вычисления:


Ответ: плотность тока в трубке равна j =2,4·10-7 А/м2, часть полного тока переносимого положительными ионами равна 
Задача 67
Площадь каждого электрода ионизационной камеры S =0,01 м2, расстояние между ними d =6,2 см. Найти ток насыщения IH в такой камере, если в единице объема в единицу времени образуется число однозарядных ионов каждого знака n =1015м-3c-2?
| Дано: S =0,01 м2 d =0,062 м n =1015м-3c-2 е = 1,6·10-19 Кл Z= 1 | Решение: По условию ионы однозарядные, т.е. имеют заряд по модулю равный заряду электрона. Плотность тока насыщения в газе определяется формулой jH=Nqd Þ jH=eNd |
| IН-? | Также плотность электрического тока: |
 ,
,
отсюда ток насыщения равен:


Вычисления:
IH= 1015·1,6·10-19·0,062·10-2=10-7 (А)
Ответ: ток насыщения в этой камере равен IH 10-7 А.
Задача 68
Найти сопротивление R трубки длиной l =84 см и площадью поперечного сечения S =5 мм2 если она заполнена воздухом, ионизированным так, что в единице объема при равновесии находится п =1013 м-3 однозарядных ионов каждого знака. Подвижность ионов u+ =1,3·10-4м2/(В·с) и u+ =1,8·10-4м2/(В·с)
| Дано: l= 0,84м S =5·10-6 м2 Z= 1 u+ =1,3·10-4м2/(В·с) и- =1,8·10-2м2/(В·с) n = 1013м-3 | Решение:
По условию ионы однозарядны, т.е. имеют заряд по модулю равный заряду электрона. Сопротивление трубки с газом определяется формулой

|
| R-? | где s - удельная проводимость газа, которая |
 может быть найдена из формулы:
может быть найдена из формулы:
s = qn (u++u-) = en (u++u-)
Подставим (2) в (1), получаем:

Вычисления:

Ответ: сопротивление трубки с воздухом будет равно R =3,4·1014 Ом.
Тема 8
Магнитное поле
По закону Био-Савара-Лапласа элемент контура dl, по которому течет ток I, создает в некоторой точке А пространства магнитное поле напряженностью

где r - расстояние от точки А до элемента тока dl,
а - угол между радиус - вектором r и элементом тока dl.
Применим закон Био-Савара-Лапласа к контурам различного вида.
|
|
|
Напряженность магнитного поля в центре кругового тока

где R - радиус кругового контура с током.
Напряженность магнитного поля, созданного бесконечно длинным прямолинейным проводником

где а - расстояние от точки, где ищется напряженность, до проводника с током.
Напряженность магнитного поля на оси кругового тока

где R - радиус кругового контура с током,
а — расстояние от точки до плоскости контура.
Напряженность поля внутри тороида и бесконечно длинного соленоида
Н=Iп,
где п - число витков на единицу длины соленоида.
Напряженность магнитного поля на оси соленоида конечной длины
 ,
,
где b1 и b 2- углы между осью соленоида и радиус - вектором, проведенным из рассматриваемой точки к концам соленоида.
Задача 69
Найти напряженности Н магнитного поля в точке, отстоящей на расстоянии а =2 м от бесконечно длинного проводника, по которому течет ток I =5 А.
| Дано: а =2 м I =5 А p =3,14 | Решение: Напряженность магнитного поля, созданного бесконечно длинным прямолинейным проводником: |
| Н-? | 
|
 Вектор
Вектор  расположен по касательной к окружности, направление определяется правилом буравчика.
расположен по касательной к окружности, направление определяется правилом буравчика.
Вычисления:

Ответ: напряженность магнитного поля в точке, отстоящей на данном расстоянии от бесконечно длинного проводника, по которому течет ток, равна Н =0,39 А/м.
Задача 70
Найти напряженность Н магнитного поля в центре кругового проволочного витка радиусом R =l с которому течет ток I =1 А.
| Дано: R =0,01 м I =1 А | Решение:
Напряженность магнитного поля в центре кругового тока: 
|
| Н-? |
 Вычисления:
Вычисления:

Вывод данной формулы
В этом случае все элементы проводника перпендикулярны к радиус - вектору и sin j =l. Расстояние всех элементов провода до центра круга одинаково и равно радиусу круга R. Поэтому, используя закон Био-Савара - Лапласа получаем:

Все элементы тока создают магнитное поле одинакового направления, перпендикулярное к плоскости витка, и поэтому полная напряженность поля в центре кругового витка равна

где l - длина окружности.
Направление магнитного поля находим по правилу правого буравчика.
Ответ: напряженность магнитного поля в центре кругового проволочного витка равна 50 А/м.
Задача 71
На рисунке изображены сечения двух прямолинейных бесконечно длинных проводников с токами. Расстояние между проводниками АВ =10 см, токи I1 =20A и I2 =30A. Найти напряженность Н магнитного поля, вызванного токами I1 и I2 в точках M1, М2, М3. Расстояния M1а =2 см, АМ2 =4 см, ВМ3 = 3см.
| Дано: M1а =2 см АМ2 =4 см ВМ3 = 3см I1 =20A I2 =30A АВ =10 см | Решение:
Напряженность магнитного поля, создаваемая бесконечно длинным прямолинейным проводником:
 1) Найдем напряженность магнитного поля, вызванного токами I1 и I2 в точке M1. Согласно принципу
1) Найдем напряженность магнитного поля, вызванного токами I1 и I2 в точке M1. Согласно принципу
|
| Н1, Н2, Н3-? | суперпозиции, в точке M1 напряженность |

|
|
|
Н1 и Н2 - напряженности магнитных полей, создаваемые в этой точке токами I1 и I2 соответственно.
Спроецируем данные вектора на ось х, получаем что
Н = Н1 - Н2
Найдем Н1 и Н2, подставляя данные из условия задачи в формулу (1), т.е.


Тогда


2)  Найдем напряженность магнитного поля, вызванного токами Н1 и Н2 в точке М2. Согласно принципу суперпозиции, в точке М2 напряженность
Найдем напряженность магнитного поля, вызванного токами Н1 и Н2 в точке М2. Согласно принципу суперпозиции, в точке М2 напряженность

где Н1 и Н2 - напряженности магнитных полей, создаваемые в этой точке токами I1 и I2 соответственно.
Спроецируем данные вектора на ось х, получаем что
Н = Н1 + Н2
Найдем Н1 и Н2, подставляя данные из условия задачи в формулу (1), т.е.

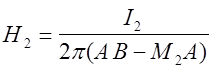
Тогда


3) Найдем напряженность магнитного поля, вызванного токами I1 и I2 в точке М3. Согласно принципу суперпозиции, в точке М3 напряженность

где Н1 и Н2 - напряженности магнитных полей, создаваемые в этой точке токами I1 и I2 соответственно.
Спроецируем данные вектора на ось х, получаем что
Н = Н2 - Н1
Найдем Н1 и Н2, подставляя данные из условия задачи в формулу (1), т.е.
 ;
; 
Тогда


Вычисления:



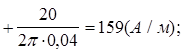


Положительный знак у результирующей напряженности в данной точке говорит о сонаправленности результирующей напряженности с выбранным направлением координатной оси.
Ответ: напряженности магнитного поля, вызванного токами I1 и I2 в точках М1, М2, М3 соответственно равны H1 =120 А/м, Н2 =159 А/м, Н3 =135 А/м.
Задача 72
На рисунке изображены сечения трех прямолинейных бесконечно длинных проводников с токами. Расстояния АВ=ВС =5 см, токи I1 = I2=I и I3 = 2 I. Найти точку на прямой АС, в которой напряженность магнитного поля, вызванного токами I1, I2 и I3, равна нулю.
| Дано: АВ=ВС =5 см I1 = I2=I I3 = 2 I Hрез = 0 | Решение:
Напряженность магнитного поля, создаваемая бесконечно длинным прямолинейным проводником:

|
| х-? | где а - расстояние до данной точки. |
1) Попробуем найти точку, в которой Hрез = 0 в отрезке АВ прямой АВС, свяжем систему координат с точкой местонахождения тока I1, т.е. предположим местонахождение этой точки определяет точка с координатами (х,0).
Согласно принципу суперпозиции

Спроецируем вектора на ось Оу, получаем с учетом того, что Н =0:
 Н2 - Н1 - Н3 = 0
Н2 - Н1 - Н3 = 0
Подставим в данное выражение числовые значения H1, Н2, Н3, сокращая при этом на  , т.к. это отношение не равно нулю. Получаем:
, т.к. это отношение не равно нулю. Получаем:


0,15 х = 0,005,
т.к. (0,1- х)(0,05- х) х ¹ 0
Отсюда
х = 0,033 (м)
Искомая точка удалена от проводника I1 на расстояние х =0,033 м.
2) Предположим, что искомая точка находится на отрезке (¥,А], свяжем систему координат с точкой местонахождения проводника I1, координата точки будет (х, О).
Согласно принципу суперпозиции


Спроецируем вектора на ось Оу, получаем с учетом того, что Н =0:
Н2 - Н1 + Н3 = 0
Подставим в данное выражение числовые значения H1, Н2, Н3, сокращая при этом на  , т.к. это отношение не равно нулю. Получаем:
, т.к. это отношение не равно нулю. Получаем:


-0,15 х = 0,005,
т.к. (0,1+ х)(0,05+ х) х ¹ 0
Отсюда
х = -0,033 (м)
Этот результат подтверждает ранее полученный. Рассматривая две ранее полученные системы координат мы видим, что полученные координаты для точки в этой системе координат совпадает с полученными координатами искомой точки в первом случае, если совмещать две системы.
3) Предположим, что искомая точка находится на отрезке ВС.
 В данном случае векторная сумма не может равняться нулю, т.е.
В данном случае векторная сумма не может равняться нулю, т.е.  , т.к. векторы
, т.к. векторы  ,
, 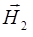 и
и  сонаправлены.
сонаправлены.
4) Предположим, что искомая точка находится на отрезке [С,¥), свяжем систему координат с местонахождением проводника I3 и координата точки будет (х,0).
Согласно принципу суперпозиции

Спроецируем вектора на ось Оу, получаем с учетом того, что Н =0:
Н3 - Н1 - Н2 = 0
Подставим в данное выражение числовые значения H1, Н2, Н3, сокращая при этом на  , т.к. это отношение не равно нулю. Получаем:
, т.к. это отношение не равно нулю. Получаем:


 0,15 х = - 0,01,
0,15 х = - 0,01,
т.к. (0,1+ х)(0,05+ х) х ¹ 0
Отсюда
х = -0,066 (м)
Этот результат подтверждает ранее полученные, т.к. координата полученной точки совпадает с искомой, полученной в первом пункте.
Ответ: точка, в которой напряженность магнитного поля, вызванного токами I1, I2 и I3 равна нулю, находится между точками I1 и I2 на расстоянии а =0,033 м от точки А.
Задача 73
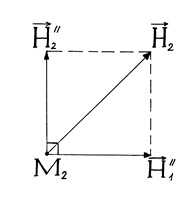
Два прямолинейных бесконечно длинных проводника расположены перпендикулярно друг к другу и находятся во взаимно перпендикулярных плоскостях. Найти напряженности H1 и H2 магнитного поля в точках M1 и M2, если токи I1 =2 А и I2 =3A. Расстояния AM1 = AM2 =l см и АВ = 2см.
| Дано: АВ= 0,02 м I1 = 2 A I2= 3 A AM1 = AM2 =l0-2 м | Решение:
Согласно принципу суперпозиции
 или
или
|
| H1, H2 -? | 
|
1) Найдем напряженность H1 в точке M1.
Векторы напряженности H1 и H2 магнитного поля, вызванного токами I1 и I2 находятся во взаимно перпендикулярных плоскостях.
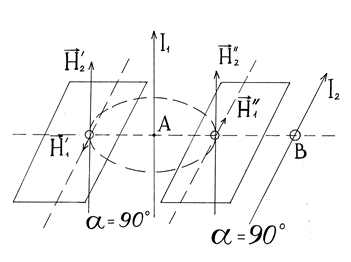 Вектор
Вектор  , является гипотенузой прямоугольного треугольника, у которого катетами являются вектора H1 и H2. Воспользовавшись теоремой Пифагора, найдем
, является гипотенузой прямоугольного треугольника, у которого катетами являются вектора H1 и H2. Воспользовавшись теоремой Пифагора, найдем

Напряженность магнитного поля, созданного бесконечно длинным прямолинейным проводником

где а - расстояние от проводника до рассматриваемой точки.
Воспользовавшись этим выражением, найдем  и
и 


Отсюда


2) Найдем напряженность H2 в точке M2.
Векторы напряженности  и
и  магнитного поля, вызванного токами I1 и I2 находятся во взаимно перпендикулярных плоскостях.
магнитного поля, вызванного токами I1 и I2 находятся во взаимно перпендикулярных плоскостях.
Вектор  является гипотенузой прямоугольного треугольника, у которого катетами являются векторы
является гипотенузой прямоугольного треугольника, у которого катетами являются векторы  и
и  . Воспользовавшись теоремой Пифагора, найдем
. Воспользовавшись теоремой Пифагора, найдем

Воспользовавшись формулой (2), найдем  и
и 


Вычисления:


Ответ: напряженность магнитного поля в точках M1 и M2 соответственно равны Н1 =35,6 А/м и Н2 =57,4 А/м.
Задача 74
Два прямолинейных длинных проводника расположены параллельно на расстоянии а =10 см друг от друга. По проводникам текут токи I1 = I2=5 А в противоположных направлениях. Найти модуль и направление напряженности магнитного поля в точке, находящейся на расстоянии а =10см от каждого проводника.
| Дано: I1 = I2=5 А а = 0,1 м d =0,l м AM1 = AM2 =l0-2 см | Решение:
По определению вектор  перпендикулярен отрезку, связывающему проводник с данной точкой, т.к. вектор перпендикулярен отрезку, связывающему проводник с данной точкой, т.к. вектор  является касательной к является касательной к
|
| H -? | окружности радиусом, равным длине отрезка. |
Согласно принципу суперпозиции

 и
и  - напряженности магнитных полей, созданных бесконечно длинными проводниками I1 и I2.
- напряженности магнитных полей, созданных бесконечно длинными проводниками I1 и I2.
Вектор Н является диагональю параллелограмма со сторонами  и
и  . Воспользовавшись теоремой косинусов, найдем
. Воспользовавшись теоремой косинусов, найдем
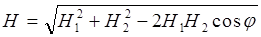 (1)
(1)
где угол j = 60°, т.к. Ð DAC =360°-60°-2×90°=120°, т.к. DАВ¢С¢ - равносторонний, т.к. ÐDAC является прилежащим углом к ÐBCA в параллелограмме ABCD, то ÐBCA=0,5×(360°-240°)=60°
Напряженность магнитного поля, созданного бесконечно длинным проводником:


Используя данную формулу, найдем Н1 и Н2:
 (2)
(2)
 (2)
(2)
Подставим (2), (3) в (1), получаем:

Вычисления:

Ответ: модуль напряженности магнитного поля в точке, находящейся на расстоянии а =10 см от каждого проводника, равна Н =8 А/м. Напряженность магнитного поля направлена перпендикулярно к плоскости, проходящей через оба провода.
Задача 75
Найти напряженность Н магнитного поля, создаваемого отрезком АВ прямолинейного проводника с током в точке С, расположенной на перпендикуляре к середине этого отрезка на расстоянии а =5 см от него. По проводнику течет ток I =20 А. Отрезок АВ проводника виден из точки С под углом 60 градусов.
| Дано: I = 20 А а = 0,05 м a =60° | Решение: Напряженность магнитного поля в точке С, используя закон Био -Савара - Лапласа равна: |
| H -? | 
|
 Из математических соображений
Из математических соображений
l = a·ctga,  ;
; 
Так как

то

Вычисления:
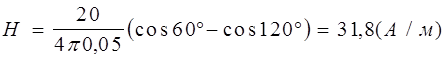
Ответ: напряженность магнитного поля, создаваемого отрезком АВ прямолинейного проводника с током, в точке, расположенной на перпендикуляре к середине этого отрезка на данном расстоянии равна Н =31,8 А/м.
Задача 76
Два круговых витка радиусом R =4 см каждый расположены в параллельных плоскостях на расстоянии а =10 см друг от друга. По виткам текут токи I1 = I2= 1 А. Найти напряженность Н магнитного поля на оси витков в точке, находящейся на равном расстоянии от них. Задачу решить, когда:
а) токи в витках текут в одном направлении;
б) токи в витках текут в противоположных направлениях.
| Дано: R1 = R2 =R= 0,04 м I1 = I2=I = 2 А a = 0 a1 = a2 a) I1 I2 б) I1 ¯ I2 | Решение: а) Рассмотрим случай, когда токи в витках текут в одном направлении. Векторы напряженностей магнитных полей, созданных токами I1 и I2 сонаправлены и направлены в зависимости от циркуляции тока по виткам, согласно принципу суперпозиции |
| H -? |  (1) (1)
|
Учитывая вышесказанное для первого случая
Н = Н1 + Н2
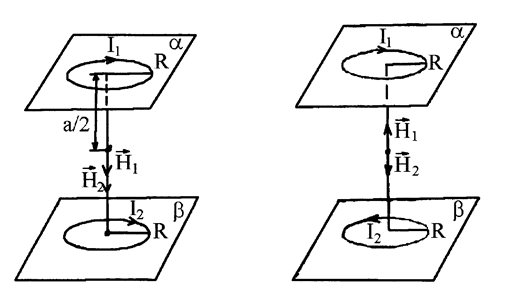 Известно, что напряженность магнитного поля на оси кругового тока
Известно, что напряженность магнитного поля на оси кругового тока
 (2)
(2)
где a1 - расстояние от точки, где ищется напряженность, до плоскости контура; по условию задачи

Подставляя данные из условия в (2), мы видим, что по модулю  и
и 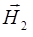 равны, учитывая это условие подставим выражение для Hi и Н1 и Н2 в формулу (1), получаем
равны, учитывая это условие подставим выражение для Hi и Н1 и Н2 в формулу (1), получаем

б) Рассмотрим второй случай, когда токи в витках текут в противоположных направлениях.
Ранее нами было замечено, что векторы  и
и 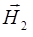 по модулю равны, а как видно из геометрических построений в искомой тоске векторы
по модулю равны, а как видно из геометрических построений в искомой тоске векторы  и
и 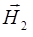 противоположно направлены, а это значит по принципу суперпозиции
противоположно направлены, а это значит по принципу суперпозиции

результирующий вектор будет равен нулю, т.е.
Н1 - Н2 = 0 и Н = 0
Вычисления:

Ответ: напряженность магнитного поля на оси витков в точке, находящейся на равном расстоянии от них, когда:
а) токи в витках текут в одном направлении равна Н =12,2 А/м;
б) токи в витках текут в противоположных направлениях Н =0 А/м.
Задача 77
Ток I =20 А идет по длинному проводнику, согнутому под прямым углом. Найти напряженность Н магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины на расстояние r =10 см.
| Дано: I =20 А r = 0,1 м | Решение: Векторы напряженности магнитных полей, вызванных током I, текущим по отрезкам(-¥;А] и [А;+ ¥) |
| H -? | соответственно находятся на одной прямой перпенди |
 кулярной плоскости, в которой находятся отрезки данного проводника.
кулярной плоскости, в которой находятся отрезки данного проводника.
Напряженность магнитного поля в точке будет равна, с учетом закона Био - Савара - Лапласа

Но
l = a·ctga, 
Далее

Следовательно:
 (1)
(1)
Для первого отрезка, а именно (-¥;А], углы:
a1 =0°,
a2 =45°,
Для второго отрезка, а именно [А;+ ¥), углы:
a1 =45°,
a2 =180°.
Согласно принципу суперпозиции

Так как Н1 Н2 и на одной прямой с Н, то:
Н = Н1 + Н2 (2)
Подставляя (1) в (2), получаем при этом замечая, что а - перпендикуляр, проведенный из точки В на отрезки, для этих отрезков расстояние а одинаково, и может быть найдена по теореме Пифагора из DАВС, учитывая то, что катеты равны по величине и равны а, гипотенуза равна г, отсюда:

Подставляя сначала (3) в (1), потом (1) в (2), получаем

Вычисления:

Ответ: напряженность магнитного поля в точке, лежащей на биссектрисе угла, созданного длинным прямолинейным проводником, и отстоящей от вершины угла на данное расстояние равна Н=13,2A/м.
Задача 78
Из проволоки длиной L =1м сделана квадратная рамка. По рамке течет ток I =10 А. Найти напряженность Н магнитного поля в центре рамки.
| Дано: L =1м I =10 А | Решение:
По условию ABCD - квадрат, значит сторона L рамки будет |
|
|
|


